（新高考地区专用）2021届高考考前冲刺卷 数学（九）

（新高考）2021届高考考前冲刺卷

数 学（九）

注意事项：

1．答题前，先将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。

2．选择题的作答：每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，写在试题卷、草稿纸和答题卡上的非答题区域均无效。

3．非选择题的作答：用签字笔直接答在答题卡上对应的答题区域内。写在试题卷、草稿纸和答题卡上的非答题区域均无效。

4．考试结束后，请将本试题卷和答题卡一并上交。

第Ⅰ卷（选择题）

一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1．设i为虚数单位，则复数的虚部为（    ）

A． B． C． D．

2．已知全集，集合，，则下图阴影部分表示的集合

是（    ）

A． B． C． D．

3．已知，则（    ）

A． B． C． D．

4．已知数列的前项和为，且满足，则（    ）

A．543 B．546 C．1013 D．1022

5．设，，则“”是“”的（    ）

A．充分不必要条件  B．必要不充分条件

C．充要条件  D．既不充分也不必要条件

6．已知的外心为，，，则的值是（    ）

A． B． C． D．

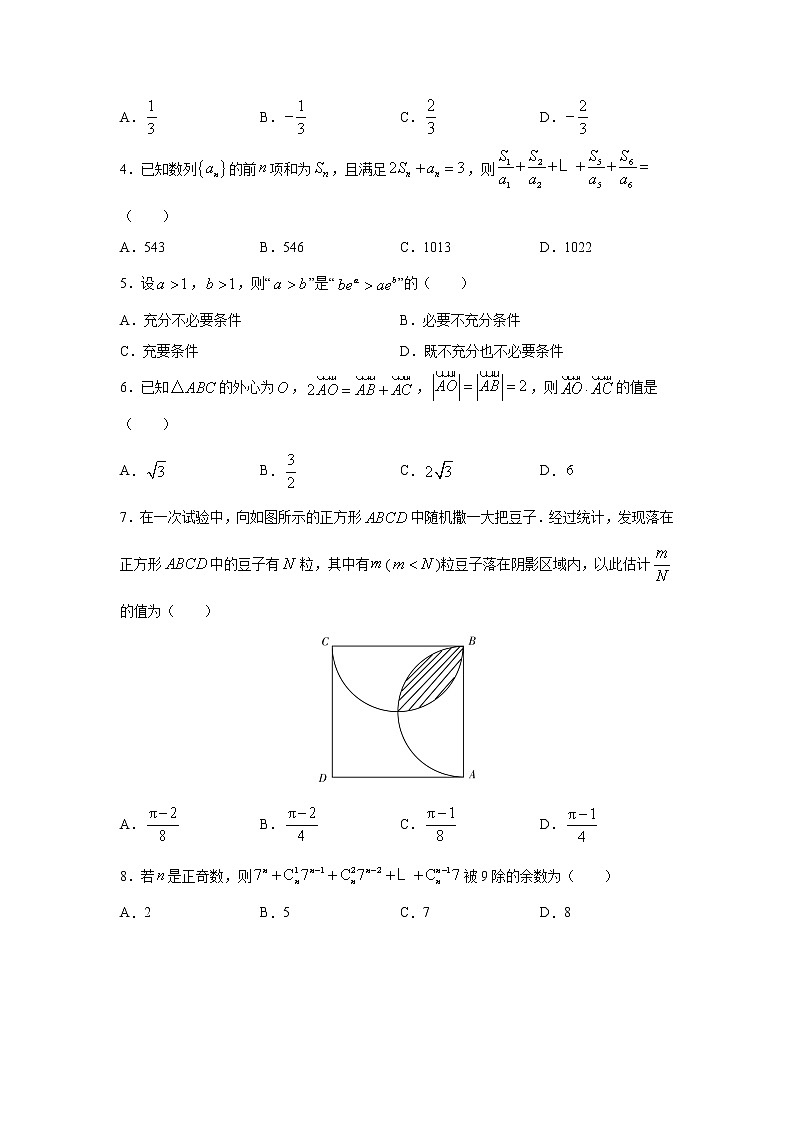
7．在一次试验中，向如图所示的正方形中随机撒一大把豆子．经过统计，发现落在正方形中的豆子有粒，其中有()粒豆子落在阴影区域内，以此估计的值为（    ）

A． B． C． D．

8．若是正奇数，则被9除的余数为（    ）

A．2 B．5 C．7 D．8

二、多项选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．

9．已知，是互不重合的直线，，是互不重合的平面，下列四个命题中正确的是（    ）

A．若，，，，则

B．若，，，则

C．若，，，则

D．若，，，则

10．锐角中三个内角分别是A，B，C且，则下列说法正确的是（    ）

A． B． C． D．

11．以下四个命题表述正确的是（    ）

A．直线恒过定点

B．圆上有且仅有3个点到直线的距离都等于1

C．曲线与曲线恰有三条公切线，则

D．已知圆，点P为直线上一动点，过点向圆引两条切线、，、为切点，则直线经过定点

12．若函数，值域为，则（    ）

A．  B．

C．  D．

第Ⅱ卷（非选择题）

三、填空题：本大题共4小题，每小题5分．

13．曲线在点处的切线方程为__________．

14．如图是一个由正方体截得八面体的平面展开图，它由六个等腰直角三角形和两个正三角形构成，若正三角形的边长为，则这个八面体中有下列结论：

①平面平面；

②多面体是三棱柱；

③直线与直线所成的角为；

④棱所在直线与平面所成的角为．

以上结论正确的是________．

15．已知函数，恰有四个不相等的实数根，，，且满足，则______；的最小值为______．

16．已知、分别为抛物线与圆上的动点，抛物线的焦点为，、为平面内两点，且当取得最小值时，点与点重合；当取得最大值时，点与点重合，则的面积为______．

四、解答题：本大题共6个大题，共70分，解答应写出文字说明、证明过程或演算步骤．

17．（10分）在锐角中，角、，所对的边分别为，，，且．

（1）求证：；

（2）若，求的取值范围．

18．（12分）已知正项数列，其前项和为．

（1）求数列的通项公式；

（2）设，求数列的前项和．

19．（12分）已知四边形是直角梯形，，，，，分别为的中点（如图1），以为折痕把折起，使点到达点的位置且平面平面（如图2）．

（1）求证：平面；

（2）求二面角的余弦值．

20．（12分）已知曲线，与直线．

（1）若直线与曲线相切，求的值；

（2）若直线与曲线交于两点，点，为坐标原点，当为何值时，？

21．（12分）设是给定的正整数（），现有个外表相同的袋子，里面均装有个除颜色外其他无区别的小球，第个袋中有个红球，个白球．现将这些袋子混合后，任选其中一个袋子，并且从中连续取出三个球（每个取后不放回）．

（1）若，假设已知选中的恰为第2个袋子，求第三次取出为白球的概率；

（2）若，求第三次取出为白球的概率；

（3）对于任意的正整数，求第三次取出为白球的概率．

22．（12分）已知函数，，，．

（1）讨论函数的单调性；

（2）当时，若对任意实数，都有函数的图象与直线相切，

求证：．（参考数据：）

1．【答案】B

【解析】，

所以复数的虚部为，故选B．

2．【答案】C

【解析】由图可知阴影部分表示的集合是，

由，得，所以，

由，得，所以，所以或，

所以，故选C．

3．【答案】A

【解析】因为，所以，

即，

则，

故选A．

4．【答案】A

【解析】∵，∴，

两式相减得，即，，

又当时，有，可得，

∴数列是首项为1，公比为的等比数列，

∴，，∴，

∴，

故选A．

5．【答案】C

【解析】设，则，

当时，，

当时，单调递增，

又，，，故选C．

6．【答案】D

【解析】，则，即，

则为的中点，

又因为为的外心，则，

所以为直角三角形，且，如下图所示：

，所以为等边三角形，则，

由勾股定理可得，

，故选D．

7．【答案】A

【解析】设正方形的边长为2，则正方形的面积等于4．

因为阴影部分的面积等于，

所以，故选A．

8．【答案】C

【解析】由题可知：原式

，

因为为正奇数，所以上式可化简为：

，

所以该式除以9，余数为7，故选C．

二、多项选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．

9．【答案】BD

【解析】对于A，若，，，，则与相交或平行，故A错误；

对于B，若，，，则由线面平行的性质得，故B正确；

对于C，若，，，则或，故C错误；

对于D，若，，，则由面面垂直的判定定理得，故D正确，

故选BD．

10．【答案】ACD

【解析】设中三个内角A，B，C分别对的边为，

由正弦定理得，

所以，所以A正确；

因为函数在上为减函数，且，

所以，所以B错误；

在锐角中，因为，所以，

因为函数在上为增函数，所以，即，所以C正确；

同理可得，所以D正确，

故选ACD．

11．【答案】BCD

【解析】对于选项A：由可得：，

由，可得，所以直线恒过定点，故选项A不正确；

对于选项B：圆心到直线的距离等于，圆的半径，

平行于且距离为1的两直线分别过圆心以及和圆相切，

故圆上有且仅有3个点到直线的距离等于，故选项B正确；

对于选项C：由可得，圆心，，

由 可得，

圆心，，由题意可得两圆相外切，所以，

即，解得，故选项C正确；

对于选项D：设点坐标为，所以，即，

因为、分别为过点所作的圆的两条切线，所以，，

所以点在以为直径的圆上，以为直径的圆的方程为，

整理可得，与已知圆相减可得，

消去可得，即，

由，可得，

所以直线经过定点，故选项D正确，

故选BCD．

12．【答案】ACD

【解析】对于A，当，，则恒成立，

所以在上为单调递增函数，因为，故，故选项A正确；

且，故当时，值域为，

对于C，当时，则恒成立，

所以在上单调递减，所以，故，

又的值域为，所以，故，故选项C正确；

对于B，由选项C可知，，故，

所以，，

令，()，

所以，

当时，，则单调递增，

当时，，

此时，故选项B错误；

对于D，设，则，

令，则在恒成立，在上单调递增，

因此时，，，∴是减函数，

又，∴，即，

所以，则D正确，

故选ACD．

第Ⅱ卷（非选择题）

三、填空题：本大题共4小题，每小题5分．

13．【答案】

【解析】，

，，

又，

所求的切线方程为，即，

故答案为．

14．【答案】①③

【解析】

根据平面展开图结合正方体可得如图所示的几何体（如左图所示）．

在正方体中，因为，而平面，平面，

故平面，同理平面，而，

故平面平面，故①正确；

根据棱柱的定义可知，多面体不是三棱柱，故②错误；

因为，且，

故直线与直线所成的角为，故③正确；

因为，故与平面所成的角，即为与平面所成的角，

因为且平面与平面不垂直，

故与平面所成的角小于，故④错误，

故答案为①③．

15．【答案】，

【解析】由解析式可得图象如下图所示：

恰有个不等实根等价于与恰有个不同交点，

由图象可知：，

，，

则，即，

，即，；

关于对称，，

（当且仅当，即时取等号），

当时，，满足与恰有个不同交点，

的最小值为．

16．【答案】

【解析】抛物线的焦点为，圆的标准方程为，

圆心为，半径为，如下图所示：

抛物线的准线为，过点作抛物线的垂线，垂足为点，

由抛物线的定义可得，则，

当时，取最小值，此时取最小值，

直线的方程为，联立，解得，即点，

点到圆上任意一点的距离，当且仅当为射线与圆的交点，且为线段上的点，

所以，，

当且仅当为射线与抛物线的交点，且为射线与圆的交点（为线段上的点），取得最大值．

直线的斜率为，直线的方程为，

联立，解得，即点，

直线的斜率为，直线的方程为，

即，，

点到直线的距离为，因此，，

故答案为．

四、解答题：本大题共6个大题，共70分，解答应写出文字说明、证明过程或演算步骤．

17．【答案】（1）证明见解析；（2）．

【解析】（1）因为，结合余弦定理，

得，即，

由正弦定理得，

所以，所以，

又为锐角三角形，所以，，

所以，即．

（2）由（1）知，所以，

又为锐角三角形，

所以，即，所以，

由正弦定理可知中，

所以．

18．【答案】（1）；（2）．

【解析】（1）由已知，①

所以有，②

②-①，得，即，∴，

所以数列是公比为的等比数列，

又，∴，

所以．

（2）由（1）得，

当n为奇数时，

；

当n为偶数时，

，

综上所述，．

19．【答案】（1）证明见解析；（2）．

【解析】（1）证明：由题意得，，，

由余弦定理得，所以．

如图，连接，易知，于，所以，所以，即，所以．

因为平面平面，平面平面，

所以平面，

又因为平面，所以，

又因为，，平面，所以平面．

（2）解：建立如图所示的空间直角坐标系，

，，，，

，，，

设平面和平面的法向量分别为，，

，令，；

，令，，

所以二面角的余弦值为．

20．【答案】（1）；（2）或．

【解析】（1）设直线与曲线相切于点，

由，则，

所以，解得，所以，即．

将点代入直线的方程，解得．

（2）设，，直线的斜率分别为，．

将代入曲线的方程，整理得，

所以，，

且，即．

①当直线交轴于非负半轴时，若过点，则点三点共线，

显然有，代入直线方程得；

②当直线交轴与负半轴时，若，则，

所以，

代入，解得，

综上所述，或时，．

21．【答案】（1）；（2）；（3）．

【解析】（1）时，第二个袋中有2白2红，共4个球，从中连续取出三个球（每个取后不放回）．

第三次取出为白球的情况有：红红白，红白白，白红白，

∴第三次取出为白球的概率．

（2）设选出的是第个袋，连续三次取球的方法数为，

第三次取出的是白球的三次取球颜色有如下四种情形：

（白，白，白），取法数为，

（白，红，白），取法数为，

（红，白，白），取法数为，

（红，红，白），取法数为，

从而第三次取出的是白球的种数为：

，

则在第个袋子中第三次取出的是白球的概率，

而选到第个袋子的概率为，

故所求概率为．

（3）设选出的是第个袋，连续三次取球的方法数为，

第三次取出的是白球的三次取球颜色有如下四种情形：

（白，白，白），取法数为，

（白，红，白），取法数为，

（红，白，白），取法数为，

（红，红，白），取法数为，

从而第三次取出的是白球的种数为：

，

则在第个袋子中第三次取出的是白球的概率，

而选到第个袋子的概率为，

故所求概率为．

22．【答案】（1）答案见解析；（2）证明见解析．

【解析】（1），

当时，恒成立，函数在上单调递减；

当时，由，得；由，得，

故函数在上单调递减，在上单调递增．

（2）证明：设切点为，则且，

即，，，，

由，得，

设，则，

，得；，得，

故在上单调递减，在上单调递增，

①在单调递增区间上，，故，由，得；

②在单调递减区间上，，，

故在区间上存在唯一的，使得，故，

此时由，得，

函数在上递增，

，，故，

综上所述，