




人教B版 (2019)必修 第四册9.2 正弦定理与余弦定理的应用说课ppt课件
展开蜂窝是大自然最奇妙的建筑之一,它排列形状极有规则,所有的蜂窝都是六边形.六边形像三角形一样有稳定性,因而蜜蜂在建窝时为了使其更稳定,便建成六边形.更使人惊讶的是法国科学家马拉尔的发现,马拉尔通过对蜂窝的多年研究,发现所有蜂窝的钝角都是109°28',所有的锐角都是70°32'.这不能不说是蜜蜂建筑的奇迹.那么当你研究蜂窝的特征时,需要什么数学知识呢?
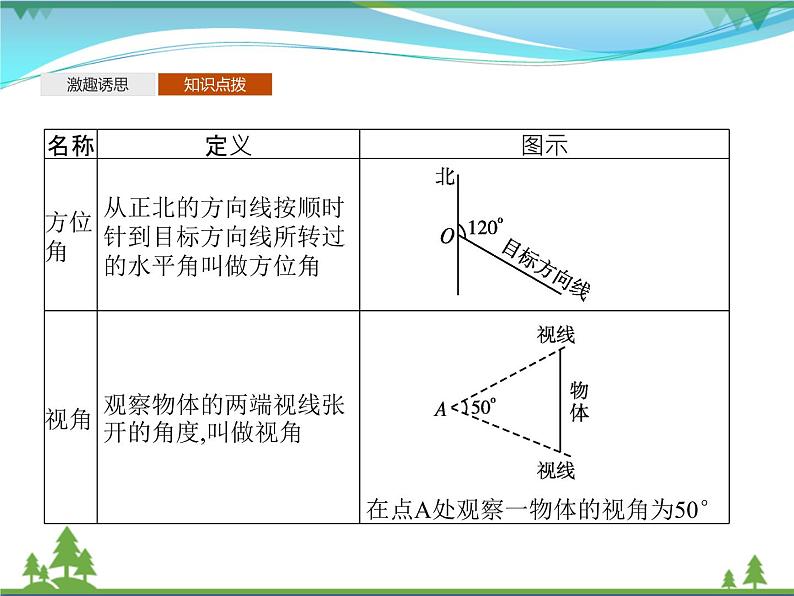
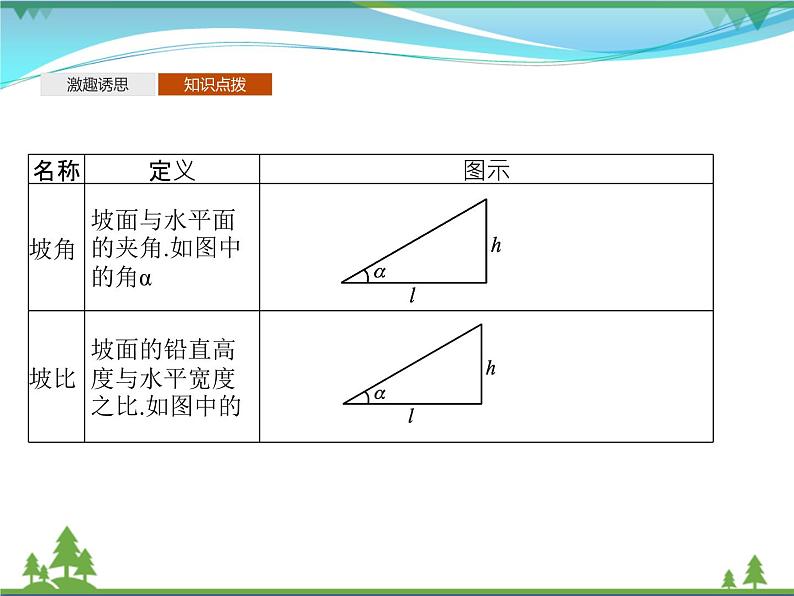
知识点一:测量中的基本术语
微练习1若P在Q的北偏东44°50'方向上,则Q在P的( )A.东偏北45°50'方向上B.北偏东45°50'方向上C.南偏西44°50'方向上D.西偏南45°50'方向上答案:C解析:如图所示,点Q在点P的南偏西44°50'的方向上.故选C.
微练习2从A处望B处的仰角为α,从B处望A处的俯角为β,则α,β的关系为( )A.α>β B.α=βC.α+β=90°D.α+β=180°答案:B解析:根据题意和仰角、俯角的概念,得α=β,故选B.
微练习3已知目标A的方位角为135°,请画出其图示.
微练习4请分别画出北偏东30°,南偏东45°的方向角.
知识点二:解三角形应用题1.解题思路
2.基本步骤运用正弦定理、余弦定理解决实际问题的基本步骤如下:①分析:理解题意,弄清已知与未知,画出示意图(一个或几个三角形);②建模:根据已知条件与求解目标,把已知量与待求量尽可能地集中在有关三角形中,建立一个解三角形的数学模型;③求解:利用正弦定理、余弦定理解三角形,求得数学模型的解;④检验:检验所求的解是否符合实际问题,从而得出实际问题的解.
名师点析 1.解三角形应用问题常见的几种情况解三角形应用题经抽象概括为解三角形问题时,常有以下几种情况:(1)已知量与未知量全部集中在一个三角形中,可直接用正弦定理或余弦定理求解;(2)已知量与未知量涉及两个或两个以上三角形时,可先解条件充足的三角形,然后逐步求解其他三角形,有时需要设出未知量,从几个三角形中列方程(组),通过解方程(组)得出所求的解.
2.求解模型的解时应该注意的问题在求模型的解时,为避免误差的积累,尽可能用原始数据,少用间接求出的量,要根据求解问题对精确度的要求合理地选择近似值,要注意实际问题中是否有一些特殊三角形,如等边三角形、直角三角形、等腰三角形等,以优化解题过程,如果将正弦定理、余弦定理看成是几个“方程”的话,那么解三角形应用题的实质就是把已知量按方程思想进行处理,解题时应根据已知量和未知量,选择一个比较容易解的方程,从而使解题过程简捷.
微思考1距离问题的处理方法是什么?
提示:①测量从一个可到达的点A到一个不可到达的点B之间的距离问题.如图所示.这实际上就是已知三角形的两个角和一边解三角形的问题,用正弦定理就可解决.
②测量两个不可到达的点A,B之间的距离问题.如图所示.
首先把求不可到达的两点A,B之间的距离转化为应用余弦定理求三角形的边长问题,然后把求B,C和A,C的距离问题转化为测量可到达的一点与不可到达的一点之间的距离问题.
微思考2高度问题的处理方法是什么?
提示:①测量底部不可到达的建筑物的高度时,由于底部不可到达,这类问题不能直接用解直角三角形的方法解决,但常用正弦定理或余弦定理计算出建筑物顶部或底部到一个可到达的点之间的距离,然后转化为解直角三角形的问题.②在测量底部不可到达的建筑物的高度时,可以借助正弦定理或余弦定理,构造两角(两个仰角或两个俯角)和一边或三角(两个方向角和仰角)和一边,如下图.
微思考3角度问题的处理方法是什么?
提示:测量角度问题主要是指在海上或空中测量角度的问题,如确定目标的方位,观察某一建筑物的视角等.解决它们的关键是根据题意和图形及有关概念,确定所求的角在哪个三角形中,该三角形中已知哪些量,需要求哪些量.通常是根据题意,从实际问题中抽象出一个或几个三角形,然后通过解这些三角形,得到所求的量,从而得到实际问题的解.解题时应认真审题,结合图形去选择定理,这是最关键、最重要的一步.
微练习如图,某船开始航行时,灯塔在该船北偏东30°方向,后来该船沿北偏东60°的方向航行60海里,此时灯塔在正西方向,则此时船与灯塔的距离是( )A.30海里 B.60海里
测量高度问题例1如图所示,在山顶铁塔上B处测得地面上一点A的俯角为α,在塔底C处测得A处的俯角为β.已知铁塔BC部分的高为h,求山高CD.
反思感悟 求高度(距离)问题应注意的两点(1)根据题意,如果没有图形,先画出示意图,然后选定或确定所求量所在的三角形,若其他量已知,则直接求解;若有未知量,则先把未知量放在另一确定三角形中求解.(2)确定用正弦定理还是余弦定理,如果都有可能,则选择更便于计算的定理.当题目中出现互补(余)的角时,注意补角(余角)之间的关系.
变式训练 1在飞机上,某一时刻测得地面上两建筑物的俯角分别为45°和30°,这一时刻飞机对两建筑物的视角为45°.若两建筑物之间的距离为2 km,则飞机的飞行高度为 .
解析:设两建筑物为A,B,这一时刻飞机所在位置为P,其在地面上的投影为D,则由题意知,∠PAD=30°,∠PBD=45°,∠APB=45°,设飞机飞行高度为h,所以 由余弦定理得AB2=PA2+PB2-2PA·PBcs∠APB,所以8=4h2+2h2-4h2=2h2,所以h=2 km.
例2如图所示,当甲船位于A处时,获悉在其正东方向相距20 n mile的B处有一艘渔船遇险等待营救.甲船立即前往救援,同时把消息告知在甲船南偏西30°,相距10 n mile的C处的乙船,试问乙船应朝北偏东多少度的方向沿直线前往B处救援
解:如图所示,连接CB.在△ABC中,∠CAB=90°+30°=120°.由余弦定理,得BC2=AB2+AC2-2AB×AC×cs 120°.又AC=10,AB=20,得
又∠ACB为锐角,所以∠ACB≈41°.作CM⊥BA,交BA的延长线于点M,则∠BCM=30°+∠ACB≈71°.所以乙船应朝北偏东约71°的方向沿直线前往B处救援.
反思感悟 解答角度问题的解决策略解决这类问题一定要搞清方向角,画出符合题意的图形,将所给距离和角度标在图中,然后分析可解的三角形及其与待求角的关系,确定解题步骤.
变式训练 2缉私巡逻艇在一小岛A南偏西50°的方向,距小岛A 12 n mile的B处,发现隐藏在小岛A边上的一走私船正开始向小岛A北偏西10°方向行驶,测得其速度为每小时10 n mile,问巡逻艇需用多大的速度朝什么方向航行才能恰在两个小时后截获该走私船?(参考数据:sin 38°≈0.62)
解:如右图所示,AC所在射线即走私船航行路线,假设巡逻艇在C处截获走私船,巡逻艇的速度为每小时x n mile,则BC=2x,AC=20.依题意∠BAC=180°-50°-10°=120°,
而如图所示的Rt△ADB中,∠ABD=40°.所以∠EBC=90°-38°-40°=12°.即巡逻艇用每小时14 n mile的速度向北偏东12°的方向航行.
正弦定理、余弦定理在力学中的应用例3如图,在墙上有一个三角形支架OAB,吊着一个重力为12 N的灯,OA,OB都是轻杆,只受沿杆方向的力,试求杆OA,OB所受力的大小.
反思感悟 解答力学问题的解决策略解答与力学有关的三角形问题,要抓住力的方向与大小和受力平衡的关系,准确进行受力分解.
变式训练 3作用在小车A上的两个水平力F1,F2,|F1|=40 N,|F2|=20 N,夹角为60°,小车的摩擦力大小为20 N,则小车在力的作用下能否保持静止?
解:如图所示.在▱ABCD中,由题意AB=20,AD=BC=40,∠ABC=120°,在△ABC中,由余弦定理,得
探究距离测量问题【角度一】 两点不相通的距离典例1如图所示,要测量一水塘两侧A,B两点间的距离,其方法先选定适当的位置C,用经纬仪测出角α,再分别测出AC,BC的长b,a,则可求出A,B两点间的距离.即AB= .若测得CA=400 m,CB=600 m,∠ACB=60°,试计算AB长.
解:在△ABC中,由余弦定理得AB2=AC2+BC2-2AC·BCcs∠ACB,所以AB2=4002+6002-2×400×600cs 60°=280 000.所以
【角度二】两点间可视但有一点不可到达典例2如图所示,A,B两点在一条河的两岸,测量者在点A的同侧,且点B不可到达,要测出AB的长度,其方法是在点A所在的岸边选定一点C,可以测出AC的距离m,再借助仪器,测出∠ACB=α,∠CAB=β,在△ABC中,运用正弦定理就可以求出AB.若测出AC=60 m,∠BAC=75°,∠BCA=45°,则A,B两点间的距离为 .
【角度三】 两点都不可到达典例3如图,A,B两点在河的同侧,且A,B两点均不可到达,要测出AB的距离,其测量者可以在河岸边选定两点C,D,测得CD=a,同时在C,D两点分别测得∠BCA=α,∠ACD=β,∠CDB=γ,∠BDA=δ.在△ADC和△BDC中,由正弦定理分别计算出AC和BC,再在△ABC中,应用余弦定理计算出AB.
2.(2020天津一中高一期末)雕塑是大学校园不可分割的一部分,有些甚至能成为这个大学的象征,在中国科学技术大学校园中就有一座郭沫若的雕像.雕像由像体AD和底座CD两部分组成.如图,在Rt△ABC中,∠ABC=70.5°,在Rt△DBC中,∠DBC=45°,且CD=2.3米,则像体AD的高度为( )(最后结果精确到0.1米,参考数据:sin 70.5°≈0.943,cs 70.5°≈0.334,tan 70.5°≈2.824)
A.4.0米B.4.2米C.4.3米D.4.4米
3.一艘轮船按照北偏西30°的方向以每小时21海里的速度航行,一个灯塔M原来在轮船的北偏东30°的方向,经过40分钟后,测得灯塔在轮船的北偏东75°的方向,则灯塔和轮船原来的距离是 海里.
解析:如图所示:M为灯塔,C为轮船,∠MBC=180°-75°-30°=75°,
4.甲船在A处发现乙船在北偏东60°的B处,乙船正以a n mile/h的速度向北行驶.已知甲船的速度是 a n mile/h,则甲船应沿着 方向前进,才能最快与乙船相遇?
解析:如图,设经过t h两船在点C相遇,
因为0°<∠CAB<90°,所以∠CAB=30°,所以∠DAC=60°-30°=30°.即甲船应沿北偏东30°的方向前进,才能最快与乙船相遇.
5.要测量对岸两点A,B之间的距离,工作人员选取了相距200 m的C,D两点,并测得∠ADC=105°,∠BDC=15°,∠BCD=120°,∠ACD=30°,求A,B两点之间的距离.
人教B版 (2019)必修 第四册第九章 解三角形9.2 正弦定理与余弦定理的应用教课内容课件ppt: 这是一份人教B版 (2019)必修 第四册第九章 解三角形9.2 正弦定理与余弦定理的应用教课内容课件ppt,共36页。
高中数学人教B版 (2019)必修 第四册9.2 正弦定理与余弦定理的应用教学演示ppt课件: 这是一份高中数学人教B版 (2019)必修 第四册9.2 正弦定理与余弦定理的应用教学演示ppt课件,共22页。PPT课件主要包含了复习回顾,问题1测量相关术语,方向角,某偏某多少度,问题2高度问题,问题2距离问题,问题3几何类问题等内容,欢迎下载使用。
人教B版 (2019)必修 第四册9.2 正弦定理与余弦定理的应用教学演示课件ppt: 这是一份人教B版 (2019)必修 第四册9.2 正弦定理与余弦定理的应用教学演示课件ppt,共25页。PPT课件主要包含了学习目标,概念解析,顺时针,0°360°,情境与问题,例题解析,当堂达标,课堂小结等内容,欢迎下载使用。













