





- 人教B版(2019)高中数学必修第四册第十一章立体几何初步11.4.1直线与平面垂直 课件(共139张PPT) 课件 0 次下载
- 人教B版(2019)高中数学必修第四册第十一章立体几何初步11.1.5旋转体 同步刷题 课件(共46张PPT) 课件 0 次下载
- 人教B版(2019)高中数学必修第四册第十一章立体几何初步11.3.3平面与平面平行 同步刷题 课件(共35张PPT) 课件 0 次下载
- 人教B版(2019)高中数学必修第四册第十一章第一章11.1.1空间几何体与斜二测画法刷题课件(共21张PPT) 课件 0 次下载
- 人教B版(2019)高中数学必修第四册第十一章立体几何初步11.2平面的基本事实与推论 同步刷题 课件(共18张PPT) 课件 0 次下载
数学必修 第四册11.4.2 平面与平面垂直课文配套课件ppt
展开1.(多选)下列命题正确的是( )A.两个相交平面组成的图形叫做二面角B.异面直线a,b分别和一个二面角的两个面垂直,则a,b所成的角与这个二面角相等或互补C.二面角的平面角是从棱上一点出发,分别在两个面内作射线所成角的最小角D.二面角的大小与其平面角的顶点在棱上的位置没有关系
对于A,显然混淆了平面与半平面的概念,是错误的;对于B,因为a,b分别垂直于两个面,所以也垂直于二面角的棱,但由于异面直线所成的角为锐角或直角,所以应是相等或互补,是正确的;对于C,因为所作射线不一定垂直于棱,所以是错误的;D是正确的.故选BD.
11.4.2 平面与平面垂直 刷基础
2.从空间一点P向二面角α-l-β的两个面α,β分别作垂线PE,PF,E,F为垂足.若∠EPF=60°,则二面角的平面角的大小是( )A.60° B.120° C.60°或120° D.不确定
若点P在二面角内,则二面角的平面角为120°;若点P在二面角外,则二面角的平面角为60°.
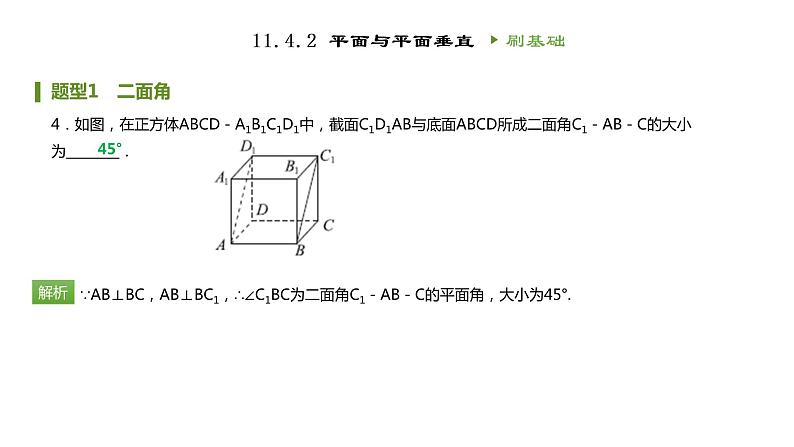
4.如图,在正方体ABCD-A1B1C1D1中,截面C1D1AB与底面ABCD所成二面角C1-AB-C的大小为________.
∵AB⊥BC,AB⊥BC1,∴∠C1BC为二面角C1-AB-C的平面角,大小为45°.
题型2 面面垂直的判定
5.在正四面体PABC中,D,E,F分别是AB,BC,CA的中点,下面四个结论中不成立的是( )A.BC∥平面PDF B.DF⊥平面PAEC.平面PAE⊥平面ABC D.平面PDE⊥平面ABC
如图,因为BC∥DF,所以BC∥平面PDF.由正四面体的性质知BC⊥PE,BC⊥AE,所以BC⊥平面PAE,所以DF⊥平面PAE,平面PAE⊥平面ABC.
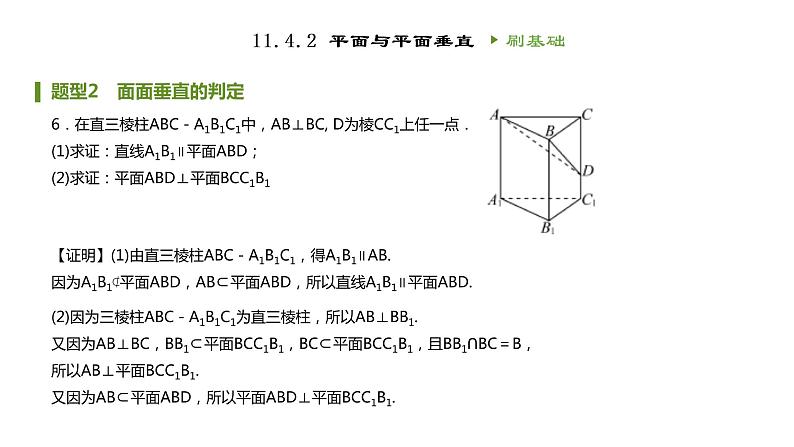
6.在直三棱柱ABC-A1B1C1中,AB⊥BC, D为棱CC1上任一点.(1)求证:直线A1B1∥平面ABD;(2)求证:平面ABD⊥平面BCC1B1
【证明】(1)由直三棱柱ABC-A1B1C1,得A1B1∥AB.因为A1B1⊄平面ABD,AB⊂平面ABD,所以直线A1B1∥平面ABD.
(2)因为三棱柱ABC-A1B1C1为直三棱柱,所以AB⊥BB1.又因为AB⊥BC,BB1⊂平面BCC1B1,BC⊂平面BCC1B1,且BB1∩BC=B,所以AB⊥平面BCC1B1.又因为AB⊂平面ABD,所以平面ABD⊥平面BCC1B1.
题型3 面面垂直的性质
7.若平面α⊥平面β,平面β⊥平面γ,则( )A.α∥γ B.α⊥γC.α与γ相交但不垂直 D.以上都有可能
以正方体为模型:相邻两侧面都与底面垂直;相对的两侧面都与底面垂直;一侧面和一对角面都与底面垂直.故选D.
8.若平面α⊥平面β,且平面α内的一条直线a垂直于平面β内的一条直线b,则( )A.直线a必垂直于平面βB.直线b必垂直于平面α C.直线a不一定垂直于平面βD.过a的平面与过b的平面垂直
设α∩β=l.∵α⊥β,a⊂α,b⊂β,a⊥b,∴当a∥l时,b⊥α;当b∥l时,a⊥β,其他情况下未必有b⊥α或a⊥β.
9.设α,β是两个不同的平面,l是一条直线,以下叙述正确的是( )A.若l⊥α,α⊥β,则l⊂β B.若l∥α,α∥β,则l⊂βC.若l⊥α,α∥β,则l⊥β D.若l∥α,α⊥β,则l⊥β
l⊥α,α⊥β⇒l∥β或l⊂β,A错;l∥α,α∥β⇒l∥β或l⊂β,B错;l⊥α,α∥β⇒l⊥β,C正确;若l∥α,α⊥β,则l与β的位置关系不确定,D错.
10.已知长方体ABCD-A1B1C1D1,在平面AA1B1B上任取一点M,作ME⊥AB于点E,则( )A.ME⊥平面ABCD B.ME⊂平面ABCDC.ME∥平面ABCD D.以上都有可能
∵ME⊂平面AA1B1B,平面AA1B1B∩平面ABCD=AB,且平面AA1B1B⊥平面ABCD,ME⊥AB,∴ME⊥平面ABCD.
11.如图,在斜三棱柱ABC-A1B1C1中,∠BAC=90°,BC1⊥AC,则点C1在底面ABC上的射影点H必在 ( )A.直线AB上 B.直线BC上C.直线AC上 D.△ABC内部
连接AC1.∵AC⊥AB,AC⊥BC1,∴AC⊥平面ABC1.又∵AC⊂平面ABC,∴平面ABC1⊥平面ABC,∴点C1在平面ABC上的射影点H必在平面ABC1与平面ABC的交线AB上,故选A.
题型4 平行垂直关系的综合问题
12.如果直线l,m与平面α,β,γ满足l=β∩γ,l∥α,m⊂α,m⊥γ,那么必有( )A.α⊥γ和l⊥m B.α∥γ和m∥βC.m∥β且l⊥m D.α∥β和α⊥γ
∵m⊂α,m⊥γ,∴α⊥γ.∵m⊥γ,β∩γ=l,∴m⊥l,故选A.
13.设a,b是互不垂直的两条异面直线,则下列命题成立的是( )A.存在唯一直线l,使得l⊥a,且l⊥bB.存在唯一直线l,使得l∥a,且l⊥bC.存在唯一平面α,使得a⊂α,且b∥αD.存在唯一平面α,使得a⊂α,且b⊥α
过直线a上任意一点P,作b的平行线c,由a,c相交确定一个平面α.直线l只需垂直于平面α,就会与b垂直,这样的直线有无数条,故A错误.根据平面两条直线所成角的定义,排除B.根据线面垂直的概念,排除D.所以选C.
14.(多选)已知m,n表示两条不同的直线,α表示平面,下列说法错误的是( )A.若m∥α,n∥α,则m∥nB.若m⊥α,m⊥n,则n∥αC.若m⊥α,n⊂α,则m⊥nD.若m∥α,m⊥n,则n⊥α
如图,在正方体ABCD-A′B′C′D′中,令底面A′B′C′D′=α.对于A,令m=AB,n=BC,满足m∥α,n∥α,但m∥n不成立,故错误;对于B,令m=AA′,n=A′B′,满足m⊥α,m⊥n,但n∥α不成立,故错误;对于D,令m=AB,n=AD,满足m∥α,m⊥n,但n⊥α不成立,故错误.故选ABD.
15.给出下列命题:①a⊥α,b⊂α⇒a⊥b;②a⊥α,a∥b⇒b⊥α;③a⊥α,b∥α⇒a⊥b;④a⊥b,a⊥c,b⊂α,c⊂α⇒a⊥α;⑤a∥α,a⊥b⇒b⊥α;⑥a⊥α,b⊥a⇒b∥α.其中真命题的个数是( )A.3 B.4 C.5 D.6
因为a⊥α,所以a垂直于平面α内的任意直线,所以①正确.若两条平行线中的一条直线与一个平面垂直,则另一条直线也与这个平面垂直,所以②正确.由线面垂直,线线、线面平行的性质知,若a⊥α,b∥α,则a⊥b,所以③正确.由线面垂直的判定定理可知,④不正确.当a∥α,a⊥b时,b可能与α平行、垂直、斜交或b在α内,所以⑤不正确.当a⊥α,b⊥a时,b可能与α平行,b也可能在α内,故⑥不正确.
1.空间四边形ABCD中,若AD⊥BC,BD⊥AD,则有( )A.平面ABC⊥平面ADC B.平面ABC⊥平面ADBC.平面ABC⊥平面DBC D.平面ADC⊥平面DBC
∵AD⊥BC,AD⊥BD,BC∩BD=B,∴AD⊥平面DBC.又∵AD⊂平面ADC,∴平面ADC⊥平面DBC.
11.4.2 平面与平面垂直 刷提升
2.已知直线m,n和平面α,β,若α⊥β,α∩β=m,n⊂α,要使n⊥β,则应增加的条件是( )A.m∥n B.n∥α C.n⊥m D.n⊥α
由平面与平面垂直的性质定理可知,要使n⊥β,只需在α⊥β,α∩β=m,n⊂α上增加条件n⊥m,故选C.
3.若l为一条直线,α,β,γ为三个互不重合的平面,给出下面三个结论:①α⊥γ,β⊥γ⇒α⊥β;②α⊥γ,β∥γ⇒α⊥β;③l∥α,l⊥β⇒α⊥β.其中正确的结论有( )A.0个 B.1个 C.2个 D.3个
结论②③正确,①中α,β可能平行,也可能相交.
4.如图,设P是正方形ABCD所在平面外一点,且PA⊥平面ABCD,则平面PAB与平面PBC、平面PAD的位置关系是( )A.平面PAB与平面PBC、平面PAD都垂直B.它们两两垂直C.平面PAB与平面PBC垂直,与平面PAD不垂直D.平面PAB与平面PBC、平面PAD都不垂直
∵PA⊥平面ABCD,∴PA⊥BC.又∵BC⊥AB,PA∩AB=A,∴BC⊥平面PAB.∵BC⊂平面PBC,∴平面PBC⊥平面PAB.∵AD⊥PA,AD⊥AB,PA∩AB=A,∴AD⊥平面PAB.∵AD⊂平面PAD,∴平面PAD⊥平面PAB.由已知易得平面PBC与平面PAD不垂直,故选A.
5.在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°.将△ABD沿BD折起,使平面ABD⊥平面BCD,构成三棱锥A-BCD,如图.则在三棱锥A-BCD中,下列结论正确的是 ( )A.平面ABD⊥平面ABCB.平面ADC⊥平面BDCC.平面ABC⊥平面BDCD.平面ADC⊥平面ABC
在平面图形中,CD⊥BD,折起后仍然满足CD⊥BD.因为平面ABD⊥平面BCD,所以CD⊥平面ABD,CD⊥AB.又因为AB⊥AD,所以AB⊥平面ADC,所以平面ADC⊥平面ABC.
6.若四边形ABCD是正方形,PA⊥平面ABCD,则在平面PAB、平面PBC、平面PCD、平面PDA和平面ABCD中,互相垂直的平面一共有________对.
互相垂直的平面有平面PAB和平面ABCD,平面PBC和平面PAB,平面PCD和平面PDA,平面PDA和平面ABCD,平面PAB和平面PDA,共5对.
7.如图,若边长为4和3与边长为4和2的两个矩形所在的平面互相垂直,则cs α∶cs β=________.
8.如图,四面体P-ABC中,PA=PB=13,平面PAB⊥平面ABC,∠ACB=90°,AC=8,BC=6,则PC=________.
易错点1 对面面垂直的判定定理理解不到位致误
10.(多选)如图,点P在正方体ABCD-A1B1C1D1的面对角线BC1上运动,则下面四个结论中,正确的有( )A.三棱锥A-D1PC的体积不变 B.A1P∥平面ACD1 C.DP⊥BC1 D.平面PDB1⊥平面ACD1
连接AC,A1C1,A1B,AD1,D1C.因为AA1∥CC1,AA1=CC1,所以四边形AA1C1C是平行四边形,所以AC∥A1C1.又因为AC⊄平面A1BC1,A1C1⊂平面A1BC1,所以AC∥平面A1BC1.同理可证AD1∥平面A1BC1,又因为AC⊂平面ACD1,AD1⊂平面ACD1,且AC∩AD1=A,所以平面ACD1∥平面A1BC1.因为A1P⊂平面A1BC1,所以A1P∥平面ACD1,故B正确.因为BC1∥AD1,所以BC1∥平面ACD1,所以点P到平面ACD1的距离不变.又因为VA-D1PC=VP-ACD1,所以三棱锥A-D1PC的体积不变,故A正确.连接DB,DC1,DP.因为DB=DC1,所以当P为BC1的中点时才有DP⊥BC1,故C错误.
11.4.2 平面与平面垂直 刷易错
因为BB1⊥平面ABCD,AC⊂平面ABCD,所以AC⊥BB1.又因为AC⊥BD,BB1∩BD=B,所以AC⊥平面BB1D1D.连接B1D,又因为B1D⊂平面BB1D1D,所以B1D⊥AC.同理可证B1D⊥AD1.又因为AC⊂平面ACD1,AD1⊂平面ACD1,AC∩AD1=A,所以B1D⊥平面ACD1.又因为B1D⊂平面PDB1,所以平面PDB1⊥平面ACD1,故D正确.
易错点2 对面面垂直的性质应用不当致误
11.如图,在四棱锥P-ABCD中,AB∥CD,AB⊥AD,CD=2AB,平面PAD⊥底面ABCD,PA⊥AD,E和F分别是CD和PC的中点.求证:(1)PA⊥底面ABCD;(2)BE∥平面PAD;(3)平面BEF⊥平面PCD.
【证明】(1)∵平面PAD⊥底面ABCD,平面PAD∩底面ABCD=AD,PA⊂平面PAD,PA⊥AD,∴PA⊥底面ABCD.
(2)∵AB∥CD,CD=2AB,E是CD的中点,∴AB∥DE,且AB=DE.∴四边形ABED为平行四形.∴BE∥AD.又∵BE⊄平面PAD,AD⊂平面PAD,∴BE∥平面PAD.
(3)∵AB⊥AD,四边形ABED为平行四边形,∴BE⊥CD,AD⊥CD.由(1)知PA⊥底面ABCD,∴PA⊥CD.∵PA∩AD=A,∴CD⊥平面PAD.∴CD⊥PD.∵E和F分别是CD和PC的中点,∴PD∥EF,∴CD⊥EF.∵CD⊥BE,EF∩BE=E,∴CD⊥平面BEF.∵CD⊂平面PCD,∴平面BEF⊥平面PCD.
人教B版 (2019)必修 第四册11.4.2 平面与平面垂直背景图ppt课件: 这是一份人教B版 (2019)必修 第四册11.4.2 平面与平面垂直背景图ppt课件,共29页。
高中数学人教B版 (2019)必修 第四册第十一章 立体几何初步11.4 空间中的垂直关系11.4.2 平面与平面垂直课文内容ppt课件: 这是一份高中数学人教B版 (2019)必修 第四册第十一章 立体几何初步11.4 空间中的垂直关系11.4.2 平面与平面垂直课文内容ppt课件,共32页。PPT课件主要包含了学习目标,半平面,两个半平面,温故知新,平面角,性质定理,一个平面内,典例解析,归纳总结,跟踪训练等内容,欢迎下载使用。
高中数学人教B版 (2019)必修 第四册11.4.2 平面与平面垂直备课ppt课件: 这是一份高中数学人教B版 (2019)必修 第四册11.4.2 平面与平面垂直备课ppt课件,共32页。PPT课件主要包含了学习目标,2图形语言,尝试与发现,二面角,情境与问题,半平面,两个半平面,概念解析,概念辨析,典例解析等内容,欢迎下载使用。













