

2021年广东省佛山市顺德区中考数学一模试卷
展开2021年广东省佛山市顺德区中考数学一模试卷
一、选择题(10个题,每题3分,共30分)
1.(3分)2020年,我国脱贫攻坚战取得了全面胜利,现行标准下的9899万农村贫困人口全部脱贫,其中9899万用科学记数法表示为( )
A.989.9×105 B.98.99×106 C.9.899×107 D.0.9899×108
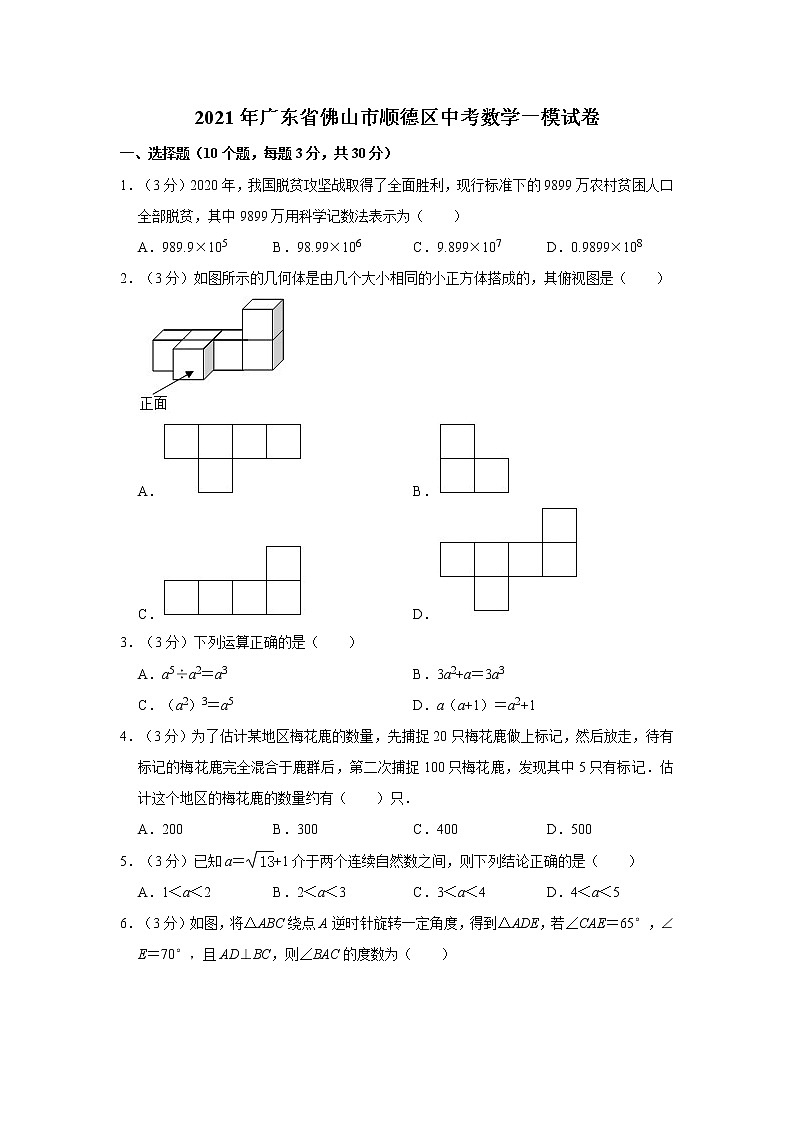
2.(3分)如图所示的几何体是由几个大小相同的小正方体搭成的,其俯视图是( )
A. B.
C. D.
3.(3分)下列运算正确的是( )
A.a5÷a2=a3 B.3a2+a=3a3
C.(a2)3=a5 D.a(a+1)=a2+1
4.(3分)为了估计某地区梅花鹿的数量,先捕捉20只梅花鹿做上标记,然后放走,待有标记的梅花鹿完全混合于鹿群后,第二次捕捉100只梅花鹿,发现其中5只有标记.估计这个地区的梅花鹿的数量约有( )只.
A.200 B.300 C.400 D.500
5.(3分)已知a=+1介于两个连续自然数之间,则下列结论正确的是( )
A.1<a<2 B.2<a<3 C.3<a<4 D.4<a<5
6.(3分)如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE,若∠CAE=65°,∠E=70°,且AD⊥BC,则∠BAC的度数为( )
A.60° B.85° C.75° D.90°
7.(3分)如图,E是平行四边形ABCD边AD延长线上一点,且DE=AD,连接BE、CE、BD.若AB=BE,则四边形BCED是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
8.(3分)如图,一次函数y=x+1的图象与反比例函数y=的图象的一个交点为A(2,m),则不等式>3的解集是( )
A.x>2 B.0<x<2
C.x>0 D.x<﹣3或0<x<2
9.(3分)如图,AB为⊙O的直径,C、D为⊙O上两点,∠BCD=30°,BD=2,则AB的长度为( )
A.3 B.4 C.5 D.6
10.(3分)若关于x的不等式组有且只有8个整数解,关于y的方程=1的解为非负数,则满足条件的整数a的值为( )
A.﹣8 B.﹣10
C.﹣8或﹣10 D.﹣8或﹣9或﹣10
二、填空题(7个题,每题4分,共28分)
11.(4分)因式分解:x2﹣16= .
12.(4分)若关于x的一元二次方程x2﹣2x+c=0没有实数根.则实数c取值范围是 .
13.(4分)一个正多边形的每个内角都是144°,则这个多边形的内角和为 .
14.(4分)在边长为2的正方形ABCD中,点E是AB的中点,EF⊥BD于点F,则EF的长度 .
15.(4分)某校组织了一次初三科技小制作比赛,有A、B、C、D四个班共提供了100件参赛作品.C班提供的参赛作品的获奖率为50%,其它几个班的参赛作品情况及获奖情况绘制在图1和图2两幅尚不完整的统计图中,则获奖率最高的班级是 .
16.(4分)如图,在A点有一个热气球,由于受西风的影响,以20米/分的速度沿与地面成75°角的方向飞行,10分钟后到达C处,此时热气球上的人测得地面上的B点俯角为30°,则A、B两点间的距离为 米.
17.(4分)如图,在四边形ABCD中,AB=CB,AD=CD.若∠ABD=∠ACD=30°,AD=1,则△ABC的内切圆面积 (结果保留π).
三、解答题(一)(3个题,每题6分,共18分)
18.(6分)计算:2cos30°﹣()﹣2++|1﹣|.
19.(6分)先化简,再计算:(+)÷,其中x满足x2﹣2x+2=0.
20.(6分)如图,M是⊙O的半径OA的中点,弦BC⊥AO于点M,过点C作CD⊥BA交BA的延长线于点D,连接AC.
(1)求∠OAC的值;
(2)求证:CD是⊙O的切线.
四、解答题(二)(3个题,每题8分,共24分)
21.(8分)某历史文化街区需要加装一批垃圾分类提示牌和垃箱.根据需求,提示牌比垃圾箱多5个,且提示牌和垃圾箱的个数之和不少于100个,则至少购买垃圾箱多少个?
22.(8分)如图,在直角三角形ABC中,∠C=90°,AC=40,BC=30,作△ABC的内接矩形CDEF.设DE=x,求x取何值时矩形的面积最大?
23.(8分)如图,点A在反比例函数y=(其中k>0)图象上,OA=2,以点A为圆心,OA长为半径画弧交x轴正半轴于点B.
(1)当OB=4时,求k的值;
(2)过点B作BC⊥OB交反比例函数的图象于点C,连接OC交AB于点D,求的值.
五、解答题(三)(2个题,每题10分,共20分)
24.(10分)已知抛物线C1:y=﹣x2﹣x+4交x轴于点A、B,顶点为M,A、B、M关于原点的对称点分别是E、F、N.
(1)求点A、B的坐标;
(2)求出经过E、且以N为顶点的抛物线C2的表达式;
(3)抛物线C2与y轴交点为D,点P是抛物线C2在第四象限部分上一动点,点Q是y轴上一动点,求出一组P、Q的值,使得以点D、P、Q为顶点的三角形与△EFD相似.
25.(10分)在△ABC中,AC=BC=10,AB=12,点D是AB边上的一点.
(1)如图1,过点D作DM⊥AC于点M,DN⊥BC于点N,求DM+DN的值;
(2)将∠B沿着过点D的直线折叠,使点B落在AC边的点P处(不与点A、C重合),折痕交BC边于点E;
①如图2,当点D是AB的中点时,求AP的长度;
②如图3,设AD=a,若存在两次不同的折痕,使点B落在AC边上两个不同的位置,求a的取值范围.
2021年广东省佛山市顺德区中考数学一模试卷
参考答案与试题解析
一、选择题(10个题,每题3分,共30分)
1.(3分)2020年,我国脱贫攻坚战取得了全面胜利,现行标准下的9899万农村贫困人口全部脱贫,其中9899万用科学记数法表示为( )
A.989.9×105 B.98.99×106 C.9.899×107 D.0.9899×108
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数;当原数的绝对值<1时,n是负整数.
【解答】解:9899万=98990000=9.899×107,
故选:C.
2.(3分)如图所示的几何体是由几个大小相同的小正方体搭成的,其俯视图是( )
A. B.
C. D.
【分析】根据俯视图是从上面看到的图形,从上面看有两层,上层有4个正方形,下层有一个正方形且位于左二的位置.
【解答】解:从上面看,得到的视图是:,
故选:A.
3.(3分)下列运算正确的是( )
A.a5÷a2=a3 B.3a2+a=3a3
C.(a2)3=a5 D.a(a+1)=a2+1
【分析】各式利用同底数幂的除法,合并同类项法则,幂的乘方运算法则,以及单项式乘以多项式法则判断即可.
【解答】解:A、原式=a3,此选项计算正确;
B、原式不能合并,此选项计算错误;
C、原式=a6,此选项计算错误;
D、原式=a2+a,此选项计算错误.
故选:A.
4.(3分)为了估计某地区梅花鹿的数量,先捕捉20只梅花鹿做上标记,然后放走,待有标记的梅花鹿完全混合于鹿群后,第二次捕捉100只梅花鹿,发现其中5只有标记.估计这个地区的梅花鹿的数量约有( )只.
A.200 B.300 C.400 D.500
【分析】设这个地区的梅花鹿的数量约有x只,根据做标记的梅花鹿熟练所占比例等于捕捉100只梅花鹿中有标记的只数所占比例列出方程,解之即可.
【解答】解:设这个地区的梅花鹿的数量约有x只,
根据题意,得:=,
解得x=400,
经检验:x=400是分式方程的解,
所以这个地区的梅花鹿的数量约400只,
故选:C.
5.(3分)已知a=+1介于两个连续自然数之间,则下列结论正确的是( )
A.1<a<2 B.2<a<3 C.3<a<4 D.4<a<5
【分析】估算确定出的大小范围,进而确定出所求即可.
【解答】解:∵9<13<16,
∴3<<4,即4<+1<5,
则4<a<5.
故选:D.
6.(3分)如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE,若∠CAE=65°,∠E=70°,且AD⊥BC,则∠BAC的度数为( )
A.60° B.85° C.75° D.90°
【分析】先根据旋转的性质得∠C=∠E=70°,∠BAC=∠DAE,再根据垂直的定义得∠AFC=90°,则利用互余计算出∠CAF=90°﹣∠C=20°,所以∠DAE=∠CAF+∠EAC=85°,于是得到∠BAC=85°.
【解答】解:∵△ABC绕点A逆时针旋转得到△ADE,
∴∠C=∠E=70°,∠BAC=∠DAE,
∵AD⊥BC,
∴∠AFC=90°,
∴∠CAF=90°﹣∠C=90°﹣70°=20°,
∴∠DAE=∠CAF+∠EAC=20°+65°=85°,
∴∠BAC=∠DAE=85°.
故选:B.
7.(3分)如图,E是平行四边形ABCD边AD延长线上一点,且DE=AD,连接BE、CE、BD.若AB=BE,则四边形BCED是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
【分析】由平行四边形的性质得到AD∥BC,AD=BC,AB=DC,继而证得四边形BCED是平行四边形,再证得BE=DC,根据矩形的判定即可证得▱BCED是矩形.
【解答】解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,AB=DC,
∴DE∥BC,
∵DE=AD,
∴DE=BC,
∴四边形BCED是平行四边形,
∵AB=BE,
∴BE=DC,
∴▱BCED是矩形,
故选:B.
8.(3分)如图,一次函数y=x+1的图象与反比例函数y=的图象的一个交点为A(2,m),则不等式>3的解集是( )
A.x>2 B.0<x<2
C.x>0 D.x<﹣3或0<x<2
【分析】由点A在一次函数图象上利用一次函数图象上点的坐标特征即可求出点A的坐标,根据图象即可求得.
【解答】解:∵点A在一次函数y=x+1的图象上,
∴m=2+1=3,
∴点A的坐标为(2,3).
由图象可知,不等式>3的解集是0<x<2,
故选:B.
9.(3分)如图,AB为⊙O的直径,C、D为⊙O上两点,∠BCD=30°,BD=2,则AB的长度为( )
A.3 B.4 C.5 D.6
【分析】构造直角三角形,利用直角三角形30度角的性质解决问题即可.
【解答】解:如图,连接AD.
∵AB是直径,
∴∠ADB=90°,
∵∠A=∠DCB=30°,BD=2,
∴AB=2BD=4,
故选:B.
10.(3分)若关于x的不等式组有且只有8个整数解,关于y的方程=1的解为非负数,则满足条件的整数a的值为( )
A.﹣8 B.﹣10
C.﹣8或﹣10 D.﹣8或﹣9或﹣10
【分析】解不等式组,得到不等式组的解集,根据整数解的个数判断a的取值范围,解分式方程,用含有a的式子表示y,根据解的非负性求出a的取值范围,确定符合条件的整数a,相加即可.
【解答】解:不等式组,
解①得x≤5,
解②得x>,
∴不等式组的解集为<x≤5;
∵不等式组有且只有8个整数解,
∴﹣3≤<﹣2,
解得﹣10≤a<﹣7;
解分式方程=1得y=﹣a﹣1(a≠8);
∵方程的解为非负数,
∴﹣a﹣1≥0即a≤﹣1;
综上可知:﹣10≤a<﹣7;
∵a是整数,
∴a=﹣8或﹣9或﹣10.
故选:D.
二、填空题(7个题,每题4分,共28分)
11.(4分)因式分解:x2﹣16= (x+4)(x﹣4) .
【分析】直接利用平方差公式分解因式得出答案.
【解答】解:x2﹣16=(x+4)(x﹣4).
故答案为:(x+4)(x﹣4).
12.(4分)若关于x的一元二次方程x2﹣2x+c=0没有实数根.则实数c取值范围是 c>1 .
【分析】利用判别式的意义得到△=(﹣2)2﹣4c<0,然后解不等式即可.
【解答】解:根据题意得△=(﹣2)2﹣4c<0,
解得c>1.
故答案为c>1.
13.(4分)一个正多边形的每个内角都是144°,则这个多边形的内角和为 1440° .
【分析】首先根据内角的度数可得外角的度数,再根据外角和为360°可得边数,利用内角和公式可得答案.
【解答】解:∵一个正多边形的每个内角都是144°,
∴它的每一个外角都是:180°﹣144°=36°,
∴它的边数为:360°÷36=10,
∴这个多边形的内角和为:180°(10﹣2)=1440°,
故答案为:1440°.
14.(4分)在边长为2的正方形ABCD中,点E是AB的中点,EF⊥BD于点F,则EF的长度 .
【分析】根据正方形的性质和等腰直角三角形的性质即可得到结论.
【解答】解:∵四边形ABCD是正方形,
∴∠ABD=45°,
∵AB=2,点E是AB的中点,
∴BE=AB=1,
∵EF⊥BD,
∴∠EFB=90°,
∴EF=BE=,
故答案为:.
15.(4分)某校组织了一次初三科技小制作比赛,有A、B、C、D四个班共提供了100件参赛作品.C班提供的参赛作品的获奖率为50%,其它几个班的参赛作品情况及获奖情况绘制在图1和图2两幅尚不完整的统计图中,则获奖率最高的班级是 C班 .
【分析】根据题意和统计图中的数据,可以计算各个班的获奖率,从而可以得到哪个班的获奖率最高.
【解答】解:由统计图可得,
A班的获奖率为:14÷(100×35%)×100%=40%,
B班的获奖率为:11÷[100×(1﹣35%﹣20%﹣20%)]×100%=44%,
C班的获奖率为50%,
D班的获奖率为:8÷(100×20%)×100%=40%,
由上可得,获奖率最高的班级是C班,
故答案为:C班.
16.(4分)如图,在A点有一个热气球,由于受西风的影响,以20米/分的速度沿与地面成75°角的方向飞行,10分钟后到达C处,此时热气球上的人测得地面上的B点俯角为30°,则A、B两点间的距离为 200 米.
【分析】作AD⊥BC于D,根据速度和时间先求得AC的长,在Rt△ACD中,求得∠ACD的度数,再求得AD的长度,然后根据∠B=30°求出AB的长.
【解答】解:如图,过点A作AD⊥BC,垂足为D,
在Rt△ACD中,∠ACD=75°﹣30°=45°,
AC=20×10=200(米),
∴AD=AC•sin45°=100(米).
在Rt△ABD中,
∵∠B=30°,
∴AB=2AD=200(米).
故答案为:200.
17.(4分)如图,在四边形ABCD中,AB=CB,AD=CD.若∠ABD=∠ACD=30°,AD=1,则△ABC的内切圆面积 (结果保留π).
【分析】根据AB=CB,AD=CD,得出BD为AC的垂直平分线;利用等腰三角形的三线合一可得∠ABC=60°,进而得出△ABC为等边三角形;利用∠ACD=30°,得出△BCD为直角三角形,解直角三角形,求得等边三角形ABC的边长,再利用内心的性质求出圆的半径,圆的面积可求.
【解答】解:如图,设AC与BD交于点F,△ABC的内心为O,连接OA.
∵AB=CB,AD=CD,
∴BD是线段AC的垂直平分线.
∴AC⊥BD,AF=FC.
∵AB=BC,BF⊥AC,
∴∠ABF=∠CBF=30°.
∴∠ABC=60°.
∴△ABC为等边三角形.
∴∠BAC=∠ACB=60°.
∵∠ACD=30°,
∴∠BCD=∠ACD+∠ACB=30°+60°=90°.
∵CD=AD=1,
∴BC=.
∴AB=BC=AC=.
∵AB=BC,BF⊥AC,
∴AF=AC=.
∵O为,△ABC的内心,
∴∠OAF=∠BAC=30°.
∴OF=AF•tan30°=.
∴△ABC的内切圆面积为π•=.
故答案为.
三、解答题(一)(3个题,每题6分,共18分)
18.(6分)计算:2cos30°﹣()﹣2++|1﹣|.
【分析】原式利用特殊角的三角函数值,负整数指数幂法则,立方根定义,以及绝对值的代数意义计算即可求出值.
【解答】解:原式=2×﹣4﹣2+﹣1
=﹣4﹣2+﹣1
=2﹣7.
19.(6分)先化简,再计算:(+)÷,其中x满足x2﹣2x+2=0.
【分析】根据分式的混合运算法则把原式化简,整体代入计算,得到答案.
【解答】解:原式=(﹣)×
=×
=,
∵x2﹣2x+2=0,
∴x2﹣2x=﹣2,
∴原式==﹣1.
20.(6分)如图,M是⊙O的半径OA的中点,弦BC⊥AO于点M,过点C作CD⊥BA交BA的延长线于点D,连接AC.
(1)求∠OAC的值;
(2)求证:CD是⊙O的切线.
【分析】(1)如图,连接OB,OC,构造菱形ABOC,利用菱形的性质和圆的性质推知△AOC是等边三角形,则∠OAC=60°;
(2)想证明CD是⊙O的切线,只需推知OC⊥CD即可.
【解答】(1)解:如图,连接OB,OC,
∵弦BC⊥AO于点M,AO是半径,
∴点M是BC的中点.
又∵点M是AO的中点,
∴四边形ABOC是菱形.
∴AC=OC.
又∵OA=OC,
∴AC=OC=OA.
∴△AOC是等边三角形,
∴∠OAC=60°;
(2)证明:由(1)知,四边形ABOC是菱形,△AOC是等边三角形.
∴∠ABO=∠ACO=60°.
∴∠ABC=∠ABO=30°,∠OCB=∠ACO=30°.
∵CD⊥BA,
∴∠D=90°.
∴∠BCD=60°.
∴∠OCD=∠OCB+∠BCD=90°,即OC⊥CD.
又∵OC是半径,
∴CD是⊙O的切线.
四、解答题(二)(3个题,每题8分,共24分)
21.(8分)某历史文化街区需要加装一批垃圾分类提示牌和垃箱.根据需求,提示牌比垃圾箱多5个,且提示牌和垃圾箱的个数之和不少于100个,则至少购买垃圾箱多少个?
【分析】设购买x个垃圾箱,则购买(x+5)个提示牌,根据提示牌和垃圾箱的个数之和不少于100个,即可得出关于x的一元一次不等式,解之取其中的最小整数值即可得出结论.
【解答】解:设购买x个垃圾箱,则购买(x+5)个提示牌,
依题意得:(x+5)+x≥100,
解得:x≥.
又∵x为整数,
∴x的最小值为48.
答:至少购买垃圾箱48个.
22.(8分)如图,在直角三角形ABC中,∠C=90°,AC=40,BC=30,作△ABC的内接矩形CDEF.设DE=x,求x取何值时矩形的面积最大?
【分析】设矩形CDEF为S,证明△ADE∽△ACB,利用相似比得到x:30=(40﹣CD):40,则用x表示出CD,再利用矩形的面积公式得到S=x•,然后利用二次函数的性质解决问题.
【解答】解:设矩形CDEF为S,
∵四边形CDEF为矩形,
∴DE∥BC,
∴△ADE∽△ACB,
∴DE:BC=AD:AC,即x:30=(40﹣CD):40,
∴CD=,
∴S=x•
=﹣(x﹣15)2+300,
当x=15时,S有最大值,最大值为300.
即x取15时矩形的面积最大.
23.(8分)如图,点A在反比例函数y=(其中k>0)图象上,OA=2,以点A为圆心,OA长为半径画弧交x轴正半轴于点B.
(1)当OB=4时,求k的值;
(2)过点B作BC⊥OB交反比例函数的图象于点C,连接OC交AB于点D,求的值.
【分析】(1)过A点作x轴垂线段,即可得到A点坐标,进而可求k值;
(2)利用图中相似三角形的性质可求比值.
【解答】解:(1)作AF⊥x轴于F,交OC于E.
∵OA=AB,由等腰三角形三线合一性质可得OF=BF=OB=2.
∴AF==4.
∴点A的坐标为(2,4).
故k=xy=2×4=8.
(2∵点A、C在反比例函数图象上,由反比例函数图象上点的性质可得OF•AF=OB•BC.
∵OF=.
∴AF=2BC.
由∠EFO=∠CBO=90°,
∠EOF=∠COB.
∴△OEF∽△OCB,
∴.
∴EF=.
AE=AF﹣EF=2BC﹣=.
又由AF∥CB,
∴∠AED=∠BCD,
∴△AED∽△BCD.
∴.
故.
五、解答题(三)(2个题,每题10分,共20分)
24.(10分)已知抛物线C1:y=﹣x2﹣x+4交x轴于点A、B,顶点为M,A、B、M关于原点的对称点分别是E、F、N.
(1)求点A、B的坐标;
(2)求出经过E、且以N为顶点的抛物线C2的表达式;
(3)抛物线C2与y轴交点为D,点P是抛物线C2在第四象限部分上一动点,点Q是y轴上一动点,求出一组P、Q的值,使得以点D、P、Q为顶点的三角形与△EFD相似.
【分析】(1)令y=0,由﹣x2﹣x+4=0求得的解就是点A、B的横坐标;
(2)由(1)得到点A、B、M关于原点的对称点的坐标,然后利用顶点式求得抛物线C2的表达式;
(3)先结合图形的特点,构造出与△EFD相似且顶点分别在y轴上和抛物线上的三解形,再利用相似三角形的性质求解.
【解答】解:(1)当y=0时,由﹣x2﹣x+4=0,得x1=﹣4,x2=3,
∴A(﹣4,0)、B(3,0).
(2)由y=﹣x2﹣x+4=﹣(x)2+,得抛物线C1的顶点M(,+),
∵点E、F、N分别与点A、B、M关于原点对称,
∴E(4,0)、F(﹣3,0)、N(,);
设经过点E且顶点为N的抛物线C2的解析式为y=a(x﹣)2,
则(4﹣)2a=0,解得a=,
∴抛物线C2的解析式为y=x2﹣x﹣4.
(3)如图,作DP⊥AD交抛物线C2于点P,作PR⊥y轴于点R,在点R上方的y轴上取一点Q,使RQ=RP,则∠PQD=∠QPR=45°;
由y=x2﹣x﹣4,得D(0,﹣4).
∴OD=OB=4,∠DEF=∠EDQ=45°,
又∵∠PDQ=90°﹣∠FDH=∠DFE,
∴△QDP∽△EFD.
作FH∥PD交y轴于点H,则∠DFH=90°;
∵∠HFO=90°﹣∠OAD=∠ADO,
∴=tan∠ADO=,
∴OH=×3=.
设直线FH的解析式为y=kx+,则﹣3k+=0,解得k=,
∴y=x+,
∴直线DP的解析式为y=x﹣4;
由,得,(不符合题意,舍去).
∴P(,);
∵QR=PR=,
∴点Q的纵坐标为+=,
∴Q(0,).
综上所述,P(,),Q(0,).
25.(10分)在△ABC中,AC=BC=10,AB=12,点D是AB边上的一点.
(1)如图1,过点D作DM⊥AC于点M,DN⊥BC于点N,求DM+DN的值;
(2)将∠B沿着过点D的直线折叠,使点B落在AC边的点P处(不与点A、C重合),折痕交BC边于点E;
①如图2,当点D是AB的中点时,求AP的长度;
②如图3,设AD=a,若存在两次不同的折痕,使点B落在AC边上两个不同的位置,求a的取值范围.
【分析】(1)如图1中,连接CD,过点B作BE⊥AC于E,过点C作CH⊥AB于H.利用勾股定理求出CH,再利用面积法求出DM+DN的值.
(2)①如图2中,连接PB,CD.证明PB⊥AC,CD⊥AB,利用面积法求出PB,可得结论.
②如图3中,过点C作CH⊥AB于H,过点D作DP⊥AC于P.求出DP=DB时AD的值,结合图形即可判断.
【解答】解:(1)如图1中,连接CD,过点B作BE⊥AC于E,过点C作CH⊥AB于H.
∵CA=CB,CH⊥AB,
∴AH=HB=6,
∵S△ABC=S△ACD+S△BCD,DM⊥AC,DN⊥BC,
∴•AB•CH=•AC•DM+•BC•DN,
∴×12×8=×10×DM+×10×DN,
∴DM+DN=.
(2)①如图2中,连接PB,CD.
∵CA=CB,AD=DB,
∴CD⊥AB,
由(1)可知,CD=8,
∵DP=DA=DB,
∴∠APB=90°,即BP⊥AC,
∵•AB•CD=•AC•BP,
∴BP=,
∴AP===.
②如图3中,过点C作CH⊥AB于H,过点D作DP⊥AC于P.
∵CA=CB,CH⊥AB,
∴AH=HB=6,
∴CH===8,
当DB=DP时,设BD=PD=x,则AD=12﹣x,
∵sinA==,
∴=,
∴x=,
∴AD=AB﹣BD=,
观察图形可知当6<a<时,存在两次不同的折叠,使点B落在AC边上两个不同的位置.
2023年广东省佛山市顺德区红旗中学中考数学一模试卷(含解析): 这是一份2023年广东省佛山市顺德区红旗中学中考数学一模试卷(含解析),共15页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2023年广东省佛山市顺德区拔萃实验学校初中中考数学一模试卷: 这是一份2023年广东省佛山市顺德区拔萃实验学校初中中考数学一模试卷,共15页。
2023年广东省佛山市顺德区拔萃实验学校中考数学一模试卷(含解析): 这是一份2023年广东省佛山市顺德区拔萃实验学校中考数学一模试卷(含解析),共26页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。












