2021年河北省承德市中考数学一模试卷

这是一份2021年河北省承德市中考数学一模试卷，共27页。试卷主要包含了选择题，四象限，则k的取值范围是，解答题等内容，欢迎下载使用。

2021年河北省承德市中考数学一模试卷
一、选择题（本大题共16个小题，1-10题，每题3分，11-16题，每题2分，共42分.在每小题给出的四个选项中，只有一项是符合题目要求的）
1．（3分）下列方程中，一元二次方程是（　　）
A．x2+ B．ax2+bx
C．（x﹣1）（x+2）＝1 D．3x2﹣2xy﹣5y2＝0
2．（3分）一元二次方程4x2﹣4x+1＝0根的情况是（　　）
A．有两个相等的实数根 B．有两个不相等的实数根
C．没有实数根 D．无法确定
3．（3分）已知甲、乙两地相距s（km），汽车从甲地匀速行驶到乙地，则汽车行驶的时间t（h）与行驶速度v（km/h）的函数关系图象大致是（　　）
A． B．
C． D．
4．（3分）下列各点中，在函数y＝﹣图象上的是（　　）
A．（﹣2，﹣4） B．（2，3） C．（﹣1，6） D．（﹣，3）
5．（3分）若双曲线位于第二、四象限，则k的取值范围是（　　）
A．k＜1 B．k≥1 C．k＞1 D．k≠1
6．（3分）抛物线y＝（x+5）2﹣1的顶点坐标是（　　）
A．（5，﹣1） B．（﹣5，1） C．（5，1） D．（﹣5，﹣1）
7．（3分）在平面直角坐标系中，将抛物线y＝3x2先向右平移1个单位，再向上平移2个单位，得到的抛物线的解析式是（　　）
A．y＝3（x+1）2+2 B．y＝3（x+1）2﹣2
C．y＝3（x﹣1）2+2 D．y＝3（x﹣1）2﹣2
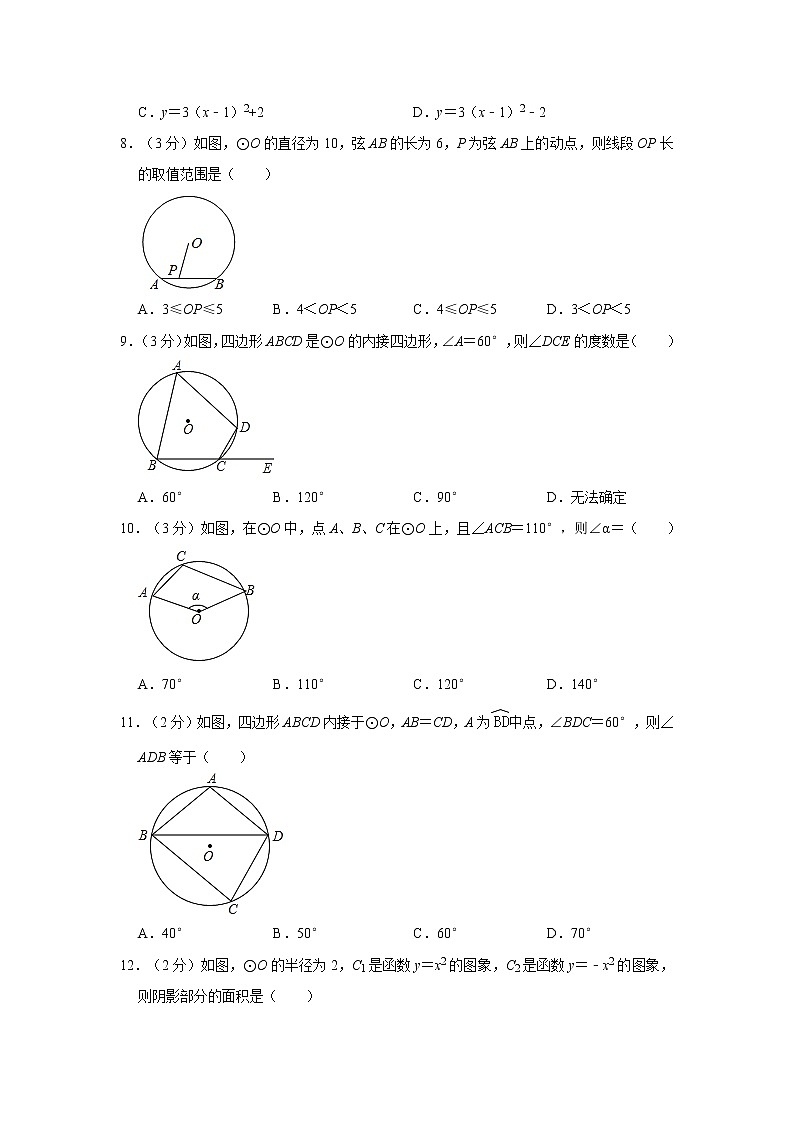
8．（3分）如图，⊙O的直径为10，弦AB的长为6，P为弦AB上的动点，则线段OP长的取值范围是（　　）

A．3≤OP≤5 B．4＜OP＜5 C．4≤OP≤5 D．3＜OP＜5
9．（3分）如图，四边形ABCD是⊙O的内接四边形，∠A＝60°，则∠DCE的度数是（　　）

A．60° B．120° C．90° D．无法确定
10．（3分）如图，在⊙O中，点A、B、C在⊙O上，且∠ACB＝110°，则∠α＝（　　）

A．70° B．110° C．120° D．140°
11．（2分）如图，四边形ABCD内接于⊙O，AB＝CD，A为中点，∠BDC＝60°，则∠ADB等于（　　）

A．40° B．50° C．60° D．70°
12．（2分）如图，⊙O的半径为2，C1是函数y＝x2的图象，C2是函数y＝﹣x2的图象，则阴影部分的面积是（　　）

A．π B．2π C．4π D．都不对
13．（2分）反比例函数y＝（m≠0）的图象如图所示，以下结论：①常数m＜﹣1；②在每个象限内，y随x的增大而增大；③若A（﹣1，h），B（2，k）在图象上，则h＜k；④若P（x，y）在图象上，则P′（﹣x，﹣y）也在图象上，其中正确的是（　　）

A．①② B．②③ C．③④ D．①④
14．（2分）如图，已知双曲线y＝（k＜0）经过直角三角形OAB斜边OA的中点D，且与直角边AB相交于点C．若点A的坐标为（﹣6，4），则△AOC的面积为（　　）

A．12 B．9 C．6 D．4
15．（2分）如图是二次函数y＝ax2+bx+c的部分图象，y＜0时自变量x的取值范围是（　　）

A．﹣1＜x＜5 B．x＞5 C．x＜﹣1且x＞5 D．x＜﹣1或x＞5
16．（2分）关于二次函数y＝x2﹣6x+a+27，下列说法错误的是（　　）
A．若将图象向上平移10个单位，再向左平移2个单位后过点（4，5），则a＝﹣5
B．当x＝12时，y有最小值a﹣9
C．x＝2对应的函数值比最小值大7
D．当a＜0时，图象与x轴有两个不同的交点
二、填空题（本大题共4个小题：17、18每小题3分，19、20每空2分，共14分把正确答案填在横线上）
17．（3分）已知x＝1是关于x的方程x2+mx+n＝0的一个根，则m+n的值是　 　．
18．（3分）抛物线y＝x2+bx+c经过点A（0，3），B（2，3），抛物线的对称轴为　 　．
19．（4分）如图，在平面直角坐标系xOy中，已知A（8，0），C（0，6），矩形OABC的对角线交于点P，点M在经过点P的函数y＝的图象上运动，k的值为　 　，OM长的最小值为　 　．

20．（4分）如图已知A1，A2，A3，…An是x轴上的点，且OA1＝A1A2＝A2A3＝A3A4＝…＝An﹣1An＝1，分别过点A1，A2，A3，…An作x轴的垂线交二次函数y＝x2（x＞0）的图象于点P1，P2，P3，…Pn，若记△OA1P1的面积为S1，过点P1作P1B1⊥A2P2于点B1，记△P1B1P2的面积为S2，过点P2作P2B2⊥A3P3于点B2，记△P2B2P3的面积为S3，…依次进行下去，则S3＝　 　，最后记△Pn﹣1Bn﹣1Pn（n＞1）的面积为Sn，则Sn＝　 　．

三、解答题（本大题共8小题，共64分。解答应写出文字说明、证明过程或演算步骤。）
21．（8分）解方程：
（1）x2﹣2x﹣15＝0；
（2）4x（2x+1）＝3（2x+1）．
22．（6分）如图所示，点A（，3）在双曲线y＝上，点B在双曲线y＝上，且AB∥x轴，C，D在x轴上，若四边形ABCD为矩形，求它的面积．

23．（8分）已知二次函数的解析式是y＝．
（1）用配方法将y＝化成y＝a（x﹣h）2+k的形式，并写出该二次函数的对称轴和顶点坐标；
（2）二次函数y＝的图象与x轴相交吗？说明理由；若相交，求出交点坐标．
24．（8分）某学习小组在学习了函数及函数图象的知识后，想利用此知识来探究周长一定时，矩形的面积与边长函数关系式的图象．请将他们的探究过程补充完整．
（1）列函数表达式：若矩形的周长为8，设矩形的一边长为x，面积为y，则有y＝　 　；
（2）上述函数表达式中，自变量x的取值范围是　 　；
（3）列表：
x
…
0.5
1
1.5
2
2.5
3
3.5
…
y
…
1.75
3
3.75
4
3.75
3
m
…
写出m＝　 　；
（4）画图：在平面直角坐标系中已描出了上表中部分各对应值为坐标的点，请你画出该函数的图象．

25．（8分）如图，A、B两点的坐标分别为（﹣2，0），（0，3），将线段AB绕点B逆时针旋转90°得到线段BC，过点C作CD⊥OB，垂足为D，反比例函数y＝的图象经过点C．
（1）直接写出点C的坐标，并求反比例函数的解析式；
（2）点P在反比例函数y＝的图象上，当△PCD的面积为3时，求点P的坐标．

26．（8分）如图，△ABC中，AB＝AC，⊙O是△ABC的外接圆，BO的延长交边AC于点D．
（1）求证：∠BAC＝2∠ABD；
（2）当△BCD是等腰三角形时，求∠BCD的大小．

27．（8分）如图，在△ABC中，AC＝BC，D是AB上一点，⊙O经过点A、C、D，交BC于点E，过点D作DF∥BC，交⊙O于点F．
求证：（1）四边形DBCF是平行四边形；
（2）AF＝EF．

28．（10分）甲经销商库存有1200套A品牌服装，每套进价400元，每套售价500元，一年内可卖完．现市场上流行B品牌服装，每套进价300元，每套售价600元，但一年内只允许经销商一次性订购B品牌服装，一年内B品牌服装销售无积压．因甲经销商无流动资金，只有低价转让A品牌服装，用转让来的资金购进B品牌服装，并销售．经与乙经销商协商，甲、乙双方达成转让协议，转让价格y（元/套）与转让数量x（套）之间的函数关系式为y＝．若甲经销商转让x套A品牌服装，一年内所获总利润为w（元）．
（1）求转让后剩余的A品牌服装的销售款Q1（元）与x（套）之间的函数关系式；
（2）求B品牌服装的销售款Q2（元）与x（套）之间的函数关系式；
（3）求w（元）与x（套）之间的函数关系式，并求w的最大值．

2021年河北省承德市中考数学一模试卷
参考答案与试题解析
一、选择题（本大题共16个小题，1-10题，每题3分，11-16题，每题2分，共42分.在每小题给出的四个选项中，只有一项是符合题目要求的）
1．（3分）下列方程中，一元二次方程是（　　）
A．x2+ B．ax2+bx
C．（x﹣1）（x+2）＝1 D．3x2﹣2xy﹣5y2＝0
【分析】本题根据一元二次方程的定义解答．
一元二次方程必须满足四个条件：
（1）未知数的最高次数是2；
（2）二次项系数不为0；
（3）是整式方程；
（4）含有一个未知数．由这四个条件对四个选项进行验证，满足这四个条件者为正确答案．
【解答】解：
A、不是整式方程，故错误；方程二次项系数可能为0，故错误
B、不是方程；
C、符合一元二次方程的定义，正确；
D、方程含有两个未知数，故错误．
故选：C．
2．（3分）一元二次方程4x2﹣4x+1＝0根的情况是（　　）
A．有两个相等的实数根 B．有两个不相等的实数根
C．没有实数根 D．无法确定
【分析】根据根的判别式即可求出答案．
【解答】解：△＝16﹣4×1×4＝0，
故选：A．
3．（3分）已知甲、乙两地相距s（km），汽车从甲地匀速行驶到乙地，则汽车行驶的时间t（h）与行驶速度v（km/h）的函数关系图象大致是（　　）
A． B．
C． D．
【分析】根据实际意义，写出函数的解析式，根据函数的类型，以及自变量的取值范围即可进行判断．
【解答】解：根据题意有：v•t＝s；
故v与t之间的函数图象为反比例函数，
且根据实际意义v＞0、t＞0，
其图象在第一象限．
故选：C．
4．（3分）下列各点中，在函数y＝﹣图象上的是（　　）
A．（﹣2，﹣4） B．（2，3） C．（﹣1，6） D．（﹣，3）
【分析】根据反比例函数中k＝xy的特点对各选项进行分析即可．
【解答】解：A、∵（﹣2）×（﹣4）＝8≠﹣6，∴此点不在反比例函数的图象上，故本选项错误；
B、∵2×3＝6≠﹣6，∴此点不在反比例函数的图象上，故本选项错误；
C、∵（﹣1）×6＝﹣6，∴此点在反比例函数的图象上，故本选项正确；
D、∵（﹣）×3＝﹣≠﹣6，∴此点不在反比例函数的图象上，故本选项错误．
故选：C．
5．（3分）若双曲线位于第二、四象限，则k的取值范围是（　　）
A．k＜1 B．k≥1 C．k＞1 D．k≠1
【分析】由反比例函数图象的位置在第二、四象限，可以得出k﹣1＜0，然后解这个不等式就可以求出k的取值范围．
【解答】解：∵双曲线位于第二、四象限，
∴k﹣1＜0，
∴k＜1．
故选：A．
6．（3分）抛物线y＝（x+5）2﹣1的顶点坐标是（　　）
A．（5，﹣1） B．（﹣5，1） C．（5，1） D．（﹣5，﹣1）
【分析】根据二次函数的顶点求解即可．
【解答】解：抛物线y＝（x+5）2﹣1的顶点坐标是（﹣5，﹣1），
故选：D．
7．（3分）在平面直角坐标系中，将抛物线y＝3x2先向右平移1个单位，再向上平移2个单位，得到的抛物线的解析式是（　　）
A．y＝3（x+1）2+2 B．y＝3（x+1）2﹣2
C．y＝3（x﹣1）2+2 D．y＝3（x﹣1）2﹣2
【分析】先根据抛物线的顶点式得到抛物线y＝3x2的对称轴为直线x＝0，顶点坐标为（0，0），则抛物线y＝3x2向右平移1个单位，再向上平移2个单位得到的抛物线的对称轴为直线x＝1，顶点坐标为（1，2），然后再根据顶点式即可得到平移后抛物线的解析式．
【解答】解：∵抛物线y＝3x2的对称轴为直线x＝0，顶点坐标为（0，0），
∴抛物线y＝3x2向右平移1个单位，再向上平移2个单位得到的抛物线的对称轴为直线x＝1，顶点坐标为（1，2），
∴平移后抛物线的解析式为y＝3（x﹣1）2+2．
故选：C．
8．（3分）如图，⊙O的直径为10，弦AB的长为6，P为弦AB上的动点，则线段OP长的取值范围是（　　）

A．3≤OP≤5 B．4＜OP＜5 C．4≤OP≤5 D．3＜OP＜5
【分析】连接OA，过点O作OH⊥AB于H，根据垂径定理求出AH，根据勾股定理求出OH，根据垂线段最短解答即可．
【解答】解：连接OA，过点O作OH⊥AB于H，
则AH＝HB＝AB＝3，
由勾股定理得，OH＝＝4，
当点P与点A（或点B）重合时，OP最大，当点P与得H重合时，OP最小，
∴线段OP长的取值范围是4≤OP≤5，
故选：C．

9．（3分）如图，四边形ABCD是⊙O的内接四边形，∠A＝60°，则∠DCE的度数是（　　）

A．60° B．120° C．90° D．无法确定
【分析】直接利用圆内接四边形的性质：外角等于它的内对角得出答案．
【解答】解：∵四边形ABCD为⊙O的内接四边形，
∴∠DCE＝∠A＝60°，
故选：A．
10．（3分）如图，在⊙O中，点A、B、C在⊙O上，且∠ACB＝110°，则∠α＝（　　）

A．70° B．110° C．120° D．140°
【分析】作所对的圆周角∠ADB，如图，利用圆内接四边形的性质得∠ADB＝70°，然后根据圆周角定理求解．
【解答】解：作所对的圆周角∠ADB，如图，
∵∠ACB+∠ADB＝180°，
∴∠ADB＝180°﹣110°＝70°，
∴∠AOB＝2∠ADB＝140°．
故选：D．

11．（2分）如图，四边形ABCD内接于⊙O，AB＝CD，A为中点，∠BDC＝60°，则∠ADB等于（　　）

A．40° B．50° C．60° D．70°
【分析】连接OA、OB、OD，OC，求出＝＝，求出∠AOB＝∠AOD＝∠DOC，根据圆周角定理求出∠BOC，再求出∠AOB，最后根据圆周角定理求出即可．
【解答】解：连接OA、OB、OD，OC，
∵∠BDC＝60°，
∴∠BOC＝2∠BDC＝120°，
∵AB＝DC，
∴∠AOB＝∠DOC，
∵A为的中点，
∴＝，
∴∠AOB＝∠AOD，
∴∠AOB＝∠AOD＝∠DOC＝×（360°﹣∠BOC）＝80°，
∴∠ADB＝AOB＝40°，
故选：A．
12．（2分）如图，⊙O的半径为2，C1是函数y＝x2的图象，C2是函数y＝﹣x2的图象，则阴影部分的面积是（　　）

A．π B．2π C．4π D．都不对
【分析】不规则图形面积通过对称转化为可求的图形面积．
【解答】解：∵C1是函数y＝x2的图象，C2是函数y＝﹣x2的图象，
∴两函数图象关于x轴对称，
∴阴影部分面积即是半圆面积，
∴阴影部分的面积S＝＝2π．
故选：B．
13．（2分）反比例函数y＝（m≠0）的图象如图所示，以下结论：①常数m＜﹣1；②在每个象限内，y随x的增大而增大；③若A（﹣1，h），B（2，k）在图象上，则h＜k；④若P（x，y）在图象上，则P′（﹣x，﹣y）也在图象上，其中正确的是（　　）

A．①② B．②③ C．③④ D．①④
【分析】根据反比例函数的图象的位置确定其比例系数的符号，利用反比例函数的性质进行判断即可．
【解答】解：∵反比例函数的图象位于一三象限，
∴m＞0
故①错误；
当反比例函数的图象位于一三象限时，在每一象限内，y随x的增大而减小，故②错误；
将A（﹣1，h），B（2，k）代入y＝得到h＝﹣m，2k＝m，
∵m＞0
∴h＜k
故③正确；
将P（x，y）代入y＝得到m＝xy，
将P′（﹣x，﹣y）代入y＝得到m＝xy，
故P（x，y）在图象上，则P′（﹣x，﹣y）也在图象上
故④正确，
故选：C．
14．（2分）如图，已知双曲线y＝（k＜0）经过直角三角形OAB斜边OA的中点D，且与直角边AB相交于点C．若点A的坐标为（﹣6，4），则△AOC的面积为（　　）

A．12 B．9 C．6 D．4
【分析】△AOC的面积＝△AOB的面积﹣△BOC的面积，由点A的坐标为（﹣6，4），根据三角形的面积公式，可知△AOB的面积＝12，由反比例函数的比例系数k的几何意义，可知△BOC的面积＝|k|．只需根据OA的中点D的坐标，求出k值即可．
【解答】解：∵OA的中点是D，点A的坐标为（﹣6，4），
∴D（﹣3，2），
∵双曲线y＝经过点D，
∴k＝﹣3×2＝﹣6，
∴△BOC的面积＝|k|＝3．
又∵△AOB的面积＝×6×4＝12，
∴△AOC的面积＝△AOB的面积﹣△BOC的面积＝12﹣3＝9．
故选：B．
15．（2分）如图是二次函数y＝ax2+bx+c的部分图象，y＜0时自变量x的取值范围是（　　）

A．﹣1＜x＜5 B．x＞5 C．x＜﹣1且x＞5 D．x＜﹣1或x＞5
【分析】先求出抛物线与x轴的交点坐标，根据图象即可解决问题．
【解答】解：由图象可知，抛物线与x轴的交点坐标分别为（﹣1，0）和（5，0），
∴y＜0时，x的取值范围为x＜﹣1或x＞5．
故选：D．

16．（2分）关于二次函数y＝x2﹣6x+a+27，下列说法错误的是（　　）
A．若将图象向上平移10个单位，再向左平移2个单位后过点（4，5），则a＝﹣5
B．当x＝12时，y有最小值a﹣9
C．x＝2对应的函数值比最小值大7
D．当a＜0时，图象与x轴有两个不同的交点
【分析】求出二次函数平移之后的表达式，将（4，5）代入，求出a即可判断A；将函数表达式化为顶点式，即可判断B；求出当x＝2时的函数值，减去函数最小值即可判断C；写出函数对应方程的根的判别式，根据a值判断判别式的值，即可判断D．
【解答】解：A、将二次函数向上平移10个单位，再向左平移2个单位后，
表达式为：，
若过点（4，5），
则，解得：a＝﹣5，故选项正确；
B、∵，开口向上，
∴当x＝12 时，y有最小值a﹣9，故选项正确；
C、当x＝2时，y＝a+16，最小值为a﹣9，a+16﹣（a﹣9）＝25，即x＝2对应的函数值比最小值大25，故选项错误；
D、△＝，当a＜0时，9﹣a＞0，
即方程有两个不同的实数根，即二次函数图象与x轴有两个不同的交点，故选项正确，
故选：C．
二、填空题（本大题共4个小题：17、18每小题3分，19、20每空2分，共14分把正确答案填在横线上）
17．（3分）已知x＝1是关于x的方程x2+mx+n＝0的一个根，则m+n的值是　﹣1　．
【分析】根据一元二次方程的解的定义，将x＝1代入一元二次方程x2+mx+n＝0，即可求得m+n的值．
【解答】解：∵x＝1是一元二次方程x2+mx+n＝0的一个根，
∴x＝1满足一元二次方程x2+mx+n＝0，
∴1+m+n＝0，
∴m+n＝﹣1；
故答案为：﹣1．
18．（3分）抛物线y＝x2+bx+c经过点A（0，3），B（2，3），抛物线的对称轴为　直线x＝1　．
【分析】先根据抛物线上两点的纵坐标相等可知此两点关于对称轴对称，再根据中点坐标公式求出这两点横坐标的中点坐标即可．
【解答】解：∵抛物线y＝x2+bx+c经过点A（0，3）和B（2，3），
∴此两点关于抛物线的对称轴对称，
∴x＝＝1．
故答案为：直线x＝1．
19．（4分）如图，在平面直角坐标系xOy中，已知A（8，0），C（0，6），矩形OABC的对角线交于点P，点M在经过点P的函数y＝的图象上运动，k的值为　12　，OM长的最小值为　2　．

【分析】先根据P（4，3），求得k＝4×3＝12，进而得出y＝，再根据双曲线的对称性可得，当点M在第一象限角平分线上时，OM最短，即当x＝y时，x＝，解得x＝±2，进而得到OM的最小值．
【解答】解：∵A（8，0），C（0，6），矩形OABC的对角线交于点P，
∴P（4，3），
代入函数y＝可得，k＝4×3＝12，
∴y＝，
∵点M在经过点P的函数y＝的图象上运动，
∴根据双曲线的对称性可得，当点M在第一象限角平分线上时，OM最短，
当x＝y时，x＝，
解得x＝±2，
又∵x＞0，
∴x＝2，
∴M（2，2），
∴OM＝＝2，
故答案为：12，2．
20．（4分）如图已知A1，A2，A3，…An是x轴上的点，且OA1＝A1A2＝A2A3＝A3A4＝…＝An﹣1An＝1，分别过点A1，A2，A3，…An作x轴的垂线交二次函数y＝x2（x＞0）的图象于点P1，P2，P3，…Pn，若记△OA1P1的面积为S1，过点P1作P1B1⊥A2P2于点B1，记△P1B1P2的面积为S2，过点P2作P2B2⊥A3P3于点B2，记△P2B2P3的面积为S3，…依次进行下去，则S3＝　　，最后记△Pn﹣1Bn﹣1Pn（n＞1）的面积为Sn，则Sn＝　　．

【分析】先根据二次函数图象上点的坐标特征，求出P1（1，），则根据三角形面积公式计算出S1＝，同样可得S2＝；S3＝，S4＝，所有相应三角形的面积等于分母为4，分子为奇数的分式，从而得到Sn＝．
【解答】解：当x＝1时，y＝x2＝，则P1（1，），所以S1＝×1×＝；
当x＝2时，y＝x2＝2，则P2（2，2），所以S2＝×1×（2﹣）＝；
当x＝3时，y＝x2＝，则P3（3，），所以S3＝×1×（﹣2）＝，
同样方法可得S4＝，
所以Sn＝．
故答案为，．
三、解答题（本大题共8小题，共64分。解答应写出文字说明、证明过程或演算步骤。）
21．（8分）解方程：
（1）x2﹣2x﹣15＝0；
（2）4x（2x+1）＝3（2x+1）．
【分析】利用因式分解法求解即可．
【解答】解：（1）∵x2﹣2x﹣15＝0，
∴（x﹣5）（x+3）＝0，
则x﹣5＝0或x+3＝0，
解得x1＝5，x2＝﹣3；

（2）∵4x（2x+1）＝3（2x+1），
∴4x（2x+1）﹣3（2x+1）＝0，
则（2x+1）（4x﹣3）＝0，
∴2x+1＝0或4x﹣3＝0，
解得x1＝﹣0.5，x2＝0.75．
22．（6分）如图所示，点A（，3）在双曲线y＝上，点B在双曲线y＝上，且AB∥x轴，C，D在x轴上，若四边形ABCD为矩形，求它的面积．

【分析】由点A的坐标以及AB∥x轴，可得出点B的坐标，从而得出AD、AB的长度，利用矩形的面积公式即可得出结论．
【解答】解：∵A（，3），AB∥x轴，点B在双曲线y＝上，
∴B（1，3），
∴AB＝1﹣＝，AD＝3，
∴S＝AB•AD＝×3＝2．
23．（8分）已知二次函数的解析式是y＝．
（1）用配方法将y＝化成y＝a（x﹣h）2+k的形式，并写出该二次函数的对称轴和顶点坐标；
（2）二次函数y＝的图象与x轴相交吗？说明理由；若相交，求出交点坐标．
【分析】（1）y＝＝（x2﹣6x+9）﹣+＝（x﹣3）2﹣2，即可求解；
（2）由（1）知a＝0，顶点在第四象限，抛物线开口向上，故图象与x轴相交，令y＝＝0，解得：x＝5或1，即可求解．
【解答】解：（1）y＝＝（x2﹣6x+9）﹣+＝（x﹣3）2﹣2，
故对称轴为x＝3，顶点坐标为：（3，﹣2）；
（2）由（1）知a＝0，顶点在第四象限，抛物线开口向上，故图象与x轴相交，
令y＝＝0，解得：x＝5或1，
故交点坐标为：（5，0）、（1，0）．
24．（8分）某学习小组在学习了函数及函数图象的知识后，想利用此知识来探究周长一定时，矩形的面积与边长函数关系式的图象．请将他们的探究过程补充完整．
（1）列函数表达式：若矩形的周长为8，设矩形的一边长为x，面积为y，则有y＝　y＝﹣x2+4x　；
（2）上述函数表达式中，自变量x的取值范围是　0＜x＜4　；
（3）列表：
x
…
0.5
1
1.5
2
2.5
3
3.5
…
y
…
1.75
3
3.75
4
3.75
3
m
…
写出m＝　1.75　；
（4）画图：在平面直角坐标系中已描出了上表中部分各对应值为坐标的点，请你画出该函数的图象．

【分析】根据二次函数，利用二次函数的性质即可解决问题．
【解答】解：（1）由题意：y＝x（4﹣x）＝﹣x2+4x．
故答案为：y＝﹣x2+4x；
（2）上述函数表达式中，自变量x的取值范围是0＜x＜4．
故答案为：0＜x＜4．
（3）x＝3.5时，y＝1.75，
∴m＝1.75．
故答案为：1.75．
（4）函数图象如图所示：

25．（8分）如图，A、B两点的坐标分别为（﹣2，0），（0，3），将线段AB绕点B逆时针旋转90°得到线段BC，过点C作CD⊥OB，垂足为D，反比例函数y＝的图象经过点C．
（1）直接写出点C的坐标，并求反比例函数的解析式；
（2）点P在反比例函数y＝的图象上，当△PCD的面积为3时，求点P的坐标．

【分析】（1）根据旋转的性质和全等三角形的性质求得C点的坐标，即可求得结论；
（2）由解析式设出P点的坐标，根据三角形面积公式得出方程，解方程可求得P点坐标．
【解答】解：（1）∵将线段AB绕点B逆时针旋转90°得到线段BC，
∴AB＝BC，∠ABC＝90°，
∵CD⊥OB，
∴∠CDB＝∠AOB＝∠ABC＝90°，
∴∠ABO+∠CBD＝∠CBD+∠DCB＝90°，
∴∠ABO＝∠DCB，
∴△ABO≌△BCD（AAS），
∴CD＝OB＝3，BD＝OA＝2，
∴OD＝3﹣2＝1，
∴C点的坐标为（3，1），
∴k＝3×1＝3，
∴反比例函数的解析式为：；
（2）设P（，m），
∵CD⊥y轴，CD＝3，
由△PCD的面积为3得：CD•|m﹣1|＝3，
∴×3|m﹣1|＝3，
∴m﹣1＝±2，
∴m＝3或m＝﹣1，
当m＝3时，＝1，当m＝﹣1时，＝﹣3，
∴点P的坐标为（1，3）或（﹣3，﹣1）．

26．（8分）如图，△ABC中，AB＝AC，⊙O是△ABC的外接圆，BO的延长交边AC于点D．
（1）求证：∠BAC＝2∠ABD；
（2）当△BCD是等腰三角形时，求∠BCD的大小．

【分析】（1）连接OA并延长AO交BC于E，证明∠BAC＝2∠BAE和∠ABD＝∠BAE即可得结论，
（2）设∠ABD为x，用x表示出有关的角，再列方程即得答案．
【解答】解（1）连接OA并延长AO交BC于E，
∵AB＝AC，
∴弧AB＝弧AC，
∵AE过圆心O，
∴AE垂直平分BC（平分弧的直径垂直平分弧所对的弦），
∴AE平分∠BAC，
∴∠BAC＝2∠BAE，
∵OA＝OB，
∴∠ABD＝∠BAE，
∴∠BAC＝2∠ABD；

（2）设∠ABD＝x，
由（1）知∠BAC＝2∠ABD＝2x，
∴∠BDC＝3x，
△BCD是等腰三角形，
①若BD＝BC，
则∠C＝∠BDC＝3x，
∵AB＝AC，
∴∠ABC＝∠C＝3x，
在△ABC中，∠ABC+∠C+∠BAC＝180°，
∴3x+3x+2x＝180°，
解得x＝22.5°，
∴∠BCD＝3x＝67.5°，
②若BC＝CD，则∠BDC＝∠CBD＝3x，
∴∠ABC＝∠ACB＝4x，
在△ABC中，∠ABC+∠C+∠BAC＝180°，
∴4x+4x+2x＝180°，
∴x＝18°，
∴∠BCD＝4x＝72°，
综上所述，△BCD是等腰三角形，∠BCD为67.5°或72°．
27．（8分）如图，在△ABC中，AC＝BC，D是AB上一点，⊙O经过点A、C、D，交BC于点E，过点D作DF∥BC，交⊙O于点F．
求证：（1）四边形DBCF是平行四边形；
（2）AF＝EF．

【分析】（1）根据等腰三角形的性质得出∠BAC＝∠B，根据平行线的性质得出∠ADF＝∠B，求出∠ADF＝∠CFD，根据平行线的判定得出BD∥CF，根据平行四边形的判定得出即可；
（2）求出∠AEF＝∠B，根据圆内接四边形的性质得出∠ECF+∠EAF＝180°，根据平行线的性质得出∠ECF+∠B＝180°，求出∠AEF＝∠EAF，根据等腰三角形的判定得出即可．
【解答】证明：（1）∵AC＝BC，
∴∠BAC＝∠B，
∵DF∥BC，
∴∠ADF＝∠B，
∵∠BAC＝∠CFD，
∴∠ADF＝∠CFD，
∴BD∥CF，
∵DF∥BC，
∴四边形DBCF是平行四边形；


（2）连接AE，
∵∠ADF＝∠B，∠ADF＝∠AEF，
∴∠AEF＝∠B，
∵四边形AECF是⊙O的内接四边形，
∴∠ECF+∠EAF＝180°，
∵BD∥CF，
∴∠ECF+∠B＝180°，
∴∠EAF＝∠B，
∴∠AEF＝∠EAF，
∴AF＝EF．
28．（10分）甲经销商库存有1200套A品牌服装，每套进价400元，每套售价500元，一年内可卖完．现市场上流行B品牌服装，每套进价300元，每套售价600元，但一年内只允许经销商一次性订购B品牌服装，一年内B品牌服装销售无积压．因甲经销商无流动资金，只有低价转让A品牌服装，用转让来的资金购进B品牌服装，并销售．经与乙经销商协商，甲、乙双方达成转让协议，转让价格y（元/套）与转让数量x（套）之间的函数关系式为y＝．若甲经销商转让x套A品牌服装，一年内所获总利润为w（元）．
（1）求转让后剩余的A品牌服装的销售款Q1（元）与x（套）之间的函数关系式；
（2）求B品牌服装的销售款Q2（元）与x（套）之间的函数关系式；
（3）求w（元）与x（套）之间的函数关系式，并求w的最大值．
【分析】（1）直接根据销售款＝售价×套数即可得出结论；
（2）根据转让价格y（元/套）与转让数量x（套）之间的函数关系式为y＝﹣x+360（100≤x≤1200）得出总件数，再与售价相乘即可；
（3）把（1）（2）中的销售款相加再减去成本即可．
【解答】解：（1）∵甲经销商库存有1200套A品牌服装，每套售价500元，转让x套给乙，
∴Q1＝500×（1200﹣x）＝﹣500x+600000（100≤x≤1200）；

（2）∵转让价格y（元/套）与转让数量x（套）之间的函数关系式为y＝﹣x+360（100≤x≤1200），B品牌服装，每套进价300元，
∴转让后可购买B服装套，
∴Q2＝×600＝﹣x2+720x（100≤x≤1200）；

（3）∵由（1）、（2）知，Q1＝﹣500x+600000，Q2＝﹣x2+720x，
∴w＝Q1+Q2﹣400×1200
＝﹣500x+600000﹣x2+720x﹣480000
＝﹣（x﹣550）2+180500，
当x＝550时，w有最大值，最大值为180500元．