

全国统考版2021届高考数学二轮复习验收仿真模拟卷二理含解析
展开高考仿真模拟卷(二)
(时间:120分钟;满分:150分)
第Ⅰ卷
一、选择题:本题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设集合A={x|x2-x-2>0},B={x|0<log2x<2},则A∩B=( )
A.(2,4) B.(1,1)
C.(-1,4) D.(1,4)
2.i为虚数单位,复数z满足z(1+i)=i,则|z|=( )
A. B.
C.1 D.
3.已知向量a=(x,1),b=(1,y),c=(2,-4),且a⊥c,b∥c,则|a+b|=( )
A. B.
C.2 D.10
4.函数f(x)=的图象大致为( )
5.若sin=,α∈,则tan 2α=( )
A.- B.
C.- D.
6.我国古代有着辉煌的数学研究成果.《周牌算经》、《九章算术》、《海岛算经》、《孙子算经》、……《缉古算经》等10部专著,有着十分丰富多彩的内容,是了解我国古代数学的重要文献.这10部专著中有7部产生于魏晋南北朝时期.某中学拟从这10部专著中选择2部作为“数学文化”校本课程学习内容,则所选2部专著中至少有一部是魏晋南北朝时期专著的概率为( )
A. B.
C. D.
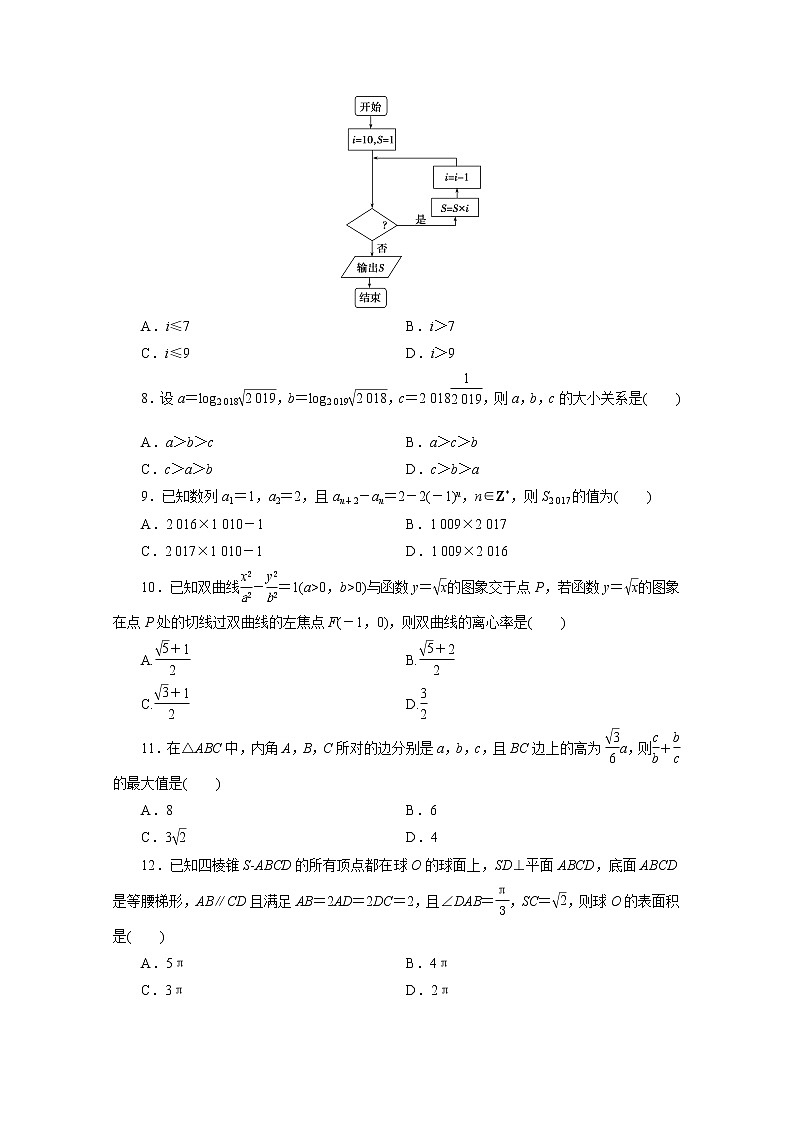
7.如图程序框图输出的结果是S=720,则判断框内应填的是( )
A.i≤7 B.i>7
C.i≤9 D.i>9
8.设a=log2 018,b=log2 019,c=2 018,则a,b,c的大小关系是( )
A.a>b>c B.a>c>b
C.c>a>b D.c>b>a
9.已知数列a1=1,a2=2,且an+2-an=2-2(-1)n,n∈Z*,则S2 017的值为( )
A.2 016×1 010-1 B.1 009×2 017
C.2 017×1 010-1 D.1 009×2 016
10.已知双曲线-=1(a>0,b>0)与函数y=的图象交于点P,若函数y=的图象在点P处的切线过双曲线的左焦点F(-1,0),则双曲线的离心率是( )
A. B.
C. D.
11.在△ABC中,内角A,B,C所对的边分别是a,b,c,且BC边上的高为a,则+的最大值是( )
A.8 B.6
C.3 D.4
12.已知四棱锥SABCD的所有顶点都在球O的球面上,SD⊥平面ABCD,底面ABCD是等腰梯形,AB∥CD且满足AB=2AD=2DC=2,且∠DAB=,SC=,则球O的表面积是( )
A.5π B.4π
C.3π D.2π
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
第Ⅱ卷
二、填空题:本题共4小题,每小题5分.
13.已知等差数列{an}的前n项和为Sn,a1=13,S3=S11,则Sn的最大值为________.
14.若在(a+3x)(1-)8关于x的展开式中,常数项为4,则x2的系数是________.
15.在平行四边形ABCD中,AC与BD交于点O,=,CE的延长线与AD交于点F,若=λ+ μ(λ,μ∈R),则λ+μ=________.
16.对于函数y=f(x),若存在区间[a,b],当x∈[a,b]时的值域为[ka,kb](k>0),则称y=f(x)为k倍值函数.若f(x)=ln x+x是k倍值函数,则实数k的取值范围是________.
三、解答题:解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分12分)已知函数f(x)=sin(3π+x)·cos(π-x)+cos2.
(1)求函数f(x)的单调递增区间;
(2)已知在△ABC中,A,B,C的对边分别为a,b,c,若f(A)=,a=2,b+c=4,求b,c.
18.(本小题满分12分)某次有1 000人参加的数学摸底考试,成绩的频率分布直方图如图所示,规定85分及其以上为优秀.
(1)下表是这次考试成绩的频数分布表,求正整数a,b的值;
成绩区间
[75,80)
[80,85)
[85,90)
[90,95)
[95,100)
人数
50
a
350
300
b
(2)现在要用分层抽样的方法从这1 000人的成绩中抽取40人的成绩进行分析,再从抽取的40名学生中,随机选取2名学生参加座谈会,记选取的2名学生中成绩为优秀的人数为X,求X的分布列与数学期望.
19.(本小题满分12分)如图,在几何体ABCDEF中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,FB=,M,N分别为EF,AB的中点.
(1)求证:MN∥平面FCB;
(2)若直线AF与平面FCB所成的角为30°,求平面MAB与平面FCB所成角的余弦值.
20.(本小题满分12分)已知椭圆C:+=1(a>b>0)的长轴长为4.
(1)若以原点为圆心,椭圆短半轴长为半径长的圆与直线y=x+2相切,求椭圆C的焦点坐标;
(2)若过原点的直线l与椭圆C相交于M,N两点,点P是椭圆C上使直线PM,PN的斜率存在的任意一点,记直线PM,PN的斜率分别为kPM,kPN,当kPM·kPN=-时,求椭圆C的方程.
21.(本小题满分12分)已知函数f(x)=ln x+(k∈R).
(1)若f(x)存在极小值h(k),且不等式h(k)≤ak对f(x)存在极小值的任意k恒成立,求实数a的取值范围;
(2)当k>0时,如果存在两个不相等的正数α,β使得f(α)=f(β),求证:α+β>2k.
请考生在22、23题中任选一题作答,如果多做,则按所做的第一题计分.
22.(本小题满分10分)选修44:坐标系与参数方程
在平面直角坐标系xOy中,曲线C1的参数方程为(α为参数),以O为极点,x轴的正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为ρ2=4ρsin θ-3.
(1)求曲线C1的普通方程与曲线C2的直角坐标方程;
(2)求曲线C1上的点与曲线C2上的点的距离的最小值.
23.(本小题满分10分)选修45:不等式选讲
已知函数f(x)=|x|+|x-1|.
(1)若f(x)≥|m-1|恒成立,求实数m的最大值M;
(2)在(1)成立的条件下,正实数a,b满足a2+b2=M,
证明:a+b≥2ab.
高考仿真模拟卷(二)
1.解析:选A.A={x|x<-1或x>2},B={x|1<x<4},所以A∩B=(2,4).故选A.
2.解析:选B.由z(1+i)=i得z=,
所以|z|===,故答案为B.
3.解析:选B.因为向量a=(x,1),b=(1,y),c=(2,-4),且a⊥c,b∥c,所以2x-4=0,2y=-4,解得x=2,y=-2,所以a=(2,1),b=(1,-2),所以a+b=(3,-1),所以|a+b|= =.
4.解析:选A.因为f(-x)===f(x),所以f(x)是偶函数,
可得图象关于y轴对称,排除C,D;当x>0时,f(x)=,f(1)=0,f<0,排除B.
5.解析:选A.因为sin=cos α=,
所以sin α=±,因为α∈,所以sin α=,所以tan α=,所以tan 2α===-,故选A.
6.解析:选A.设所选2部专著中至少有一部是魏晋南北朝时期专著为事件A,
所以P(A)==,因此P(A)=1-P(A)=1-=,故本题选A.
7.解析:选B.第一次运行,i=10,满足条件,S=1×10=10,i=9;
第二次运行,i=9满足条件,S=10×9=90,i=8;
第三次运行,i=8满足条件,S=90×8=720,i=7;
此时不满足条件,输出的S=720.
故条件应为8,9,10满足,i=7不满足,所以条件应为i>7.
8.解析:选C.因为1=log2 0182 018>a=log2 018>log2 018=,
b=log2 019<log2 019=,c=2 018>2 0180=1,故本题选C.
9.解析:选C.由递推公式可得:
当n为奇数时,an+2-an=4,数列{a2n-1}是首项为1,公差为4的等差数列,
当n为偶数时,an+2-an=0,数列{an}是首项为2,公差为0的等差数列,
S2 017=(a1+a3+…+a2 017)+(a2+a4+…+a2 016)
=1 009+×1 009×1 008×4+1 008×2
=2 017×1 010-1.本题选择C选项.
10.解析:选A.设P(x0,),所以切线的斜率为,
又因为在点P处的切线过双曲线的左焦点F(-1,0),
所以=,解得x0=1,所以P(1,1),因此2c=2,2a=-1,故双曲线的离心率是,故选A.
11.解析:选D.+=,这个形式很容易联想到余弦定理cos A=,①
而条件中的“高”容易联想到面积,a×a=bcsin A,即a2=2bcsin A,②
将②代入①得:b2+c2=2bc(cos A+sin A),
所以+=2(cos A+sin A)=4sin,当A=时取得最大值4,故选D.
12.解析:选A.依题意得,AB=2AD=2,∠DAB=,由余弦定理可得BD=,则AD2+DB2=AB2,
则∠ADB=,又四边形ABCD是等腰梯形,故四边形ABCD的外接圆直径为AB,设AB的中点为O1,球的半径为R,因为SD⊥平面ABCD,
所以R2=12+=,则S=4πR2=5π,故选A.
13.解析:因为S3=S11,可得3a1+3d=11a1+55d,把a1=13代入得d=-2.故Sn=13n-n(n-1)=-n2+14n,根据二次函数性质,当n=7时,Sn最大且最大值为49.
答案:49
14.解析:由题意得(1-)8展开式的通项为Tr+1=C(-)r=(-1)rCx,r=0,1,2,…,8,
所以(a+3x)(1-)8展开式的常数项为(-1)0C·a=a=4,所以(4+3x)(1-)8展开式中x2项的系数为4·(-1)6Cx+3x·(-1)3Cx=-56x2,
所以展开式中x2的系数是-56.故答案为-56.
答案:-56
15.解析:法一:因为=,==,所以==,所以=,由DF∥BC,得=,所以=+=+=++(+)=+=-+,所以λ=-,μ=,λ+μ=-.
法二:不妨设ABCD为矩形,建立平面直角坐标系如图,设AB=a,BC=b,则A(0,0),B(a,0),C(a,b),D(0,b),O,设E(x,y),因为=,所以(x,y-b)=,所以x=,y=b,即E,设F(0,m),因为∥,=(-a,m-b),=,所以ab+a(m-b)=0,解得m=b,即F,=.又=(a,b),=(-a,b),由=λ+μ,得=λ(a,b)+μ(-a,b)=((λ-μ)a,(λ+μ)b),所以λ+μ=-.
答案:-
16.解析:由题意得ln x+x=kx有两个不同的解,k=+1,则k′==0⇒x=e,因此当0
答案:
17.解:(1)因为f(x)=sin(3π+x)·cos(π-x)+cos2,
所以f(x)=(-sin x)·(-cos x)+(-sin x)2=sin 2x+=sin+.
由2kπ-≤2x-≤2kπ+,k∈Z,
得kπ-≤x≤kπ+,k∈Z,
即函数f(x)的单调递增区间是,k∈Z.
(2)由f(A)=得,sin+=,所以sin=1,
因为0<A<π,
所以0<2A<2π,-<2A-<,
所以2A-=,所以A=,
因为a=2,b+c=4,①
根据余弦定理得,
4=b2+c2-2bccos A=b2+c2-bc=(b+c)2-3bc=16-3bc,
所以bc=4,②
联立①②得,b=c=2.
18.解:(1)依题意得,a=0.04×5×1 000=200,b=0.02×5×1 000=100.
(2)设抽取的40名学生中,成绩为优秀的学生人数为x,则=,解得x=30,
即抽取的40名学生中,成绩为优秀的学生人数为30.
依题意,X的可能取值为0,1,2,
P(X=0)==,P(X=1)==,P(X=2)==,
所以X的分布列为
X
0
1
2
P
所以X的数学期望E(X)=0×+1×+2×=.
19.解:(1)证明:取BC的中点Q,连接NQ,FQ,则NQ=AC,NQ∥AC.
又MF=AC,MF∥AC,所以MF=NQ,MF∥NQ,则四边形MNQF为平行四边形,即MN∥FQ.
因为FQ⊂平面FCB,MN⊄平面FCB,
所以MN∥平面FCB.
(2)由AB∥CD,AD=DC=CB=1,∠ABC=60°可得∠ACB=90°,AC=,BC=1,AB=2.因为四边形ACFE为矩形,所以AC⊥平面FCB,则∠AFC为直线AF与平面FCB所成的角,即∠AFC=30°,所以FC=3.
因为FB=,所以FC⊥BC,则可建立如图所示的空间直角坐标系Cxyz,
所以A(,0,0),B(0,1,0),M,=,=.
设m=(x,y,z)为平面MAB的法向量,
则即
取x=2,则m=(2,6,1)为平面MAB的一个法向量.
又n=(,0,0)为平面FCB的一个法向量,
所以cos〈m,n〉===.
则平面MAB与平面FCB所成角的余弦值为.
20.解:(1)由题意知,b等于原点到直线y=x+2的距离,即b==,又2a=4,所以a=2,c2=a2-b2=2,所以椭圆C的两个焦点的坐标分别为,.
(2)由题意可设M(x0,y0),N(-x0,-y0),P(x,y),
则+=1,+=1,
两式相减得=-,
又kPM=,kPN=,
所以kPM·kPN=·==-,所以-=-,又a=2,所以b=1,故椭圆C的方程为+y2=1.
21.解:(1)f′(x)=-=,x>0.
当k≤0时,f′(x)>0,f(x)在(0,+∞)上单调递增,无极值.
当k>0时,当0<x<k时,f′(x)<0,当x>k时,f′(x)>0,故f(x)的单调递减区间是(0,k),单调递增区间是(k,+∞),f(x)的极小值为h(k)=f(k)=ln k+1.
当k>0时,h(k)≤ak恒成立,即ln k+1≤ak,即a≥恒成立.
令φ(k)=,则φ′(k)==,令φ′(k)=0,得k=1,当0<k<1时,φ′(k)>0,φ(k)单调递增,当k>1时,φ′(k)<0,φ(k)单调递减,故k=1为φ(k)在(0,+∞)上唯一的极大值点,也是最大值点,所以φ(k)max=φ(1)=1,所以a≥1,即实数a的取值范围是[1,+∞).
(2)证明:由(1)知,当k>0时,f(x)在(0,k)上单调递减,在(k,+∞)上单调递增,设α<β,则一定有0<α<k<β.
构造函数g(x)=f(x)-f(2k-x)=ln x+-ln (2k-x)-,0<x<k,
g′(x)=+--
=-
=.
因为0<x<k,所以g′(x)<0,即g(x)在(0,k)上单调递减,又f(k)-f(2k-k)=0,所以g(x)>0,所以f(x)>f(2k-x).
因为0<α<k,所以f(α)>f(2k-α),
因为f(α)=f(β),所以f(β)>f(2k-α),因为0<α<k,所以2k-α>k,又函数f(x)在(k,+∞)上单调递增,所以β>2k-α,所以α+β>2k.
22.解:(1)x2==(sin α+cos α)2=sin 2α+1=y,所以C1的普通方程为y=x2.将ρ2=x2+y2,ρsin θ=y代入C2的方程得x2+y2=4y-3,所以C2的直角坐标方程为x2+y2-4y+3=0.
(2)将x2+y2-4y+3=0变形为x2+(y-2)2=1,它的圆心为C(0,2).
设P(x0,y0)为C1上任意一点,则y0=x,从而|PC|2=(x0-0)2+(y0-2)2=x+(x-2)2=x-3x+4=+,所以当x=时,|PC|min=,
故曲线C1上的点与曲线C2上的点的距离的最小值为-1.
23.解:(1)由已知可得f(x)=
所以f(x)min=1,
所以只需|m-1|≤1,解得-1≤m-1≤1,
所以0≤m≤2,所以实数m的最大值M=2.
(2)证明:因为a2+b2≥2ab,
所以ab≤1,
所以≤1,当且仅当a=b时取等号,①
又≤,所以≤,
所以≤,当且仅当a=b时取等号,②
由①②得,≤,所以a+b≥2ab.
全国统考版2021届高考数学二轮复习验收仿真模拟卷五理含解析: 这是一份全国统考版2021届高考数学二轮复习验收仿真模拟卷五理含解析,共13页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
全国统考版2021届高考数学二轮复习验收仿真模拟卷十二理含解析: 这是一份全国统考版2021届高考数学二轮复习验收仿真模拟卷十二理含解析,共15页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
全国统考版2021届高考数学二轮复习验收仿真模拟卷七理含解析: 这是一份全国统考版2021届高考数学二轮复习验收仿真模拟卷七理含解析,共13页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












