人教版八年级下册17.1 勾股定理备课课件ppt

这是一份人教版八年级下册17.1 勾股定理备课课件ppt，共21页。PPT课件主要包含了教学目标，走进数学殿堂，∵S大正方形＝c2，a2c2－b2，b2c2-a2，公式变形，课堂小结等内容，欢迎下载使用。

能用勾股定理解决一些简单问题.
了解勾股定理的发现过程，掌握勾股定理的内容，会用面积法证明勾股定理.
通过利用勾股定理解决简单问题，体会数形结合的思想.
在中国古代，人们把弯曲成直角的手臂的上半部分称为“勾”，下半部分称为“股”.我国古代学者把直角三角形较短的直角边称为“勾”，较长的直角边称为“股”，斜边称为“弦”.
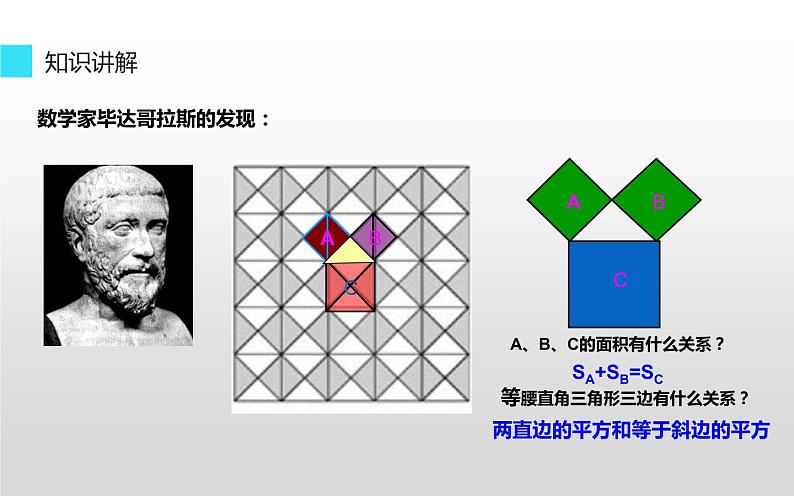
数学家毕达哥拉斯的发现：
A、B、C的面积有什么关系？
等腰直角三角形三边有什么关系？
两直边的平方和等于斜边的平方
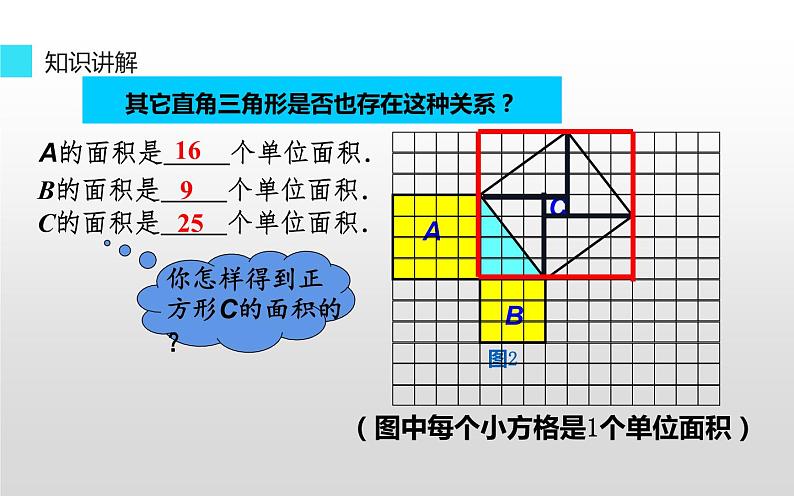
A的面积是 个单位面积．
B的面积是 个单位面积．
C的面积是 个单位面积．
（图中每个小方格是1个单位面积）
其它直角三角形是否也存在这种关系？
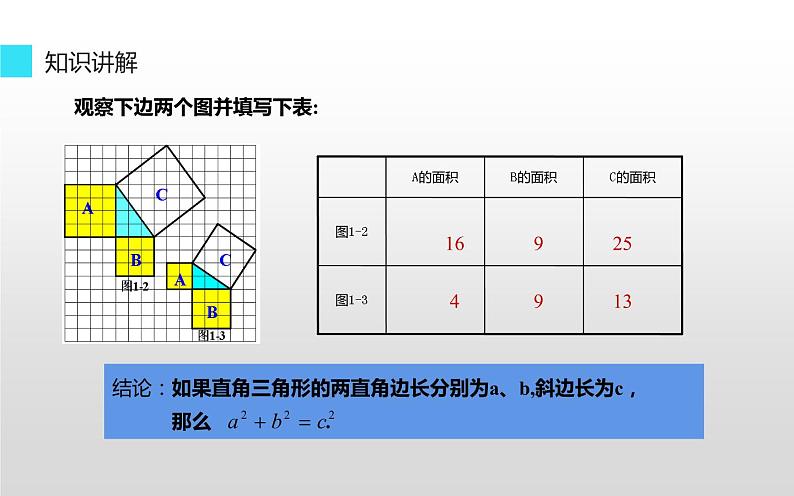
命题1：如果直角三角形的两直角边长分别为a，b,斜边长为c，那么a2+b2=c2.即：两直角边的平方和等于斜边的平方。
以直角三角形的两条直角边a、b为边作两个正方形，把两个正方形如图1连在一起，通过剪、拼把它拼成图2的样子.你能做到吗？试试看.
小活动：仿照课本中赵爽的思路，只剪两刀，将两个连体正方形，拼成一个新的正方形.
S小正方形＝(b-a)2,
∴S大正方形＝4·S三角形＋S小正方形，
毕达哥拉斯证法：请用四个全等的直角三角形按图示进行拼图，然后分析其面积关系后证明吧.
∴a2+b2+2ab=c2+2ab，
∴a2 +b2 =c2.
证明：∵S大正方形=(a+b)2=a2+b2+2ab,
∴a2 + b2 = c2.
美国第二十任总统伽菲尔德的“总统证法”.
如图，图中的三个三角形都是直角三角形，求证：a2 + b2 = c2.
如果直角三角形两直角边分别为a、b,斜边为c，那么
即直角三角形两直角边的平方和等于斜边的平方.
表示为：Rt△ABC中，∠C=90°
　　勾股定理给出了直角三角形三边之间的关系，即两直角边的平方和等于斜边的平方.
a2 + b2 =c2
1、 如图，在Rt△ABC中， ∠C=90°.
（1）若a=b=5,求c;
（2）若a=1,c=2,求b.
(2)在Rt△ABC中， ∠C=90° a=1,c=2 根据勾股定理得
利用勾股定理求直角三角形的边长
2、在Rt△ABC中，AB＝4，AC＝3，求BC的长.
解：本题斜边不确定，需分类讨论：当AB为斜边时，如图，当BC为斜边时，如图，
提示：当直角三角形中所给的两条边没有指明是斜边或直角边时，其中一较长边可能是直角边，也可能是斜边，这种情况下一定要进行分类讨论。
在Rt△ABC中， ∠C=90°,a,b为直角边，c为斜边，则有a2+b2=c2.
已知两边没有指明是直角边还是斜边时一定要分类讨论