

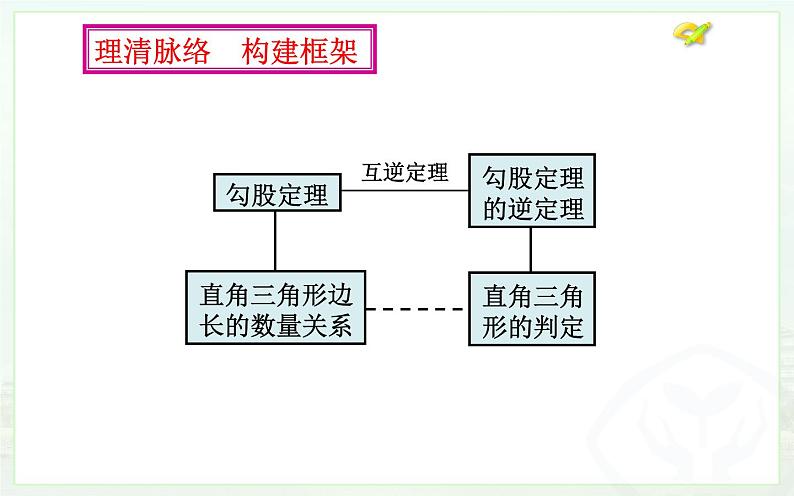




初中数学17.1 勾股定理教学ppt课件
展开1、掌握勾股定理和逆定理,理解原命题、逆命题、逆定理的概念及关系
2、熟练掌握勾股定理及逆定理的应用
课前认真阅读37页小结的内容,注意: 1、本章的知识结构图中体现了那些知识点之间的关系
2、在“回顾与思考”中提到的一个数学方法是什么?
3、带着“回顾与思考”中的5个问题快速浏览课本22页至34页的内容
知识点一:勾股定理 直角三角形两直角边a、b的平方和等于斜边c的平方。(即:a2+b2=c2) 要点诠释:勾股定理反映了直角三角形三边之间的关系,是直角三角形的重要性质之一,其主要应用:(1)已知直角三角形的两边求第三边(2)已知直角三角形的一边与另两边的比例关系,求直角三角形的另两边(3)利用勾股定理可以证明线段平方关系的问题
1.如图,已知在△ABC 中,∠B =90°,一直角边为a,斜边为b,则另一直角边c满足c2 = .
(一)知两边或一边一角型
勾股定理的直接应用
答案:因为∠B 所对的边是斜边.
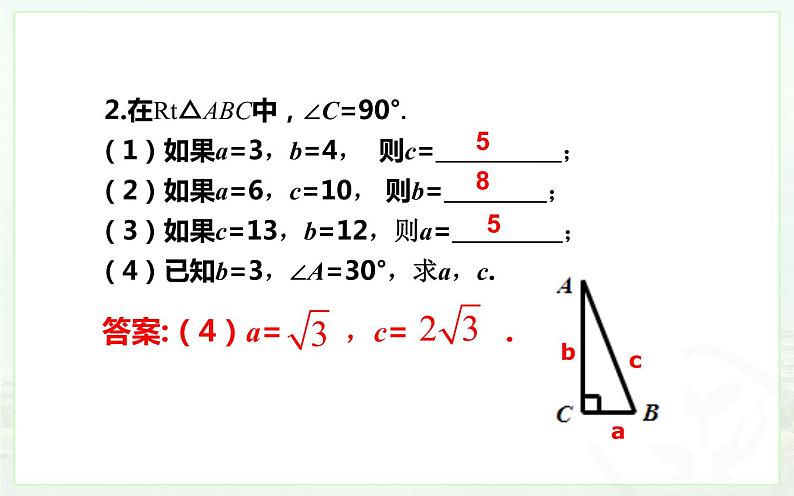
2.在Rt△ABC中,∠C=90°.(1)如果a=3,b=4, 则c= ; (2)如果a=6,c=10, 则b= ;(3)如果c=13,b=12,则a= ; (4)已知b=3,∠A=30°,求a,c.
答案:(4)a= ,c= .
1.如图,已知在△ABC 中,∠B =90°,若BC=4 , AB=x ,AC=8-x,则AB= ,AC= .2.在Rt△ABC 中,∠B=90°,b=34,a:c=8:15,则a= , c= .
(二)知一边及另两边关系型 (方程思想)
1. 对三角形边的分类. 已知一个直角三角形的两条边长是3 cm和4 cm,求第三条边的长.注意:这里并没有指明已知的两条边就是直角边,所以4 cm可以是直角边,也可以是斜边,即应分情况讨论.
答案:5 cm或 cm.
已知:在△ABC中,AB=15 cm,AC=13 cm,高AD=12 cm,求S△ABC.答案:第1种情况:如图1,在Rt△ADB和Rt△ADC中,分别由勾股定理,得BD=9,CD=5,所以BC=BD+ CD=9+5=14.故S△ABC=84(cm2).第2种情况,如图2,可得:S△ABC=24( cm2 ).
2. 对三角形高的分类. Zx```xk
1. 在一块平地上,张大爷家屋前9米远处有一棵大树.在一次强风中,这棵大树从离地面6米处折断倒下,量得倒下部分的长是10米.出门在外的张大爷担心自己的房子被倒下的大树砸到.大树倒下时能砸到张大爷的房子吗?( )A.一定不会B.可能会C.一定会D.以上答案都不对
用勾股定理解决简单的实际问题
2:如图,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,沿表面爬行的最短路程( 取3)是( ) A.20cm B.10cm C.14cm D.无法确定
3、已知:如图,△ABC的周长是24,∠C=90°,且 b=6,则三角形的面积是多少?
∵周长是24,且b=6
∴a+c=24-6=18
设a=x,则c=18-x
∴x2+62=(18-x)2
【点评】利用勾股定理解题决实际问题时,基本步骤是什么?Zx```xk1.把实际问题转化成数学问题,找出相应的直角三角形.2.在直角三角形中找出直角边,斜边.3.根据已知和所求,利用勾股定理建立方程解决问题
利用勾股定理表示无理数的方法:
(1)利用勾股定理把一个无理数表示成直角边是两个正整数的直角三角形的斜边.
(2)以原点为圆心,以无理数斜边长为半径画弧与数轴存在交点,在原点左边的点表示是负无理数,在原点右边的点表示是正无理数.
知识点二:利用勾股定理尺规作图
一用、勾股定理,定直角边大小
知识点三:勾股定理的逆定理 如果三角形的三边长:a、b、c,则有关系a2+b2=c2,那么这个三角形是直角三角形。 要点诠释:用勾股定理的逆定理判定一个三角形是否是直角三角形应注意: (1)首先确定最大边,不妨设最长边长为:c;(2)验证c2与a2+b2是否具有相等关系,若c2=a2+b2,则△ABC是以∠C为直角的直角三角形(若c2>a2+b2,则△ABC是以∠C为钝角的钝角三角形;若c2
1.下列各组线段中,能构成直角三角形的是( )A.2,3,4 B.3,4,6 C.5,12,13 D.4,6,7
2.已知a、b、c是△ABC三边的长,且满足关系式 ,则△ABC的形状是 ________________.
3. 如图,△ABC中,AB=AC,D是AC边上的一点,CD=1,BC= 5 ,BD=2.(1)求证:△BCD是直角三角形;(2)求△ABC的面积.
(1)证明:∵CD=1,BC= 5 ,BD=2,∴CD2+BD2=25 BC2=25,∴CD2+BD2=BC2∴△BDC是直角三角形;(2)解:设腰长AB=AC=x,在Rt△ADB中,∵AB2=AD2+BD2,∴x2=(x-1)2+22,解得
会用勾股定理及逆定理解决综合的问题
知识点四:1、勾股定理与勾股定理逆定理的区别与联系 区别:勾股定理是直角三角形的性质定理,而其逆定理是判定定理;联系:勾股定理与其逆定理的题设和结论正好相反,都与直角三角形有关。 2、互逆命题的概念 如果一个命题的题设和结论分别是另一个命题的结论和题设,这样的两个命题叫做互逆命题。如果把其中一个叫做原命题,那么另一个叫做它的逆命题。
写出下列命题的逆命题,并判断其真假.
2、等腰三角形是等边三角形.
3、如果一个整数的个位数字是5 ,那么这个整数能被5整除.
逆命题:两直线平行,同旁内角互补.真命题
逆命题:等边三角形是等腰三角形.真命题
逆命题:如果一个整数能被5整除,那么这个整数的个位数字是5.假命题
1、同旁内角互补,两直线平行.
你在本节课的收获是什么?还有什么困惑?
老师根据自己学生的实际情况布置
(作业备用题)1、教材67页探究2:如图,一架长为10m的梯子AB斜靠在墙上,梯子的顶端距地面的垂直距离为8m.问题:如果梯子的顶端下滑1m,那么它的底端是否也滑动1 m?
变式一:当梯子的顶端下滑多少米时,梯子顶端下滑的距离AC会等于梯子底端下滑的距离BD?
变式二:如果设梯子的长度为c米,AO=b米,BO=a米,请用含a、b的式子表示当梯子顶端下滑多少米时,梯子顶端下滑的距离AC会等于梯子底端下滑的距离BD?
2021学年第十七章 勾股定理17.1 勾股定理教学ppt课件: 这是一份2021学年第十七章 勾股定理17.1 勾股定理教学ppt课件,共30页。PPT课件主要包含了学习目标等内容,欢迎下载使用。
初中数学人教版八年级下册17.1 勾股定理教学ppt课件: 这是一份初中数学人教版八年级下册17.1 勾股定理教学ppt课件,共25页。PPT课件主要包含了情景引入,一直角边2,另一直角边2,斜边2,赵爽弦图,b-a,勾2+股2弦2,bc为正数,即勾2+股2弦2,知识要点等内容,欢迎下载使用。
初中数学17.1 勾股定理教学ppt课件: 这是一份初中数学17.1 勾股定理教学ppt课件,共22页。PPT课件主要包含了情境引入,SA+SBSC,探究新知,a2+b2c2,得出猜想,证明猜想,证明一赵爽弦图,勾股定理,SA225,SB25等内容,欢迎下载使用。













