2021年河北省中考数学模拟试题二

2021年河北省中考数学模拟试题二

一、选择题(本大题有16个小题,共42分.1~10小题各3分,11~16小题各2分.在每小题给出的四个选项中,只有一项是符合题目要求的)

1.下列计算不正确的是 (  )　　　　　　　　　　　　　

A.(-3)+(-4) =-7

B.(-3)×(-4)=12

C.(-3)-(-4)=1

D.(-3)÷(-4) =-

2.将矩形纸带按如图所示方式折叠成“V”字形,已知∠1=35°,则∠2的度数为 (  )

A.35° B.55° C.65° D.30°

3.下列整式中不是多项式4a3-a的因式的是 (  )

A.4a+1　　　 B.2a+1 C.2a-1　　 D.4a2-1

4.已知□tan 60°,在□内填入下列运算符号,运算结果是无理数的是 (  )

A.÷　　　 B.×　　  C.-　　　 D.+

5.已知某商品的进价是a元,销售旺季,商家将价格提高70%标价出售,销售旺季过后,商店又以标价的5折开展促销活动,促销时每件商品              (  )

A.亏损0.15a元 B.盈利0.35a元

C.盈利0.5a元 D.盈利0.85a元

6.如图所示,已知△ABC,则下列四个三角形中,与△ABC相似的是(  )

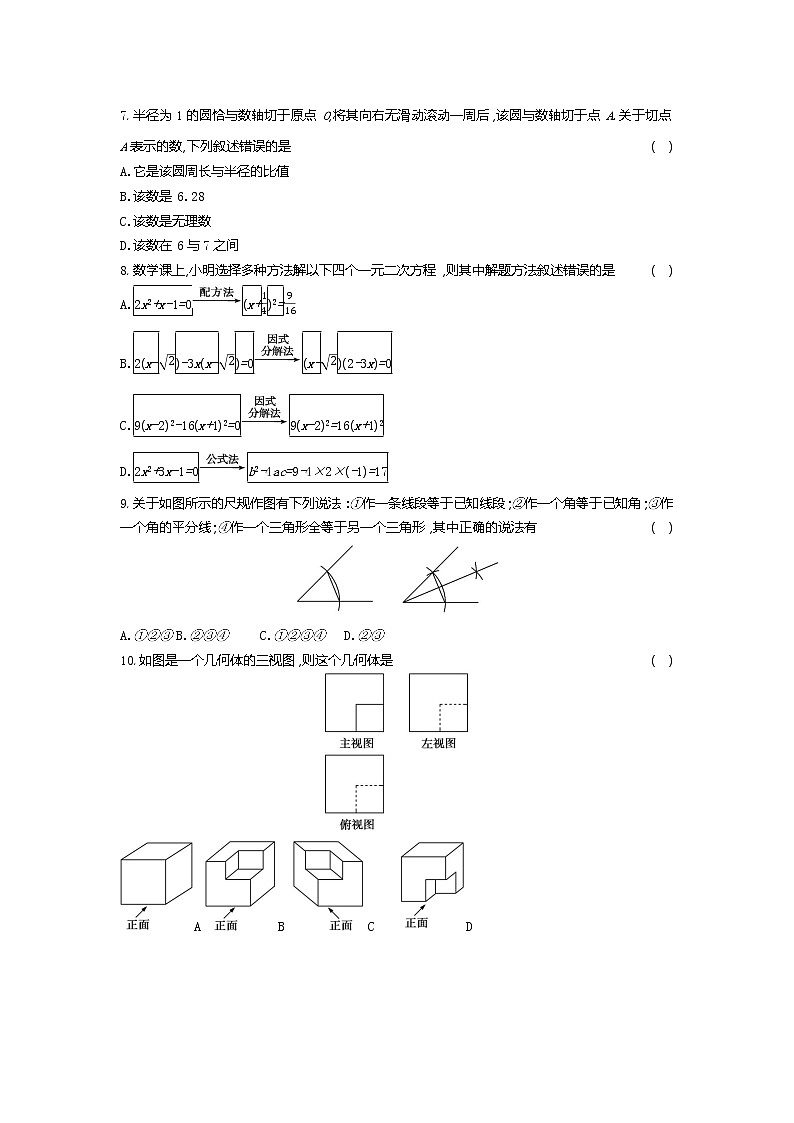
7.半径为1的圆恰与数轴切于原点O,将其向右无滑动滚动一周后,该圆与数轴切于点A.关于切点A表示的数,下列叙述错误的是              (  )

A.它是该圆周长与半径的比值

B.该数是6.28

C.该数是无理数

D.该数在6与7之间

8.数学课上,小明选择多种方法解以下四个一元二次方程,则其中解题方法叙述错误的是 (  )

A.2x2+x-1=0(x+)2=

B.2(x-)-3x(x-)=0(x-)(2-3x)=0

C.9(x-2)2-16(x+1)2=09(x-2)2=16(x+1)2

D.2x2+3x-1=0b2-4ac=9-4×2×(-1)=17

9.关于如图所示的尺规作图有下列说法:①作一条线段等于已知线段;②作一个角等于已知角;③作一个角的平分线;④作一个三角形全等于另一个三角形,其中正确的说法有              (  )

A.①②③ B.②③④  C.①②③④ D.②③

10.如图是一个几何体的三视图,则这个几何体是 (  )

A B C D

11.某校九年级(1)班要对某小组5名女生一分钟仰卧起坐的次数进行统计分析,发现数据36,42,56,5■,48中第四个数的个位数字被涂污看不清楚了,则下列统计量中与被涂污数字无关的是              (  )

A.平均数 B.方差

C.中位数 D.众数

12.已知函数y=(a+1)x2+ax-1,则下列说法正确的是 (  )

A.当a+1=0时,该函数的图象与x轴没有交点

B.当a=0时,该函数的图象与坐标轴有2个交点

C.当a≠-1时,该函数的图象与x轴总有2个交点

D.该函数的图象恒过点(-1,0)

13.如图,在Rt△ABC中,∠C=90°,∠BAC=30°,BC=1,延长CA到点D,使AD=AB,连接BD,利用此图解释的三角函数值中错误的是              (  )

A.tan 30°= B.tan 60°=

C.tan 15°=1+　　 D.tan 75°=2+

14.如图,两种边长不同的正方形按如图所示的方式无缝隙地拼在一起,若阴影图形P经过旋转可得到阴影图形Q,则旋转中心是              (  )

A.点A B.点B

C.点C D.点D

15.在平面直角坐标系中,已知点A(1,2),AB∥y轴,AB=2,若直线l:y=ax+1与线段AB有交点,则a的取值范围是              (  )

A.1≤a≤3 B.-1≤a≤1

C.-1≤a≤3 D.1≤a≤3或-1≤a≤1

16.如图,在菱形ABCD中,AB=8,∠B=60°,P是AB上一点,BP=5,Q是CD边上一动点,将四边形APQD沿直线PQ折叠,点A的对应点是点A'.当CA'的长度最小时,CQ的长为              (  )

A.7 B.6 C.5 D.6.5

二、填空题(本大题有3个小题,共12分.17~18小题各3分;19小题有3个空,每空2分)

17.式子有意义,则x的取值范围为　. 

18.由六个边长相等且形状完全相同的菱形组成如图所示的网格,菱形的顶点称为格点,O,A,B,C都在格点上,∠AOB=60°,则sin∠ABC= 　. 

19.如图,☉O的直径AB的长为10,点C为直径AB上方半圆上一动点(不与点A,B重合),连接AC,BC,CD平分∠ACB交☉O于点D,AE平分∠CAB交CD于点E,连接BE,AD,BD.

(1)AC·BC的最大值为　　; 

(2)AC+BC的最大值为　　; 

(3)△ABE的外接圆的半径为　　. 

20.(本小题满分8分)

已知“▲”和“■”分别表示0,1,2,3,4,5,6,7,8,9中的一个数字,例如:“■▲”表示个位数是“▲”、十位数是“■”的两位数;“3■”表示个位数是“■”、十位数是“3”的两位数.

(1)当“▲=■”时,若7■-▲2=14,求“▲”和“■”表示的数字;

(2)当“▲≠■”时,若多项式“■x2-▲”可以利用平方差公式在有理数范围内因式分解,且两位数“▲■”是完全平方数,求“▲”和“■”表示的数字.

21.(本小题满分8分)

问题探究:

已知ab=1,求证:+=1.

(1)淇淇是这样证明的:+===1.她的同桌嘉嘉发现,若将中的1代换成ab,则问题也可迎刃而解,请你帮嘉嘉完成证明过程.

方法应用:

(2)已知ab=1,请你根据嘉嘉的思路求+的值.

22.(本小题满分9分)

如图,直线l1:y=3x-1与y轴交于点A,直线l2经过点B(-1,4),与直线l1相交于点P(1,b),并分别与x轴、y轴相交于点C,E.

(1)求b的值及直线l2的函数解析式;

(2)连接AB,求△PAB的面积;

(3)当反比例函数y=的图象与线段BC有公共点时,请直接写出k的最大值和最小值.

23.(本小题满分9分)

如图,在等边三角形ABC中,AC=6,点O在AC上,且AO=2,点P从点B出发,沿BA运动至点A停止,连接OP,以点O为圆心、OP为半径作圆.

(1)当☉O经过点A,且点A,P不重合时,求BP的长;

(2)当☉O经过BC上的点D,且∠DOP=60°时,求证:BC与☉O相切于点D;

(3)已知点I是△AOP的内心,连接OI,AI,在点P从☉O与BC相切运动到☉O第一次经过点A的过程中,求∠AIO度数的取值范围.

　　　　　　　　　备用图(1) 　　　备用图(2)

24.(本小题满分10分)

六一期间,某儿童玩具经销商开展“买玩具返现金”促销活动,活动规定购买一件某款玩具返还现金x(元).根据往年活动经验可知,六一期间该玩具的日销售量y(件)与返还现金x之间的函数关系为y=x+40,返还现金后,销售每件该款玩具的利润z(元)与x之间的函数关系为z=-x+30.

(1)若销售一件该款玩具返还顾客30元,则六一期间销售这款玩具的总利润为多少元?

(2)在确保销售该款玩具不亏本的情况下,求日销售量y的最大值,以及此时购买每件该款玩具返还顾客的金额.

(3)当返还的金额为多少时,经销商可获得最大日销售利润,最大日销售利润是多少?

25.(本小题满分10分)

如图,在▱ABCD中,AB=8,AD=8,BD⊥AB.点P为射线CD上一动点,连接BP,以BP为直径作☉O,交边AD(不含端点)于点Q,连接PQ,BQ.

(1)填空:当点P与点D重合时,BQ=　　; 

(2)当的长度为时,求CP的长度;

(3)连接CQ,当圆心O恰好落在线段CQ上时,请直接写出CP的长度.

备用图

26.(本小题满分12分)

已知抛物线L1:y=ax2-4ax,其顶点为P.

(1)试说明无论a为何值,抛物线L1恒过两个点,并求出这两个点的坐标.

(2)抛物线L2:y=x2-x+c与y轴交于点B,顶点记为Q,记抛物线L1与x轴正半轴的交点为A.

①当a<0,x的取值范围为  　时,抛物线L1与L2均是y随x的增大而增大; 

②当BQ∥AP时,求a的值;

③若a=-1,H,G是抛物线L1上的两点,且点H,G的横坐标分别是-1,3,那么当抛物线L2与抛物线L1上点H,G之间的曲线(包含端点H,G)只有一个公共点时,请直接写出c的取值范围.

答案

一、选择题(本大题有16个小题,共42分.1~10小题各3分,11~16小题各2分.在每小题给出的四个选项中,只有一项是符合题目要求的)

1.下列计算不正确的是 ( D )

A.(-3)+(-4) =-7

B.(-3)×(-4)=12

C.(-3)-(-4)=1

D.(-3)÷(-4) =-

2.将矩形纸带按如图所示方式折叠成“V”字形,已知∠1=35°,则∠2的度数为 ( A )

A.35° B.55° C.65° D.30°

3.下列整式中不是多项式4a3-a的因式的是 ( A )

A.4a+1　　　 B.2a+1 C.2a-1　　 D.4a2-1

4.已知□tan 60°,在□内填入下列运算符号,运算结果是无理数的是 ( D )

A.÷　　　 B.×　　  C.-　　　 D.+

5.已知某商品的进价是a元,销售旺季,商家将价格提高70%标价出售,销售旺季过后,商店又以标价的5折开展促销活动,促销时每件商品              ( A )

A.亏损0.15a元 B.盈利0.35a元

C.盈利0.5a元 D.盈利0.85a元

6.如图所示,已知△ABC,则下列四个三角形中,与△ABC相似的是( C )

7.半径为1的圆恰与数轴切于原点O,将其向右无滑动滚动一周后,该圆与数轴切于点A.关于切点A表示的数,下列叙述错误的是              ( B )

A.它是该圆周长与半径的比值

B.该数是6.28

C.该数是无理数

D.该数在6与7之间

8.数学课上,小明选择多种方法解以下四个一元二次方程,则其中解题方法叙述错误的是 ( C )

A.2x2+x-1=0(x+)2=

B.2(x-)-3x(x-)=0(x-)(2-3x)=0

C.9(x-2)2-16(x+1)2=09(x-2)2=16(x+1)2

D.2x2+3x-1=0b2-4ac=9-4×2×(-1)=17

9.关于如图所示的尺规作图有下列说法:①作一条线段等于已知线段;②作一个角等于已知角;③作一个角的平分线;④作一个三角形全等于另一个三角形,其中正确的说法有              ( C )

A.①②③ B.②③④  C.①②③④ D.②③

10.如图是一个几何体的三视图,则这个几何体是 ( D )

A B C D

11.某校九年级(1)班要对某小组5名女生一分钟仰卧起坐的次数进行统计分析,发现数据36,42,56,5■,48中第四个数的个位数字被涂污看不清楚了,则下列统计量中与被涂污数字无关的是              ( C )

A.平均数 B.方差

C.中位数 D.众数

12.已知函数y=(a+1)x2+ax-1,则下列说法正确的是 ( D )

A.当a+1=0时,该函数的图象与x轴没有交点

B.当a=0时,该函数的图象与坐标轴有2个交点

C.当a≠-1时,该函数的图象与x轴总有2个交点

D.该函数的图象恒过点(-1,0)

13.如图,在Rt△ABC中,∠C=90°,∠BAC=30°,BC=1,延长CA到点D,使AD=AB,连接BD,利用此图解释的三角函数值中错误的是              ( C )

A.tan 30°= B.tan 60°=

C.tan 15°=1+　　 D.tan 75°=2+

14.如图,两种边长不同的正方形按如图所示的方式无缝隙地拼在一起,若阴影图形P经过旋转可得到阴影图形Q,则旋转中心是              ( C )

A.点A B.点B

C.点C D.点D

15.在平面直角坐标系中,已知点A(1,2),AB∥y轴,AB=2,若直线l:y=ax+1与线段AB有交点,则a的取值范围是              ( D )

A.1≤a≤3 B.-1≤a≤1

C.-1≤a≤3 D.1≤a≤3或-1≤a≤1

16.如图,在菱形ABCD中,AB=8,∠B=60°,P是AB上一点,BP=5,Q是CD边上一动点,将四边形APQD沿直线PQ折叠,点A的对应点是点A'.当CA'的长度最小时,CQ的长为              ( A )

A.7 B.6 C.5 D.6.5

二、填空题(本大题有3个小题,共12分.17~18小题各3分;19小题有3个空,每空2分)

17.式子有意义,则x的取值范围为　x>2　. 

18.由六个边长相等且形状完全相同的菱形组成如图所示的网格,菱形的顶点称为格点,O,A,B,C都在格点上,∠AOB=60°,则sin∠ABC= 　. 

19.如图,☉O的直径AB的长为10,点C为直径AB上方半圆上一动点(不与点A,B重合),连接AC,BC,CD平分∠ACB交☉O于点D,AE平分∠CAB交CD于点E,连接BE,AD,BD.

(1)AC·BC的最大值为　50　; 

(2)AC+BC的最大值为　10　; 

(3)△ABE的外接圆的半径为　5　. 

20.(本小题满分8分)

已知“▲”和“■”分别表示0,1,2,3,4,5,6,7,8,9中的一个数字,例如:“■▲”表示个位数是“▲”、十位数是“■”的两位数;“3■”表示个位数是“■”、十位数是“3”的两位数.

(1)当“▲=■”时,若7■-▲2=14,求“▲”和“■”表示的数字;

(2)当“▲≠■”时,若多项式“■x2-▲”可以利用平方差公式在有理数范围内因式分解,且两位数“▲■”是完全平方数,求“▲”和“■”表示的数字.

解:(1)令“▲”=“■”=y,

则7×10+y-(10y+2)=14,解得y=6,

故“▲”和“■”表示的数字是6. (3分)

(2)∵多项式“■x2-▲”可以利用平方差公式在有理数范围内分解因式,

∴“▲” 和“■”分别表示1,4,9中的一个数字. 

又∵“▲”≠“■”,且两位数“▲■”是完全平方数,

∴“▲”表示4,“■”表示9. (8分)

21.(本小题满分8分)

问题探究:

已知ab=1,求证:+=1.

(1)淇淇是这样证明的:+===1.她的同桌嘉嘉发现,若将中的1代换成ab,则问题也可迎刃而解,请你帮嘉嘉完成证明过程.

方法应用:

(2)已知ab=1,请你根据嘉嘉的思路求+的值.

(1)证明:+=+=+=1. (4分)

(2)解:+=+=+=1. (8分)

22.(本小题满分9分)

如图,直线l1:y=3x-1与y轴交于点A,直线l2经过点B(-1,4),与直线l1相交于点P(1,b),并分别与x轴、y轴相交于点C,E.

(1)求b的值及直线l2的函数解析式;

(2)连接AB,求△PAB的面积;

(3)当反比例函数y=的图象与线段BC有公共点时,请直接写出k的最大值和最小值.

解:(1)∵直线l1:y=3x-1过点P(1,b),

∴b=3×1-1=2. (1分)

设直线l2的函数解析式为y=mx+n,

由直线l2过点B(-1,4),P(1,2),

可得解得

故直线l2的函数解析式为y=-x+3. (3分)

(2)对于直线l1:y=3x-1,当x=0时,y=-1,

∴A(0,-1).

对于直线l2:y=-x+3,当x=0时,y=3,∴E(0,3),

∴S△PAB=S△PAE+S△BAE=×4×1+×4×1=4. (7分)

(3) k的最大值为,最小值为-4. (9分)

解法提示:当反比例函数y=的图象与线段BC有公共点时,分以下两种情况讨论.

①若k<0,则当x=-1时,y≤4,即-≤4,

∴k≥-4,

故此时k的取值范围是-4≤k<0.

②若k>0,则令=-x+3,

整理,得x2-3x+k=0,

∴Δ=9-4k≥0,解得k≤,

故此时k的取值范围是0<k≤.

综上所述,k的最大值为,最小值为-4.

23.(本小题满分9分)

如图,在等边三角形ABC中,AC=6,点O在AC上,且AO=2,点P从点B出发,沿BA运动至点A停止,连接OP,以点O为圆心、OP为半径作圆.

(1)当☉O经过点A,且点A,P不重合时,求BP的长;

(2)当☉O经过BC上的点D,且∠DOP=60°时,求证:BC与☉O相切于点D;

(3)已知点I是△AOP的内心,连接OI,AI,在点P从☉O与BC相切运动到☉O第一次经过点A的过程中,求∠AIO度数的取值范围.

　　　　　　　　　备用图(1) 　　　备用图(2)

(1)解:当☉O经过点A,且点A,P不重合时,如图(1).

∵OA=OP,∠A=60°,

∴△OAP是等边三角形,

∴AP=OA=2,

∴BP=6-2=4. (2分)

图(1)　　图(2)

(2)证明:如图(2).

∵∠DOP=60°,∴∠AOP+∠COD=120°.

又∠C=60°,∴∠COD+∠CDO=120°,

∴∠CDO=∠AOP.

又∠A=∠C=60°,OD=OP,

∴△COD≌△APO,

∴CD=OA=2.

过点O作OE⊥BC于点E,则CE=OC·cos C=2,

∴点D与点E重合,

∴OD⊥BC,

∴☉O与BC相切于点D. (5分)

(3)过点A作AF⊥BC于点F,易知点I在AF上运动.

当☉O与BC相切时,如图(3).

由(2)易知∠AOP=∠ODC=90°,

∴∠AOI=∠AOP=45°.

∵∠CAB=60°,

∴∠OAI=∠CAB=30°,

∴∠AIO=180°-30°-45°=105°.

图(3)　　图(4)

当☉O第一次经过点A时,如图(4),易得∠AIO=120°.

综上可知,∠AIO度数的取值范围为105°≤∠AIO≤120°. (9分)

24.(本小题满分10分)

六一期间,某儿童玩具经销商开展“买玩具返现金”促销活动,活动规定购买一件某款玩具返还现金x(元).根据往年活动经验可知,六一期间该玩具的日销售量y(件)与返还现金x之间的函数关系为y=x+40,返还现金后,销售每件该款玩具的利润z(元)与x之间的函数关系为z=-x+30.

(1)若销售一件该款玩具返还顾客30元,则六一期间销售这款玩具的总利润为多少元?

(2)在确保销售该款玩具不亏本的情况下,求日销售量y的最大值,以及此时购买每件该款玩具返还顾客的金额.

(3)当返还的金额为多少时,经销商可获得最大日销售利润,最大日销售利润是多少?

解:(1)根据题意,可知六一期间销售这款玩具的总利润为(30+40)×(-×30+30)=1 680(元). (2分)

(2)易知随着x增大,y也增大,但z会减小.

要确保销售不亏本,则z≥0,即-x+30≥0,

解得x≤150,

∴当x=150时,y最大,

将x=150代入y=x+40,得y=190.

即当返还金额为150元时,销售量最大,最大值为190件. (6分)

(3)设日销售利润为w元,

则w=yz=(x+40)(-x+30)=-(x-55)2+1 805.

∵-<0,

∴当x=55时,w取最大值,最大值为1 805.

答:当返还的金额为55元时,经销商可获得最大日销售利润,最大日销售利润是1 805元. (10分)

25.(本小题满分10分)

如图,在▱ABCD中,AB=8,AD=8,BD⊥AB.点P为射线CD上一动点,连接BP,以BP为直径作☉O,交边AD(不含端点)于点Q,连接PQ,BQ.

(1)填空:当点P与点D重合时,BQ=　4　; 

(2)当的长度为时,求CP的长度;

(3)连接CQ,当圆心O恰好落在线段CQ上时,请直接写出CP的长度.

备用图

解:(1)4 (2分)

解法提示:∵AB=8,AD=8,BD⊥AB,

∴BD==8,∴△ABD是等腰直角三角形.

∵BP为☉O的直径,∴∠BQP=90°,

∴当点P与点D重合时,BQ⊥AD,∴BQ=AD=4.

(2)连接OQ.易知∠ADB=45°.

∵四边形ABCD为平行四边形,∴AB∥CD,

∴∠PDB=∠ABD=90°,∴点D在☉O上,

∴∠BOQ=2∠BDQ=90°,∴=·BO=,

∴BO=5,∴BP=2BO=10. 

在Rt△BDP中,BD=8,∴PD===6.

当点P在点D的右侧时,CP=CD-DP=2;

当点P在点D的左侧时,CP=CD+DP=14.

故CP的长度为2或14. (8分)

(3)8. (10分)

解法提示:连接OQ,易知直线OQ垂直平分线段BP.

又∵点O在线段CQ上,

∴点C在线段BP的垂直平分线上,∴CP=BC=AD=8.

26.(本小题满分12分)

已知抛物线L1:y=ax2-4ax,其顶点为P.

(1)试说明无论a为何值,抛物线L1恒过两个点,并求出这两个点的坐标.

(2)抛物线L2:y=x2-x+c与y轴交于点B,顶点记为Q,记抛物线L1与x轴正半轴的交点为A.

①当a<0,x的取值范围为 ≤x≤2(带不带等号 

　均可)　时,抛物线L1与L2均是y随x的增大而增大; 

②当BQ∥AP时,求a的值;

③若a=-1,H,G是抛物线L1上的两点,且点H,G的横坐标分别是-1,3,那么当抛物线L2与抛物线L1上点H,G之间的曲线(包含端点H,G)只有一个公共点时,请直接写出c的取值范围.

解:(1)令y=0,则ax2-4ax=0,易知a≠0,

∴x2-4x=0,解得x1=0,x2=4,

故无论a为何值,抛物线L1恒过点(0,0),(4,0). (2分)

(2)①≤x≤2(带不带等号均可) (4分)

解法提示:易知抛物线L1与L2的对称轴分别为直线x=2和直线x=,

对于抛物线L1,当x≤2时,y随x的增大而增大;

对于抛物线L2,当x≥时,y随x的增大而增大.

故x的取值范围为≤x≤2.

②易知B(0,c),A(4,0).

将x=代入y=x2-x+c,得y=c-,∴Q(,c-).

将x=2代入y=ax2-4ax,得y=-4a,∴P(2,-4a).

设直线BQ的解析式为y=kx+b,

将点B,Q的坐标分别代入,得

解得故直线BQ的解析式为y=-x+c.

同理可得直线AP的解析式为y=2ax-8a.

∵BQ∥AP,

∴2a=-,∴a=-. (9分)

③c=或-7≤c<-3. (12分)

解法提示:当a=-1时,y=ax2-4ax=-x2+4x,令x=-1,得y=-5;令x=3,得y=3,

图(1)

故H(-1,-5),G(3,3).

当抛物线L1与抛物线L2只有一个公共点时,如图(1).

令x2-x+c=-x2+4x,

整理,得2x2-5x+c=0,

当Δ=0时,25-8c=0,解得c=,

∴2x2-5x+=0,

解得x1=x2=,-1<<3,符合题意.

当抛物线L2过点G时,如图(2).

易得c=-3,此时抛物线L2与抛物线L1上点H,G之间的曲线(包含端点H,G)有2个公共点.

图(2)　　图(3)

当抛物线L2过点H时,如图(3).

易得c=-7,此时抛物线L2与抛物线L1上点H,G之间的曲线(包含端点H,G)有1个公共点.

而当-7≤c<-3时,抛物线L2与抛物线L1上点H,G之间的曲线(包含端点H,G)有1个公共点.

综上所述,c=或-7≤c<-3.