人教版七年级下册6.3 实数评课课件ppt

这是一份人教版七年级下册6.3 实数评课课件ppt，共27页。PPT课件主要包含了学习目标，旧知回顾，什么是立方根，什么是开立方，复习回顾，有限小数，无限循环小数，探究新知，运用新知，有理数等内容，欢迎下载使用。

1.了解实数的意义，并能将实数按要求进行准确的分类；2.熟练掌握实数大小比较方法；（重点）3.了解实数和数轴上的点一一对应，能用数轴上的点表示无理数.（难点）
如果一个数的立方等于a，那么这个数就叫做a的立方根．也叫做三次方根
求一个数a的立方根的运算，叫做开立方.
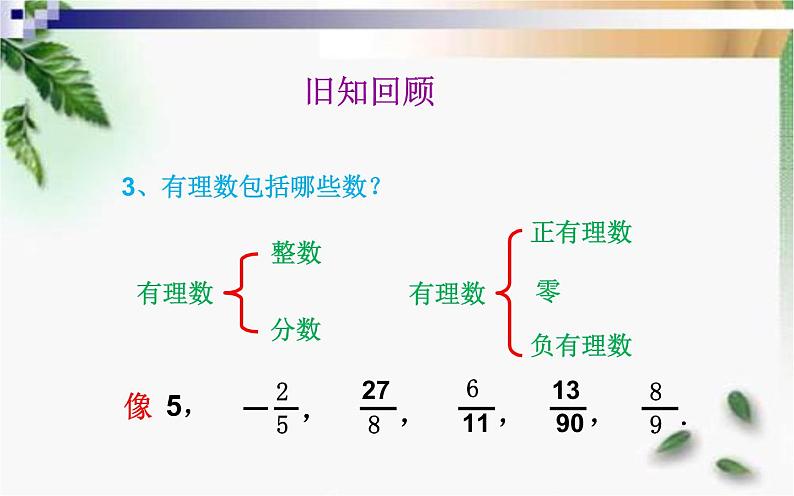
3、有理数包括哪些数？
把下列各数写成小数的形式：
整数和分数统称为有理数
有限小数和无限循环小数叫有理数
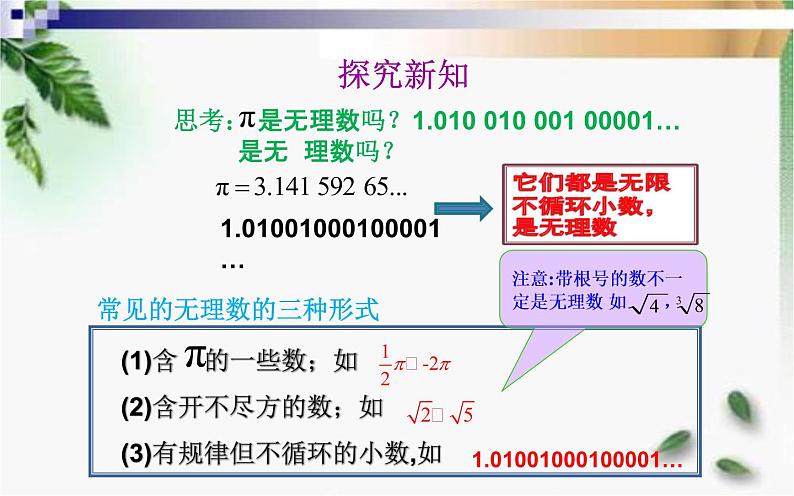
无限不循环小数叫无理数
1.01001000100001…
常见的无理数的三种形式
例1、下列各数中，哪些是有理数，哪些是无理数？
在以前的学习中，我们知道，分数和整数统称为有理数
那么在引入“无理数”后，我们所学过的所有数有新的统称吗？
初中阶段对数的认识范围扩充为
有理数和无理数统称实数
有限小数或无限循环小数
你还有其它分类方法吗？
把两个边长为1的小正方形通过剪、拼，得到一个大正方形，大正方形的边长为 从而说明边长为1的小正方形的对角线为 。
（1）如下图，以一个单位长度为边长画一个正方形,以原点为圆心,正方形对角线为半径画弧,与正、负半轴的交点分别为点A和点B，数轴上A点和B点对应的数是什么？
（2）如果将所有有理数都标到数轴上，那么数轴填满吗？
每一个实数都可以用数轴上的一个点来表示；反过来，数轴上的每一点都表示一个实数。
数轴上的点有些表示有理数，有些表示无理数.
实数与数轴上的点是一一对应的。
事实上，每一个无理数都可以用数轴上的一个点来表示出来。
直径为1个单位长度的圆从原点沿数轴向右滚动一周，圆上的一点由原点到达O′，点O′所对应的数是多少？
0 1 2 3 4
无理数π可以用数轴上的点表示
每一个有理数都可以用数轴上的点表示；每一个无理数都可以用数轴上的点表示； 数轴上的点有些表示有理数，有些表示无理数。 每一个实数都可以用数轴上的一个点来表示；反过来，数轴上的每一点都表示一个实数。 即实数和数轴上的点是一一对应的。 在数轴上的两个点，右边的点表示的实数总比左边的点表示的实数大。
实数与数轴上点一一对应
例题2、把下列各数填入相应的集合内：①有理数集合：｛ …｝；②无理数集合：｛ …｝；③正实数集合：｛ …｝；④负实数集合：｛ …｝．
例3 在数轴上表示下列各点，比较它们的大小， 并用“<”连接它们.
例4 估计 位于（ ）
A.0~1之间 B.1~2之间 C.2~3之间 D.3~4之间
熟记一些常见数的算术平方根；或用计算器估计.
例4 比较下列各组数的大小：
1.下列说法正确的是（ ）A. a一定是正实数 B. 是有理数C. 是有理数 D. 数轴上任一点都对应一个有理数
2.有一个数值转换器，原理如下，当输x=81时，输出的y是 （ ）
A.9 B.3 C. D.±3
3.判断快枪手——看谁最快最准！
（1）实数不是有理数就是无理数. （ ）
（2）无理数都是无限不循环小数. （ ）
（4）无理数都是无限小数. （ ）
（3）带根号的数都是无理数. （ ）
（5）无理数一定都带根号. （ ）
4.把下列各数填入相应的括号内：
2.实数的两种分类方法：
3.实数与数轴上的点成一一对应关系
通过本节课的学习，你觉得自己有哪些收获愿意和同学们一起分享呢？
无理数：无限不循环小数又叫做无理数
实数：有理数和无理数统称为实数
①根据实数的定义 ②根据实数的正负性
习题6.3：第2题 第3题 第6题