


初中数学人教版八年级下册17.1 勾股定理图片课件ppt
展开下图是在北京召开的2002年国际数学家大会(TCM-2002)的会标,其图案正是“弦图”,它标志着中国古代的数学成就.
相传2500年前,古希腊著名数学家毕达哥拉斯从朋友家的地砖铺成的地面上,发现了直角三角形的三边之间的某种数量关系.同学们,我们也来观察下面的地面, 看看你能发现什么?是否也和大数学家有同样的发现呢?
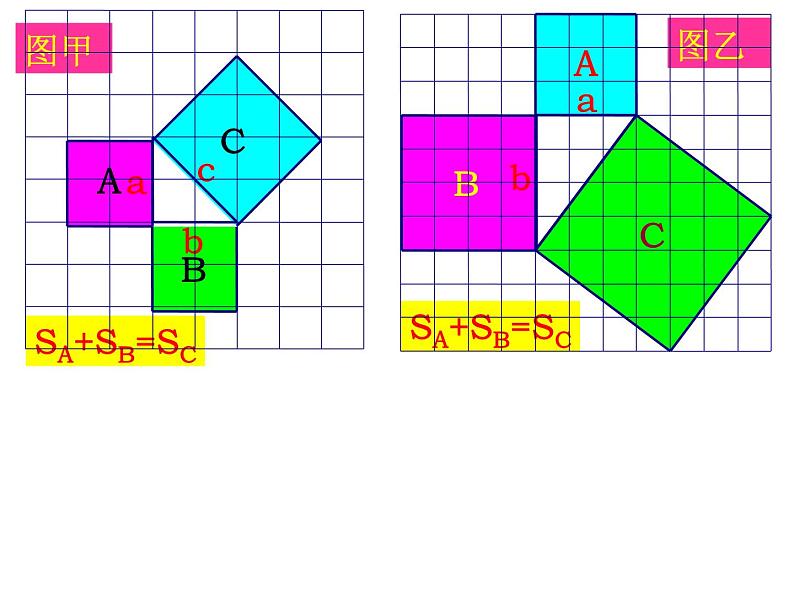
请大家从面积的角度来观察图形:
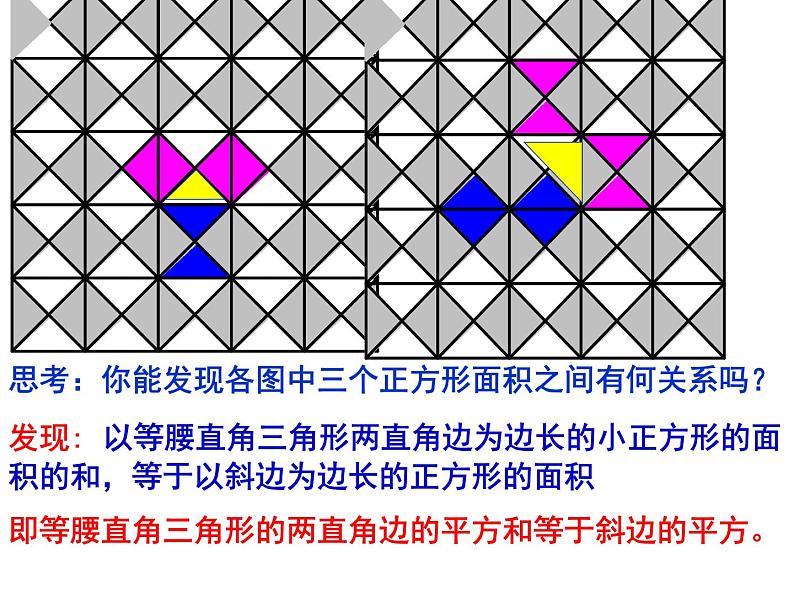
思考:你能发现各图中三个正方形面积之间有何关系吗?
发现: 以等腰直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的正方形的面积
即等腰直角三角形的两直角边的平方和等于斜边的平方。
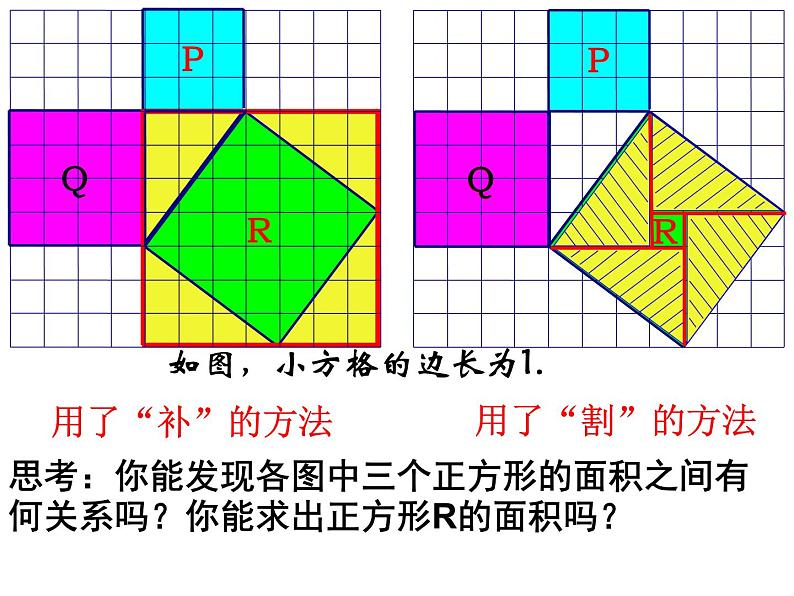
如图,小方格的边长为1.
思考:你能发现各图中三个正方形的面积之间有何关系吗?你能求出正方形R的面积吗?
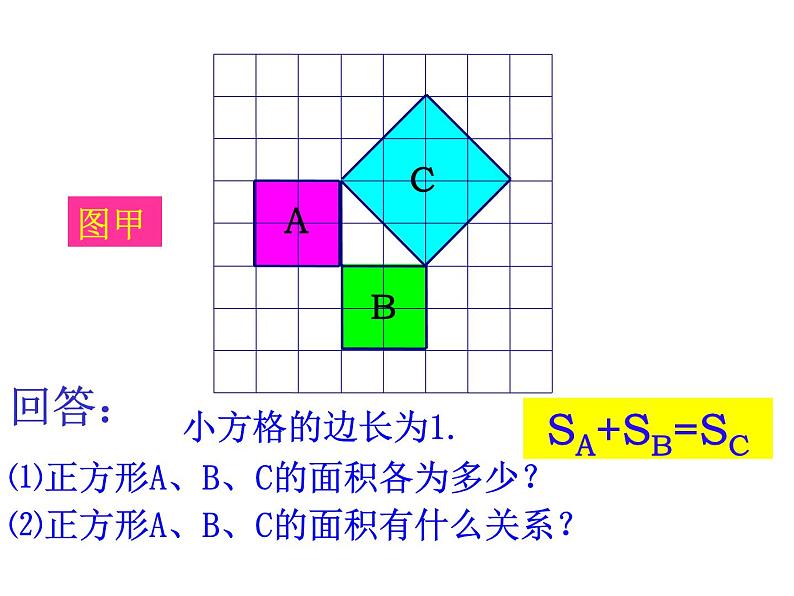
⑴正方形A、B、C的面积各为多少?
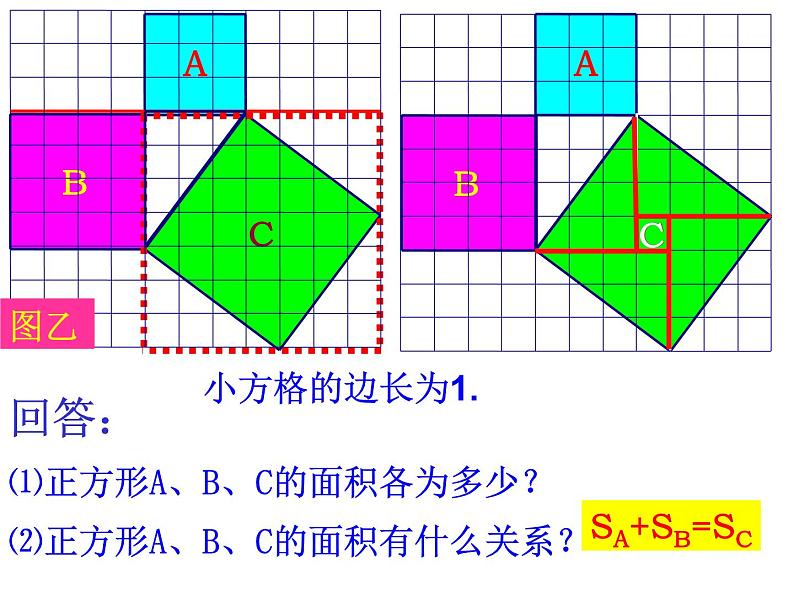
⑵正方形A、B、C的面积有什么关系?
⑴正方形A、B、C的面积各为多少?
3.猜想a、b、c 之间的关系?
即:直角三角形两直角边的平方和等于斜边的平方
命题1:如果直角三角形的两直角边长分别为a、b,斜边长为c,那么a2+b2=c2。
你能证明这个命题是正确的命题吗?
1、准备四个全等的直角三角形(设直角三角形的两条直角边分别为a,b,斜边c);
2、你能用这四个直角三角形拼成一个正方形吗?拼一拼试试看
3、你拼的正方形中是否含有以斜边c为边的正方形?
4、你能否就你拼出的图说明a2+b2=c2?
∴ c2=b2-2ab+a2+2ab
∴ a2+b2=c2
大正方形的面积可以表示为 ;也可以表示为
∴ a2+2ab+b2 =2ab+c2
在中国古代,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”.我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。
我国有记载的最早勾股定理的证明,是3世纪我国汉代代数学家赵爽在他所著的《勾股圆方图注》中,用四个全等的直角三角形拼成一个中空的正方形来证明的。
每个直角三角形的面积叫朱实,中间的正方形面积叫黄实,大正方形面积叫弦实,这个图也叫弦图。
两千多年前,古希腊有个毕达哥拉斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派,1955年希腊曾经发行了一枚纪念邮票。
定 理 的 历 史 及 证 明
★ 公元前600年左右,古希腊的毕达哥拉斯学派发现勾股定理,命名为“毕达哥拉斯定理” (百牛定理)(驴桥定理),而且给出了证明。
★ 古巴比仑人在公元前19世纪也发现此定理。
★ 定理从提出到现在的两千多年中,已经找到证明400多种,由鲁密斯搜集整理的《毕达哥拉斯》一书中就给出370种不同证法。
★ 公元前11世纪,周公与商高的对话(记录于公元前1世纪《周髀算经》)中提出“勾三、股四、弦五”。——勾股定理、商高定理
勾股定理有着悠久的历史,几乎所有具有古代文化的民族和国家都对勾股定理有所了解,它来源于人们生产实践之中,对人类发展起着十分重要的作用。
我国著名数学家华罗庚曾建议“发射”一种勾股定理的图形到宇宙中,如果宇宙有人的话,他们一定会认识这种语言的。这条建议得到许多科学家的赞同。
c2 = a2 + b2
直角三角形两直角边的平方和等于斜边的平方。
a2 = c2 - b2
b2 = c2 -a2
注意:1、只有在直角三角形中,才能用勾股定理
2、一般情况下,a、b代表直角边,c代表斜边。
3、直角三角形中,已知任意两边可以求出第三边。
例1:求出下列直角三角形中未知边的长度
例2、已知Rt△ABC中,∠C=900,(1)已知a=b=6,求c。(2)已知a=9,c=41,求b.(3)已知a:c=3:5,b=12,求a、c.(4)已知∠A=300,a=5cm,求b、c(5)已知∠A=300,b=5cm,求a、c
1. 一个直角三角形的两边长3cm、5cm,求第三边长。
2. 一高为2.5米的木梯,架在高为2.4米的墙上(如图),这时梯脚与墙的距离是多少?
3.求下列直角三角形中未知边的长:
4、求出下列直角三角形中未知的边.
①在解决上述问题时,每个直角三角形需知道几个条件?
②直角三角形哪条边最长?
想一想:
小明妈妈买了一部29英寸(74厘米)的电视机,小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了。你同意他的想法吗?你能解释这是为什么吗?
6.如图,因受台风影响,一棵树在离地面4米处断裂,树的顶部落在离树跟底部3米处,这棵树折断前有多高?
7.求下列图中表示边的未知数x、y、z的值.
1、本节课我们经历了怎样的探究过程?
2、本节课我们学到了什么?
3、学了本节课后我们有什么感想?
从特殊----- 一般的探究过程
勾股定理 割补法 以形解数法
中国悠久的文化和伟大的古代文明
4. 勾股定理是几何中最重要的定理之一,它揭示了直角三角形三边之间的数量关系.
1.勾股定理: 直角三角形两直角边a、b平方和等于斜边c平方。
3.利用勾股定理,在直角三角形中,已知任意两边求第三边的长。
2. 直角三角形两直角边上的正方形的面积和等于斜边上的正方形的面积。
初中数学人教版八年级下册17.1 勾股定理教学演示ppt课件: 这是一份初中数学人教版八年级下册17.1 勾股定理教学演示ppt课件,文件包含SectionBpptx、SectionA-1ppt、SectionA-2pptx、SelfCheckppt、SectionA1bmp3、SectionA2amp3、SectionA2bmp3、SectionA2dmp3、SectionB1cmp3、SectionB1dmp3、SectionB2bmp3、wordsandexpressionsUnit2mp3等12份课件配套教学资源,其中PPT共143页, 欢迎下载使用。
初中数学沪科版八年级下册18.1 勾股定理完美版课件ppt: 这是一份初中数学沪科版八年级下册18.1 勾股定理完美版课件ppt,共25页。PPT课件主要包含了a2+b2c2,c13,a20,Sa2+b2,即c2a2+b2等内容,欢迎下载使用。
苏科版八年级上册第三章 勾股定理3.1 勾股定理教学课件ppt: 这是一份苏科版八年级上册第三章 勾股定理3.1 勾股定理教学课件ppt,共17页。PPT课件主要包含了知识要点,勾股定理,SP+SQSR,∵S大正方形=c2,赵爽弦图,b-a,几何语言,练一练,cm²等内容,欢迎下载使用。













