初中数学第四章 因式分解1 因式分解一等奖ppt课件

这是一份初中数学第四章 因式分解1 因式分解一等奖ppt课件，共22页。PPT课件主要包含了导入新课，复习引入，讲授新课，探究引入，议一议，再深入理解，整式乘法，因式分解，x2-2x，x2-y2等内容，欢迎下载使用。

●教学重点1.理解掌握因式分解的意义.会判断一个变形是否为因式分解.（重点）
●教学难点2.通过观察，理解识别因式分解与整式乘法之间的联系与区别.（难点）
问题1：大家会计算（a+b）（a－b）吗？
答：会.（a+b）（a－b）=a2－b2..
问题2：a2－b2=（a+b）（a－b）是否成立呢？
答：能从等号右边推出等号左边，因为多项式 a2－b2与（a+b）（a－b）既然相等，那么 两个式子交换一下位置还成立.
思考：a2－b2=（a+b）（a－b）是成立的， 那么如何去推导呢？
因 式 分 解
问题：993-99能被100整除吗？你是怎样想的？
其中有一个因数为100，所以，993-99能被100整除.
想一想: 993-99还能被哪些正整数整除?
问题：你能尝试把a3－a化成几个整式的乘积的形式吗？
所以，a3－a=a（a－1）（a+1）
比较：大家可以观察a3－a与993－99这两个代数式.
因 式 分 解
想一想: a3-a还能被哪些整式?整除
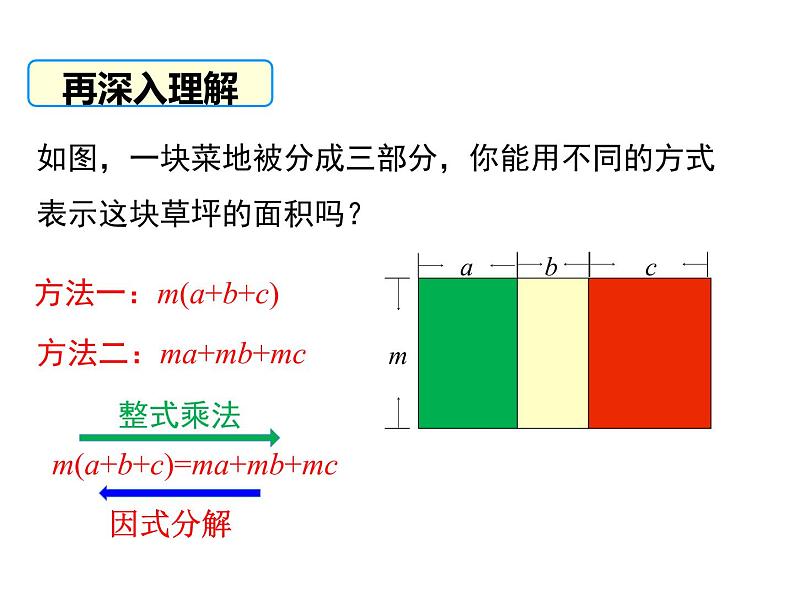
如图，一块菜地被分成三部分，你能用不同的方式表示这块草坪的面积吗？
方法一：m(a+b+c)
方法二：ma+mb+mc
m(a+b+c)=ma+mb+mc
完成下列题目：x(x-2)=_______(x+y)(x-y)=_______(x+1)2=________
根据左空，解决下列问题：x2-2x=( )( )x2-y2=( )( )x2+2x+1=( )2
联系：左右两式是同一多项式的不同表现形式.区别：左边一栏是多项式的乘法，右边一栏是把多项式化成了几个整式的积，他们的运算是相反的.
问题2：右边一栏表示的正是多项式的因式分解，你能根据我们的分析说出什么是因式分解吗？
问题1：观察同一行中，左右两边的等式有什么区别和联系？
把一个多项式化成几个整式的积的形式，这种变形叫做因式分解，也可称为分解因式.
其中，每个整式都叫做这个多项式的因式.
强调：1.因式分解是针对多项式的变形运算； 2.因式分解的结果是积的形式； 3.积中的每一个因式都是整式。
判断下列各式从左到右的变形中，是否为因式分解：
A. x(a﹣b)=ax﹣bx B. x2﹣1+y2=(x﹣1)(x+1)+y2 C. y2﹣1=(y+1)(y﹣1) D. ax+by+c=x(a+b)+c E. 2a3b=a2•2ab F. (x+3)(x﹣3)=x2﹣9
提示：判定一个变形是因式分解的条件：(1)左边是多项式．(2)右边是积的形式. (3)右边的因式全是整式.
根据左面算式填空:(1) 3x2-3x=_________(2)ma+mb+mc=___________(3) m2-16=__________(4) x2-6x+9=________ (5) a3-a=___________
计算下列各式:(1) 3x(x-1)= __,(2) m(a+b+c) = ______ ,(3)(m+4)(m-4)= _____,(4)(x-3)2= ,(5)a(a+1)(a-1)= __,
a(a+1)(a-1)
想一想：由a(a+1)(a-1)得到a3-a的变形是什么运算? 由a3-a得到a(a+1)(a-1)的变形与它有什么不同?
由a(a+1)(a-1)得到a3-a的变形是整式乘法,由a3-a得到a(a+1)(a-1)的变形与上面的变形互为逆过程.
x2-1 (x+1)(x-1)
x2-1 = (x+1)(x-1)
等式的特征：左边是多项式，右边是几个整式的乘积
想一想：整式乘法与因式分解有什么关系？
是互为相反的变形（互逆的），即
例 若多项式x2+ax+b分解因式的结果为a（x﹣2）（x+3），求a，b的值.
解：∵x2+ax+b=a（x﹣2）（x+3） =ax2+ax-6a. ∴a=1， b=﹣6a=﹣6.
方法归纳：对于此类问题，掌握因式分解与整式乘法为互逆运算是解题关键，应先把分解因式后的结果乘开，再与多项式的各项系数相对应比较即可.
下列多项式中， 分解因式的结果为-(x+y)(x-y)的是（　　） A．x2﹣y2 B．﹣x2+y2 C．x2+y2 D．﹣x2﹣y2
2. 下列从左到右的变形中，是因式分解的有______ .　①24x2y=4x•6xy ②（x+5）（x﹣5）=x2﹣25 ③x2+2x﹣3=（x+3）（x﹣1）④9x2﹣6x+1=3x（x﹣2）+1 ⑤x2+1=x（x+ ）⑥3xn+2+27xn=3xn（ x2+9）
1. 下列各式中从左到右的变形属于分解因式的是（　　）A. a(a+b-1)=a2+ab-a B. a2-a-2=a(a-1)-2C. -4a2+9b2=(-2a+3b)(2a+3b) D.2x +1=x(2+ )
3. 把多项式x2+4mx+5因式分解得(x+5)(x+n)，则m+n的值为 　 ．　
解析：由题意可得 x2+4mx+5=(x+5)(x+n) =x2+(n+5)x+5n， 5n=5，4m=n+5． 解得n=1，m= ， m+n=1+ = .
4. 20042+2004能被2005整除吗?
解: ∵20042+2004=2004(2004+1) =2004 ×2005 ∴ 20042+2004能被2005整除
5. 甲、乙两个同学分解因式x2+ax+b时，甲看错了b，分解结果为(x+2)(x+4)；乙看错了a，分解结果为(x+1）(x+9)，求a+b的值.
解：分解因式甲看错了b，但a是正确的， 其分解结果为x2+ax+b=(x+2)(x+4)=x2+6x+8， ∴a=6， 同理，乙看错了a，但b是正确的， 分解结果为x2+ax+b=(x+1)(x+9)=x2+10x+9， ∴b=9， ∴a+b=15．
6. 若多项式x4+mx3+nx﹣16含有因式(x﹣2)和(x﹣1)， 求mn的值.
解：∵x4+mx3+nx﹣16的最高次数是4， ∴可设x4+mx3+nx﹣16=(x-1)(x-2)(x2+ax+b)， 则x4+mx3+nx-16=x4+(a-3)x3+(b-3a+2)x2+(2a-3b)x+2b 比较系数得 2b=-16，b-3a+2=0，a-3=m，2a-3b=n 解得a=-2，b=-8，m=-5，n=20. ∴mn=﹣5×20=﹣100．
定义：把一个多项式化成几个整式的_____的形式，叫做因式分解，也可称为___________.
其中，每个整式叫做这个多项式的_______.
与多项式乘法运算的关系
的变形过程.
前者是把一个多项式化为几个整式的_____，后者是把几个整式的______化为一个_________.