初中数学3 分式的加减法优秀课件ppt

这是一份初中数学3 分式的加减法优秀课件ppt，共14页。PPT课件主要包含了最小公倍数，最简公分母，相同字母取最高次幂，单独字母不能丢，x+y2，x-y，x-5，x+5，x-5x+5，找最简公分母等内容，欢迎下载使用。

会找异分母分式的最简公分母会进行异分母分式的通分会用异分母分式加减法则进行运算
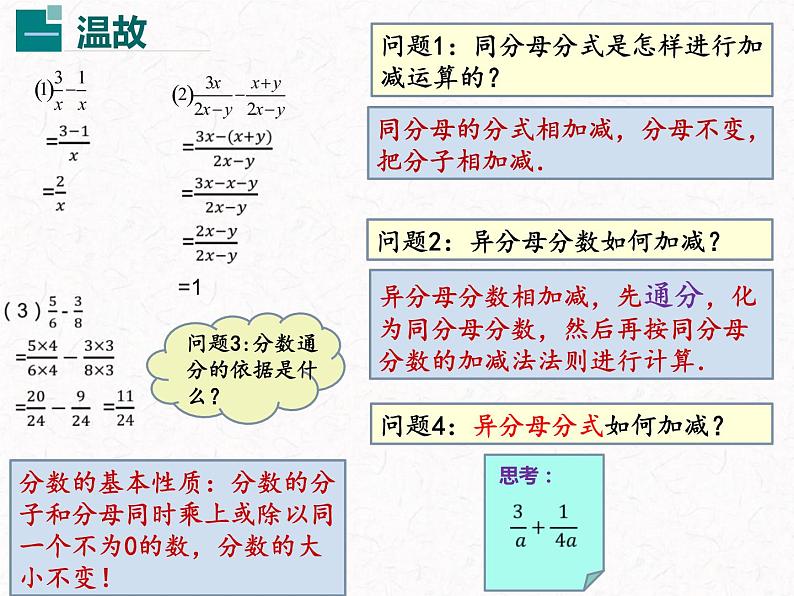
问题1：同分母分式是怎样进行加减运算的？
同分母的分式相加减，分母不变，把分子相加减．
问题2：异分母分数如何加减？
异分母分数相加减，先通分，化为同分母分数，然后再按同分母分数的加减法法则进行计算．
分数的基本性质：分数的分子和分母同时乘上或除以同一个不为0的数，分数的大小不变！
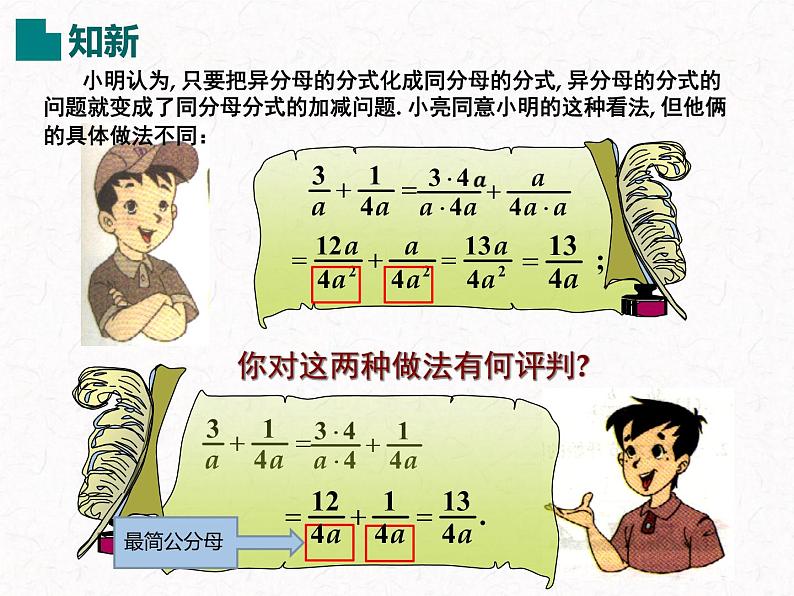
小明认为, 只要把异分母的分式化成同分母的分式, 异分母的分式的问题就变成了同分母分式的加减问题. 小亮同意小明的这种看法, 但他俩的具体做法不同：
你对这两种做法有何评判?
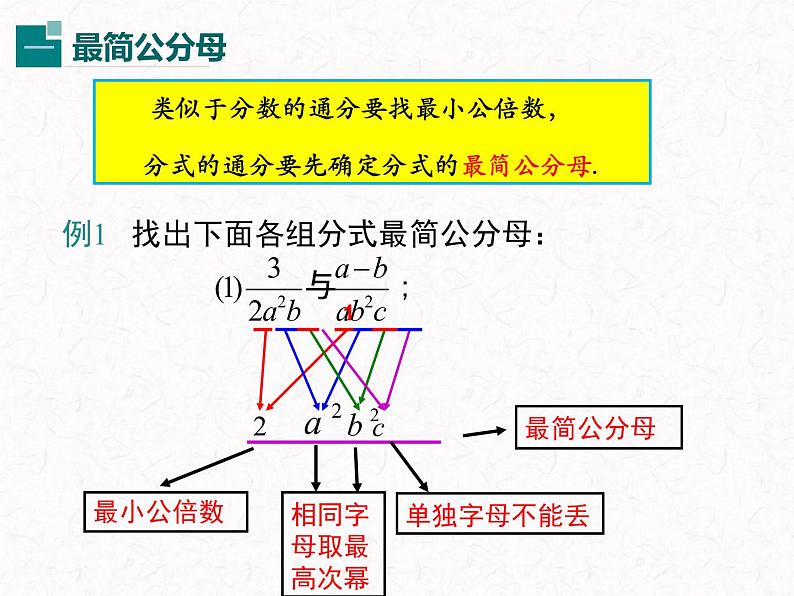
例1 找出下面各组分式最简公分母：
类似于分数的通分要找最小公倍数， 分式的通分要先确定分式的最简公分母.
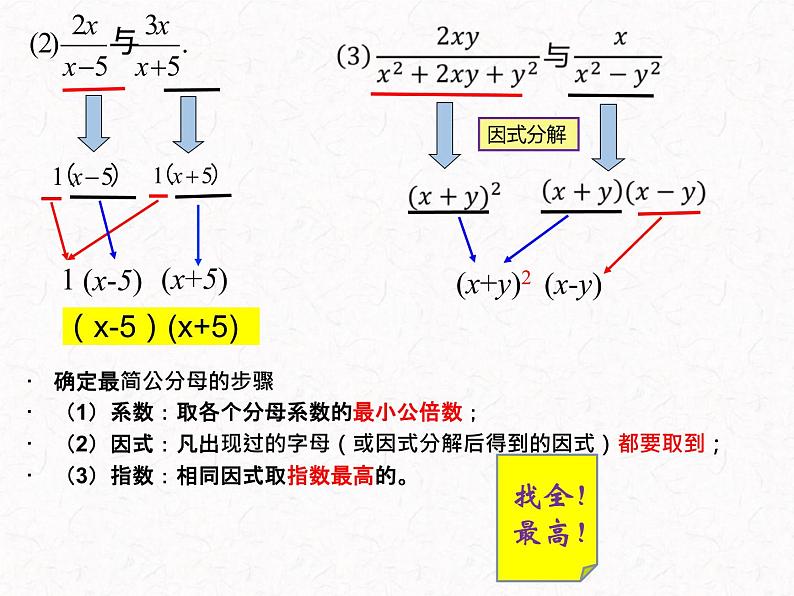
确定最简公分母的步骤（1）系数：取各个分母系数的最小公倍数；（2）因式：凡出现过的字母（或因式分解后得到的因式）都要取到；（3）指数：相同因式取指数最高的。
x(x-5)（x+5）
根据分式的基本性质，异分母分式可以化为同分母分式，这一过程称为分式的通分.
依据“分式的基本性质”，通过通分
异分母分式相加减，先通分，变为同分母的分式，再加减.
1异分母分式相加减，先通分，变为同分母的分式 , 再加减。2.如何确定最简公分母？（1）系数：取各个分母系数的最小公倍数；（2）因式：凡出现过的字母（或因式分解后得到的因式）都要取到；（3）指数：相同因式取指数最高的。