初中数学北师大版八年级下册3 线段的垂直平分线优秀ppt课件

这是一份初中数学北师大版八年级下册3 线段的垂直平分线优秀ppt课件，共19页。PPT课件主要包含了学习目标，线段垂直平分线上的点，到线段两端点距离相等，性质判定，垂直平分线的尺规作图，保证有交点，两条直线交于一点，三条直线交于一点，交点在第三条直线上，问题转化为等内容，欢迎下载使用。

01.探索并证明三角形三边垂直平分线的性质
02.能用尺规作出已知底边及底边上的高的等腰三角形
03.能用尺规过一点作已知直线的垂线
垂直平分线的性质与判定
∵ 直线MN垂直平分AB， 且点P在直线MN上
到线段两端点距离相等的点
在这条线段的垂直平分线上
∴ 点P在AB的垂直平分线上
思考：利用判定证明线段的垂直平分线时，需找到几个点，为什么？
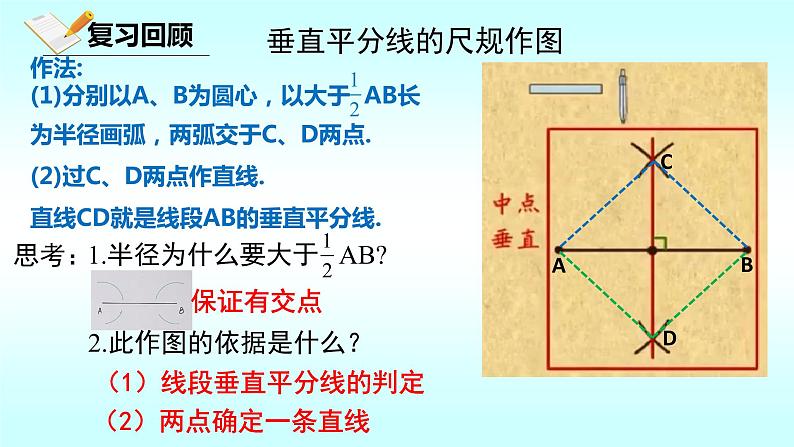
2.此作图的依据是什么？
（1）线段垂直平分线的判定
（2）两点确定一条直线
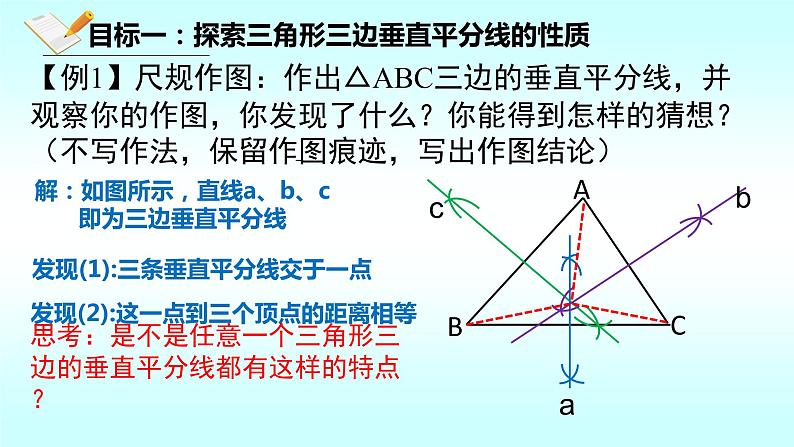
【例1】尺规作图：作出△ABC三边的垂直平分线，并观察你的作图，你发现了什么？你能得到怎样的猜想？ （不写作法，保留作图痕迹，写出作图结论）
解：如图所示，直线a、b、c 即为三边垂直平分线
发现(1):三条垂直平分线交于一点
发现(2):这一点到三个顶点的距离相等
思考：是不是任意一个三角形三边的垂直平分线都有这样的特点？
目标一：探索三角形三边垂直平分线的性质
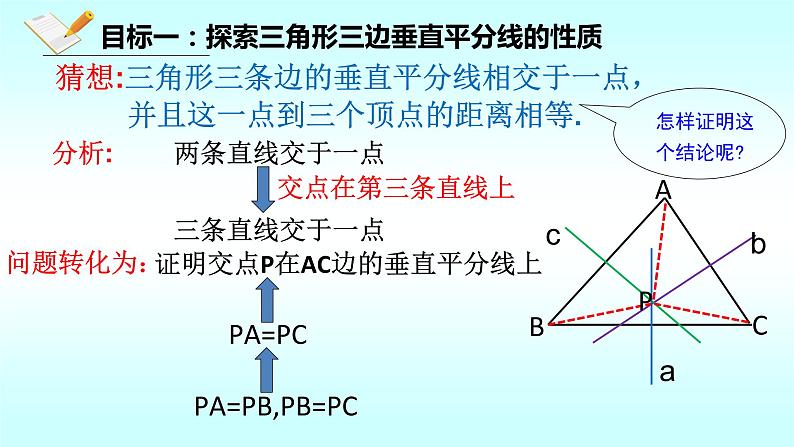
猜想:三角形三条边的垂直平分线相交于一点， 并且这一点到三个顶点的距离相等.
证明交点P在AC边的垂直平分线上
PA=PB,PB=PC
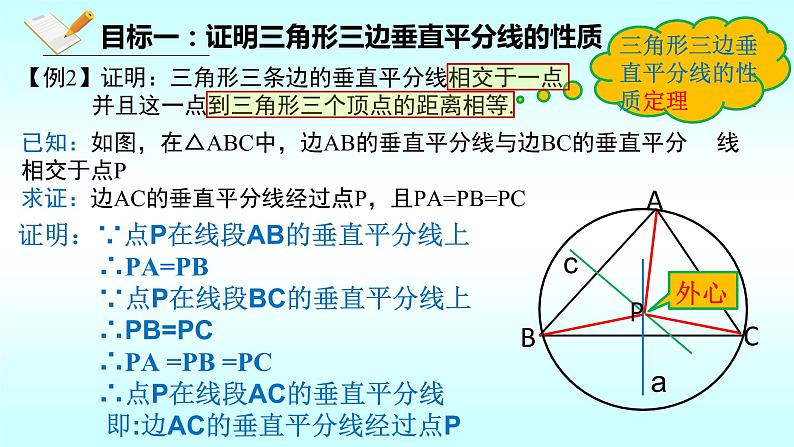
目标一：证明三角形三边垂直平分线的性质
已知：如图，在△ABC中，边AB的垂直平分线与边BC的垂直平分 线相交于点P求证：边AC的垂直平分线经过点P，且PA=PB=PC
【例2】证明：三角形三条边的垂直平分线相交于一点， 并且这一点到三角形三个顶点的距离相等.
证明：∵点P在线段AB的垂直平分线上 ∴PA=PB ∵点P在线段BC的垂直平分线上 ∴PB=PC ∴PA =PB =PC ∴点P在线段AC的垂直平分线 即:边AC的垂直平分线经过点P
为筹办一个大型运动会，某市政府打算修建一个大型体育中心.在选址过程中， 有人建议该体育中心所在位置应与该市的三个城镇中心（图中P，Q，R表示） 的距离相等.请根据上述建议，分别在图（1）图（2）中画出体育中心G的位置.
三角形三边垂直平分线的性质定理：三角形三条边的垂直平分线相交于一点，并且这一点到三角形三个顶点的距离相等.
锐角三角形内部（形内）
直角三角形斜边中点(形上)
钝角三角形外部（形外）
直角三角形三边中垂线交点在斜边中点
直角三角形任意一边中垂线与斜边相交，交点必为斜边中点
【例3】已知底边及底边上的高，求作等腰三角形 已知：线段a，h 求作：△ABC，使AB=AC，且BC=a，高AD=h。（不写作法，保留作图痕迹，写出作图结论）
h在BC的垂直平分线上
∴作BC的垂直平分线，并截取高h即可
目标二 尺规作出已知底边及底边上的高的等腰三角形
思考：1.作图依据？（1）（2）
2.你能做出几个满足上述条件的等腰三角形？它们有怎样的关系？
3.已知任意形状的三角形的一条边及这条边上的高，你能作出这个三角形吗? 如果能，能作出几个?所作出的三角形全等?
目标三 过一点作已知直线的垂线
目标三 用尺规过一点作已知直线的垂线
（2）作线段AB的垂直平分线m 则直线m垂直于l，且经过点P .
作法：（1）以P为圆心，以任意长为半 径画弧，交直线l于点A、点B；
（2）以P为圆心，以PK长为半径画弧，交直 线l于点A、点B；
（3）作线段AB的垂直平分线m 则直线m垂直于l，且经过点P .
三角形三边垂直平分线定理