北师大版八年级下册3 线段的垂直平分线优秀ppt课件

这是一份北师大版八年级下册3 线段的垂直平分线优秀ppt课件，共22页。PPT课件主要包含了新课导入，新课探究，可以画出无数个三角形，你明白这个作法吗，在三角形内，在斜边中点，在三角形外，这是个等腰直角三角形，课堂小结等内容，欢迎下载使用。

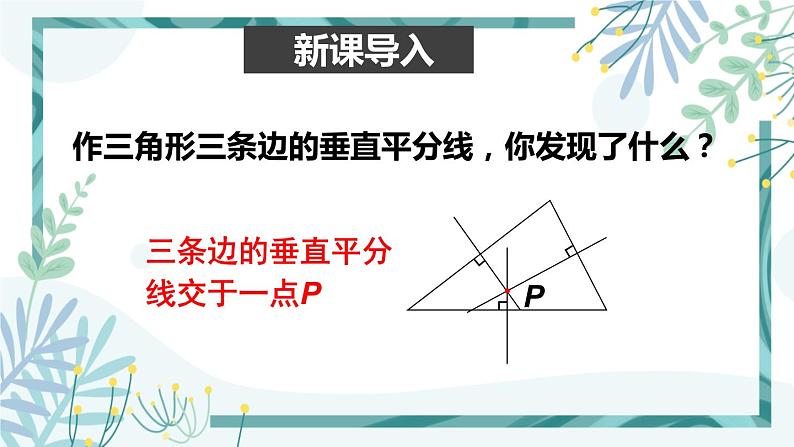
作三角形三条边的垂直平分线，你发现了什么？
三条边的垂直平分线交于一点P
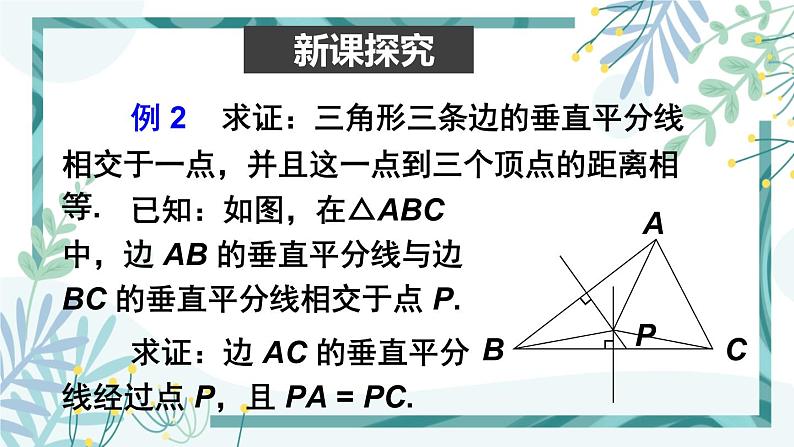
例 2 求证：三角形三条边的垂直平分线相交于一点，并且这一点到三个顶点的距离相等.
已知：如图，在△ABC 中，边 AB 的垂直平分线与边 BC 的垂直平分线相交于点 P.
求证：边 AC 的垂直平分线经过点 P，且 PA = PC.
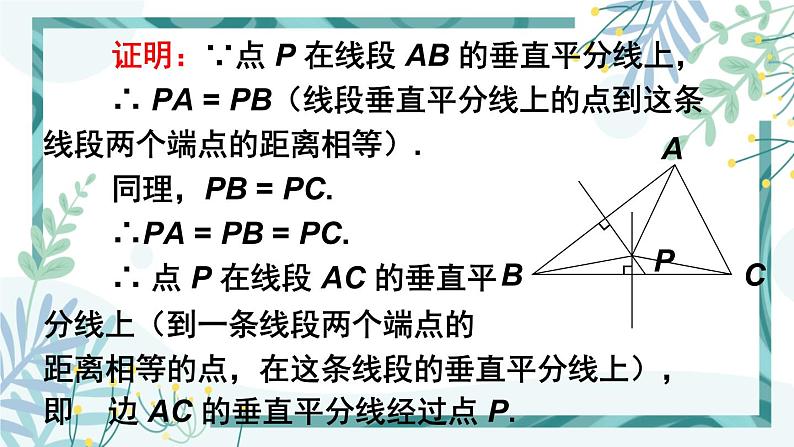
证明：∵点 P 在线段 AB 的垂直平分线上， ∴ PA = PB（线段垂直平分线上的点到这条线段两个端点的距离相等）. 同理，PB = PC. ∴PA = PB = PC. ∴ 点 P 在线段 AC 的垂直平分线上（到一条线段两个端点的距离相等的点，在这条线段的垂直平分线上），即 边 AC 的垂直平分线经过点 P.
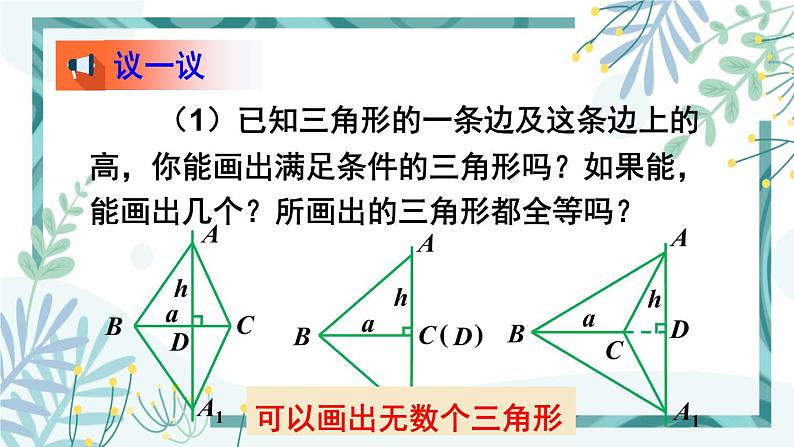
（1）已知三角形的一条边及这条边上的高，你能画出满足条件的三角形吗？如果能，能画出几个？所画出的三角形都全等吗？
（2）已知等腰三角形的底边，你能用尺规作出等腰三角形吗？如果能，能画出几个？所画出的三角形都全等吗？
（3）已知等腰三角形的底边及底边上的高，你能用尺规作出等腰三角形吗？能作几个？
这样的等腰三角形应该只有两个，并且它们是全等的，分别位于已知底边的两侧.
例 3 已知一个等腰三角形的底边及底边上的高，求作这个等腰三角形.
已知：如图，线段 a，h.
求作：△ABC，使 AB = AC，且 BC = a，高 AD = h.
作法： （1）作线段 BC = a. （2）作线段 BC 的垂直平分线 l，交 BC 于点 D. （3）在 l 上作线段 DA，使 DA = h. （4）连接 AB，AC. △ABC为所求的等腰三角形.
已知直线 l 和 l 上一点 P，用尺规作 l 的垂线，使它经过点 P.　
如果点 P 是直线 l 外一点，那么怎样用尺规作 l 的垂线，使它经过点 P 呢？说说你的作法，并与同伴交流.
1. 如图，在△ABC 中，已知 AC = 27，AB 的垂直平分线交 AB 于点 D，交 AC 于点 E，△BCE 的周长等于 50，求 BC 的长.
解：因为 DE 为 AB 的垂直平分线， 所以 AE = BE. △BCE的周长为 d = EC + BE + BC = EC + AE + BC = AC + BC = 27 + BC = 50. 所以 BC = 23 .
2. 分别作出直角三角形、锐角三角形、钝角三角形三边的垂直平分线，说明交点分别在什么位置.
3. 如图，在△ABC 中，BC = 2，∠BAC ＞ 90°，AB 的垂直平分线交 BC 于点 F ，请找出图中相等的线段，并求出△AEF 的周长.
解：AE = BE，AF = CF. （线段垂直平分线上的点到这条线段两个端点的距离相等）
∴ AE + EF + AF = BE + EF + CF = BC = 2
4. 如图，已知线段 a，求作以 a 为底边、以 a 为高的等腰三角形，这个等腰三角形有什么特征？
5. 已知：△ABC 中，AB = AC，AD 是 BC边一上的中线，AB 的垂直平分线交 AD 于 O. 求证：OA = OB = OC.
证明：∵AB = AC， AD 是 BC 的中线， ∴AD 垂直平分 BC（等腰三角形底边上的中线垂直于底边）. 又∵AB 的垂直平分线与交于点 O， ∴OB = OC = OA（三角形三条边的垂直平分线交于一点，并且这一点到三个顶点的距离相等）.
已知一个等腰三角形的底边及底边上的高，作这个等腰三角形：