初中数学华师大版八年级下册2. 一次函数的图象精品ppt课件

这是一份初中数学华师大版八年级下册2. 一次函数的图象精品ppt课件，共19页。PPT课件主要包含了学习目标，两点确定一条直线，确定两个点，复习引入，合作探究，典例精析，y-2x-3，归纳总结，取值范围，＞1500等内容，欢迎下载使用。

1.会求一次函数图象与两坐标轴的交点坐标，初步感悟函数与方程的关系；（重点）2.能正确画出具有实际意义的一次函数图象.（难点）
1.一次函数y=kx+b的图象是什么图形？
2.几个点可以确定一条直线？
y=kx+b的图象是一条直线
3.画一次函数图象时，只取几个点就可以了？
思考：你取的是哪几个点？和同学比较一下，怎样取比较简单.
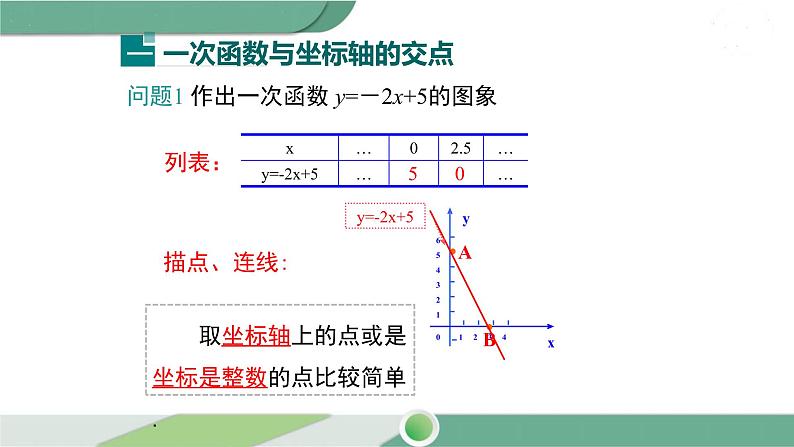
问题1 作出一次函数 y=－2x+5的图象
取坐标轴上的点或是坐标是整数的点比较简单.
一次函数 y = k x + b(k≠0)
(1) 当 x = 0 时, y =0 · k + b = b, 所以一次函数 y = k x + b 经过 ( 0 , b ) 点.
(2) 当 y = 0 时, k x + b = 0, x =
所以一次函数 y = k x + b 经过( , 0)点.
因为正比例函数是一次函数y=kx+b，当b=0时的特殊情况
所以正比例函数y=kx是经过（0,0）和（1,k）的一条直线，即正比例函数过原点.
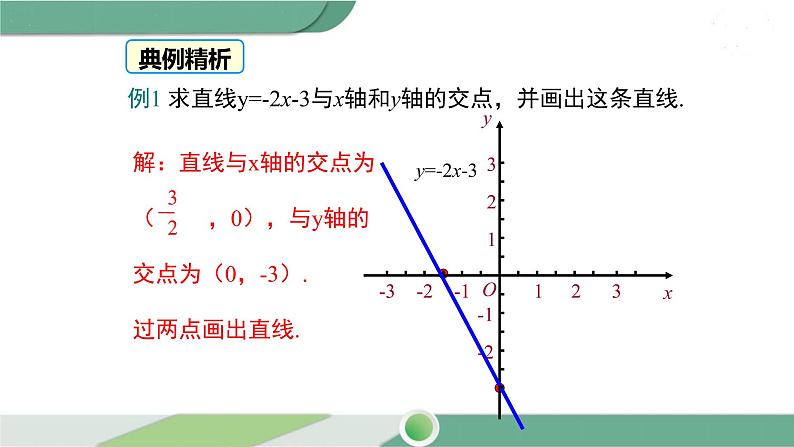
例1 求直线y=-2x-3与x轴和y轴的交点，并画出这条直线.
解：直线与x轴的交点为（ ，0），与y轴的交点为（0，-3）.过两点画出直线.
例2 如图，直线y＝2x＋3与x轴相交于点A，与y轴相交于点B.(1)求A，B两点的坐标；
解：(1)令y＝0，得x＝ ∴A点坐标为（ ，0）；令x＝0，得y＝3，∴B点坐标为(0，3)．
例2 如图，直线y＝2x＋3与x轴相交于点A，与y轴相交于点B.(2)过点B作直线BP与x轴相交于点P，且使OP＝2OA，求△ABP的面积．
(2)设P点坐标为(x，0)，依题意，得x＝±3.∴P点坐标为P1(3，0)或P2(－3，0)．∴S△ABP1＝ × ×3＝ ，S△ABP2＝ × ×3＝ .∴△ABP的面积为 或 .
直线y=kx+b（k≠0）与坐标轴的交点注意：|b|，| |是直线y＝kx＋b(k≠0)与坐标轴的两交点和原点构成的直角三角形的两直角边的长．
与x轴的交点坐标为（ ，0）与y轴的交点坐标为（0，b）方程kx+b=0的解是x=
问题2 2017年暑假小波同学带10元钱去文具店买笔芯，已知每根定价1元8角，写出买笔芯剩余的钱y(元)与买笔芯的数量x(根)之间的函数关系式，并画出函数的图象．
解：根据题意得函数关系式为y＝10－1.8x，x的范围是0≤x≤ 中的整数，故函数的图象为一条线段上间断的点.
例3 汽车距北京的路程s（千米）与汽车在高速公路上行驶的时间t（时）之间的函数关系式是s=570-95t，试画出这个函数的图象.
分析：在实际问题中，我们可以在表示时间的t轴和表示路程的s轴上分别选取适当的单位长度，画出平面直角坐标系.
当s=0时，t的值为6，又t≥0，所以自变量t的取值范围为 0≤t≤6.函数的图象是一条线段.
例4.今有一根弹簧，不悬挂重物时的长度为12cm，悬挂的重物每增加1kg(重物不超过8kg)，弹簧的长度就增加0.5cm.写出弹簧的长度y(cm)和悬挂物的质量x(kg)之间的函数关系式，指出自变量的取值范围，并画出这个函数的图象.
解:由题意，可得函数关系式为
自变量 x 的取值范围为0≤x≤8.函数图象如图：
例5.试说明无论m为何值，函数 y = (m+1) x + 2m﹣6的图象都过某一定点.
解：由y = (m+1) x + 2m﹣6，得
y -x+6= (x+2)m.
令y -x+6=0 ，x+2=0.
解得 x=-2 ，y=-8.
所以，无论m为何值，函数 y = (m+1) x + 2m﹣6的图象都过点(-2，-8).
一次函数y＝kx＋b(k≠0)的图象：当x≤a或x≥a时，函数y＝kx＋b的图象是射线；当a≤x≤c(a 一次函数的图象可能是一条直线，也可能是一条线段，还可能是一条射线，一条折线或离散的点，这全部取决于自变量的____________，因此在解题时应具体问题具体分析．
1.请画出函数y=x-1与函数y=-2x-1的图象.
2.某单位准备和一个体车主或一国营出租车公司中的一家签订月租车合同，设汽车每月行驶x 千米，个体车主收费y1元，国营出租车公司收费为y2元，观察下列图象可知，当x________时，选用个体车较合算．