数学九年级上册1 菱形的性质与判定优质ppt课件

这是一份数学九年级上册1 菱形的性质与判定优质ppt课件，共18页。PPT课件主要包含了学习目标，新课导入，新课讲解，课堂小结，当堂小练，拓展与延伸，布置作业等内容，欢迎下载使用。

1. 由对角线的位置关系判定菱形（重点、难点） 2. 由边的数量关系判定菱形
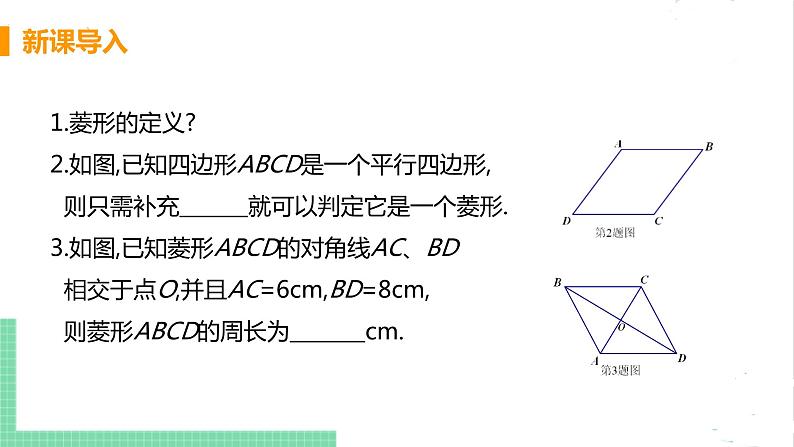
1.菱形的定义?2.如图,已知四边形ABCD是一个平行四边形, 则只需补充 就可以判定它是一个菱形.3.如图,已知菱形ABCD的对角线AC、BD 相交于点O,并且AC=6cm,BD=8cm, 则菱形ABCD的周长为 cm.
根据菱形的定义，有一组邻边相等的平行四边形是菱形．除此之外，你认为还有什么条件可以判断一个平行四边形是菱形？先想一想，再与同伴交流．
知识点1 由对角线的位置关系判定菱形
可以发现，对角线互相垂直的平行四边形是菱形．下面我们证明这个结论．
已知：如图，在 ABCD中，对角线AC与BD相交于点O，AC⊥BD. 求证： ABCD是菱形．
∵四边形ABCD是平行四边形，∴OA＝OC.又∵AC⊥BD，∴BD是线段AC的垂直平分线．∴BA＝BC.∴四边形ABCD是菱形(菱形的定义)．
已知线段AC，你能用尺规作图的方法作一个菱形ABCD，使AC为菱形的一条对角线吗？
1. 判定定理：对角线互相垂直的平行四边形是菱形.2. 规律导引：若用对角线进行判定：先证明四边形是平行四边形，再证明对角线互相垂直，或直接证明四边形的对角线互相垂直平分.
如图，▱ABCD的对角线AC，BD相交于点O，请你添加一个适当的条件__________使其成为菱形(只填一个即可)．
已知:如图,在□ABCD中,对角线AC⊥BD.
求证:四边形ABCD是菱形.
证明:∵四边形ABCD是平行四边形.∴AO=CO.∵AC⊥BD,∴ DA=DC.(线段垂直平分线上的点到线段两端点的距离相等)∴四边形ABCD是菱形.
知识点2 由边的数量关系判定菱形
已知线段AC，你能用尺规作图的方法作一个菱形ABCD，使AC为菱形的一条对角线吗？ 如图，分别以A，C为圆心，以大于 AC的长为半径作弧，两条弧分别相交于点B，D，依次连接A，B，C，D，四边形ABCD看上去是菱形．你是怎么做的？你认为小刚的做法正确吗？与同伴交流． 定理：四边相等的四边形是菱形. 请你完成这个定理的证明.
已知：如图，在 ABCD中，对角线AC与BD相交 于点O，AB ＝ ，OA＝2，OB＝1. 求证： ABCD 是菱形． 在△AOB中， ∵AB＝ ，OA＝2，OB＝1， ∴AB2＝AO2＋OB2. ∴△AOB是直角三角形，∠AOB是直角． ∴AC⊥BD. ∴ ABCD是菱形(对角线垂直的平行四边形是菱形)．
如图，在▱ABCD中，对角线AC与BD交于点O， 若增加一个条件，使▱ABCD成为菱形，下列给 出的条件不正确的是(　　) A．AB＝AD B．AC⊥BD C．AC＝BD D．∠BAC＝∠DAC
1.判定定理2：四边相等的四边形是菱形.2.规律导引：若用边进行判定：先证明四边形是平 行四边形，再证明一组邻边相等，或直接证明四 边形的四条边都相等．
1.菱形的判定方法： (1)(定义法)：一组邻边相等的平行四边形是菱形； (2)(对角线)：对角线互相垂直的平行四边形是菱形； (3)(边)：四边相等的四边形是菱形．
如图1-6，四边形ABCD是边长为13cm的菱形，其中对角线BD长10cm.求： （1）对角线AC的长度；（2）菱形ABCD的面积.