






初中6 完全平方公式优质课课件ppt
展开1.了解并掌握完全平方公式.(重点) 2.理解完全平方公式的推导过程,并会应用完全平方公式进行计算.(难点)
计算下列多项式的积,你能发现什么规律?
(1) (p+1)2=(p+1)(p+1)
(2) (m+2)2=(m+2)(m+2)
(3) (p-1)2=(p-1)(p-1)
(4) (m-2)2=(m-2)(m-2)
知识点1 完全平方公式
(1) 用多项式乘法推导完全平方公式
=(a+b)(a+b)=a2+ab+ab+b2=a2+2ab+b2
=(a-b)(a-b)=a2-ab-ab+b2=a2-2ab+b2
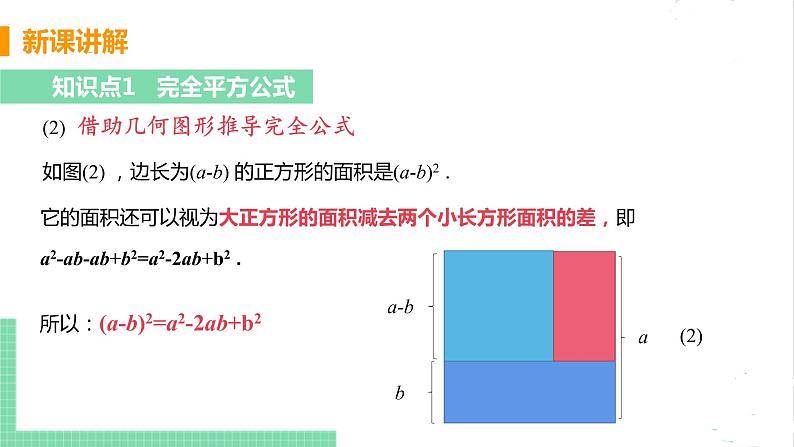
(2) 借助几何图形推导完全公式
如图(1) ,边长为(a+b) 的正方形的面积是(a+b)2 .
它的面积还可以视为两个小正方形和两个小长方形面积的和,即a2+ab+ab+b2=a2+2ab+b2 .
所以:(a+b)2=a2+2ab+b2
它的面积还可以视为大正方形的面积减去两个小长方形面积的差,即a2-ab-ab+b2=a2-2ab+b2 .
如图(2) ,边长为(a-b) 的正方形的面积是(a-b)2 .
所以:(a-b)2=a2-2ab+b2
完全平方公式的特点:(1) 两个公式的等号左边都是一个二项式的完全平方,两者仅有一个“符号”不同;(2) 两个公式的等号右边都是二次三项式,其中首尾两项是等号左边二项式中每一项的平方,中间一项是左边二项式中两项乘积的2倍,两者也仅有一个“符号”不同.
完全平方公式计算的示例:
完全平方公式的常见变形
(1) 完全平方公式中的字母a,b可以是单项式,也可以是多项式,只要符合这个公式的结构特征就可以运用这个公式;(2) 完全平方公式等号右边2ab的符号取决于等号左边二项式中两项的符号,若这两项同号,则2ab的符号为“+”;若这两项异号,则2ab的符号为“-”;(3)运用完全平方公式的时候要避免出现形如(a±b)2 = a2±b2 .
计算下列式子:(1) (4m+n)2 ; (2) (y- )2 .
解: (1) (4m+n)2=(4m)2+2·4m·n+n2=16m2+8mn+n2 ;
解:(1) (-2m-n)2=(2m+n)2=(2m)2+2·2m·n+n2 =4m2+4mn+n2 ;
(2) (2x+3y)(-2x-3y)=-(2x+3y)2=-[(2x)2+2·2x·3y+(3y)2]=-4x2-12xy-9y2 .
计算下列式子:(1) (-2m-n)2 ; (2) (2x+3y)(-2x-3y) .
(3) (-4a+5b)2=(5b-4a)2=(5b)2-2·5b·4a+(4a)2=25b2-40ab+16a2 ;
(4) (x+7y)2 =x2+2·x·7y+(7y)2 =x2+14xy+49y2 .
计算下列式子:(3) (-4a+5b)2 ; (4) (x+7y)2 .
完全平方公式的推导过程
将9.52变形正确的是( )
解析: 9.52=(10-0.5)2=102-2×10×0.5+0.52 .利用完全平方公式即可.
A. 9.52=92+0.52 (10-0.5)(10+0.5)
C. 9.52=102-2×10×0.5+0.52 +9×0.5+0.52
若(3x-a)2=9x2-bx+16,则a+b的值为( ). A.28 B.-28 C.24或-24 D.28或-28
解析:因为(3x-a)2=9x2-6ax+a2,所以9x2-6ax+a2=9x2-bx+16. 则a2=16,6a=b, 解得a=±4. 当a=4时,b=24;当a=-4时,b=-24. 所以a+b=28或-28.
指出下列各式中的错误,并加以改正:(1)(2a - 1)2=2a2 -2a +1 ;(2)(2a + 1)2=4a2 +1 ;(3)(- a - 1)2= - a2 -2a - 1 .
(1)第一数被平方时,未添括号;第一数与第二数乘积的2倍少乘了一个2;应改为: (2a-1)2=(2a)2-2 ×2a •1+1 ;(2)少了第一数与第二数乘积的2倍(丢了一项);应改为: (2a + 1)2=(2a)2 + 2 ×2a •1+1 ; (3)第一数平方未添括号,第一数与第二数乘积的2倍错了符号;第二数的平方这一项错了符号; 应改为: (- a-1)2=(-a)2 - 2 • (- a) •1 +1 2.
初中北师大版6 完全平方公式完美版ppt课件: 这是一份初中北师大版6 完全平方公式完美版ppt课件,共18页。PPT课件主要包含了旧知回顾,你是怎样做的,例2计算,随堂演练等内容,欢迎下载使用。
北师大版七年级下册6 完全平方公式习题ppt课件: 这是一份北师大版七年级下册6 完全平方公式习题ppt课件,共22页。
北师大版七年级下册第一章 整式的乘除6 完全平方公式习题ppt课件: 这是一份北师大版七年级下册第一章 整式的乘除6 完全平方公式习题ppt课件,共18页。













