初中数学北师大版九年级下册1 圆完美版ppt课件

这是一份初中数学北师大版九年级下册1 圆完美版ppt课件，共24页。PPT课件主要包含了学习目标，新课导入，新课讲解，课堂小结，当堂小练，拓展与延伸，布置作业等内容，欢迎下载使用。

1.圆周角的定义2.圆周角和圆心角的关系3.圆周角和弧的关系. （重点、难点）
什么是圆心角？它具有哪些性质？
知识点1 圆周角的定义
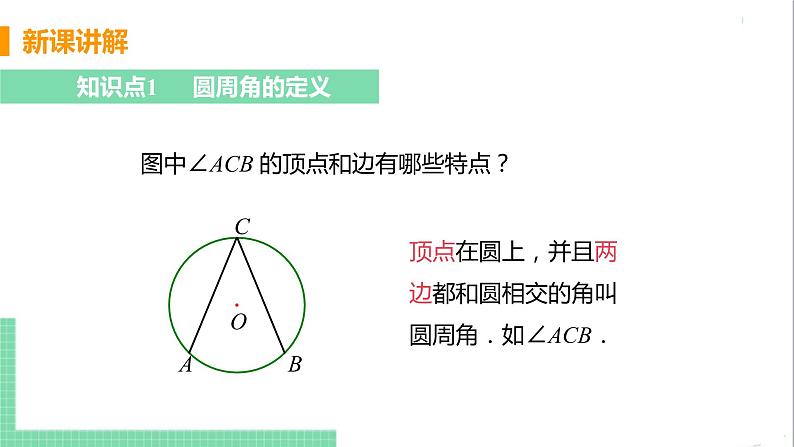
图中∠ACB 的顶点和边有哪些特点？
顶点在圆上，并且两边都和圆相交的角叫圆周角．如∠ACB．
圆周角的特征：①角的顶点在圆上；②角的两边都与圆相交，这两个特征是判定圆周角 不可缺少的条件．
连接OC，如图所示.∵ BC=BD，∴∠ BOC= ∠ BOD=50° .∴∠ A= ∠ BOC= ×50° =25° .
如图所示，AB 是⊙ O 的直径， 弦BC=BD， 若∠BOD=50°，求∠ A 的度数.
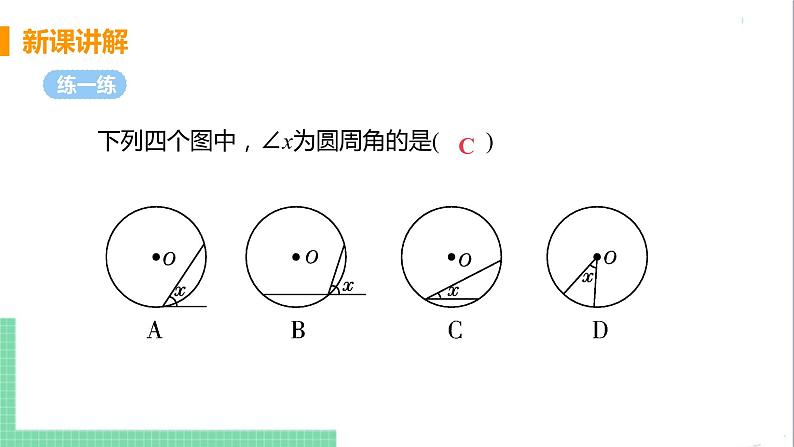
下列四个图中，∠x为圆周角的是(　　)
知识点2 圆周角和圆心角的关系
如图, ∠ AOB = 80°.(1)请你画出几个 所对的圆周角，这几 个圆周角有什么关系？与同伴进行交流.(2 )这些圆周角与圆心角∠ AOB的大小有什 么关系？你是 怎样发现的？与同伴进行交流. 在图中，改变∠ AOB的度数，你得到的结论还成立吗？
圆周角定理：圆周角的度数等于它所对弧上的圆心角度数的一半.
1. 圆周角定理的证明： 已知：如图, ∠ C是 所对的圆 周角， ∠ AOB是 所对的圆心角. 求证： ∠ C= ∠ AOB 分析：根据圆周角和圆心的位置关系，分三种情况讨论：
(1)圆心O在∠ C的一条边上，如图 (1);(2)圆心O在∠ C的内部，如图 (2);(3)圆心O在∠ C的外部，如图 (3). 在三种位置关系中，我们选择(1)给出证明，其他情况可以 转化为(1)的情况进行证明.(1)圆心O在∠ C的一条边上，如图 (1). ∵ ∠ AOB是△AOC的外角，∴ ∠ AOB = ∠ A + ∠ C. ∵ OA = OC，∴ ∠ A = ∠ C. ∴ ∠ AOB = 2 ∠ C, 即 ∠ C = ∠ AOB. 请你完成图 (2)和图 (3)两种情况的证明.
如图，A，B，C，D是同一圆上的点，∠1＝68°，∠A＝40°，则∠D＝________．
由圆周角定理的推论1可知∠C＝∠A＝40°，由三角形的外角性质得∠D＝∠1－∠C＝68°－40°＝28°.
如图，在⊙O中，∠AOC＝150°，求∠ABC，∠ADC的度数，并判断∠ABC和∠ADC，∠EBC和∠ADC之间的度数关系．
解题的关键是分清同弧所对的圆心角和圆周角，如 所对的圆心角是∠AOC，所对的圆周角是∠ABC， 所对的圆心角是大于平角的∠α，所对的圆周角是∠ADC.
∵∠AOC＝150°，∴∠ABC＝ ∠AOC＝75°.∵∠α＝360°－∠AOC＝360°－150°＝210°，∴∠ADC＝ ∠α＝105°.∵∠EBC＝180°－∠ABC＝180°－75°＝105°，∴∠EBC＝∠ADC，即∠EBC与∠ADC相等．又∵∠ABC＋∠ADC＝75°＋105°＝180°，∴∠ABC和∠ADC互补．
如图，在⊙O中，∠O = 50°，求∠A的度数.
解：∵∠BAC与∠BOC 所对的弧都是 ， ∴∠BAC＝ ∠BOC＝ ×50° ＝25°.
知识点3 圆周角和弧的关系
在如图的射门游戏中，当球员在B ， D，E处射门时，所 形成的三个张角∠ ABC， ∠ ADC， ∠ AEC的大小有什么关系？你能用圆周角定理证明你的结论吗？
如图所示，A，P，B，C 是圆上的四个点， ∠ APC=∠ CPB=60°．求证：△ ABC 是等边三角形.
分析：紧扣“同弧所对的圆周角相等”解决.
∵ A，P，B，C 是圆上的四个点，∴∠ ABC= ∠ APC，∠ CPB= ∠ BAC.又∵∠ APC= ∠ CPB=60°，∴∠ ABC= ∠ BAC=60°.∴ AC=BC.又∠ BAC=60°，∴△ ABC 是等边三角形.
如图，哪个角与∠BAC相等？你还能找到哪些相等的角？
解：∠BDC＝∠BAC，如图， 相等的角还有∠ADB＝∠ACB， ∠ACD＝∠ABD， ∠CAD＝∠CBD， ∠1＝∠2，∠3＝∠4.
(1)一个概念（圆周角）；(2)一个定理：一条弧所对的圆周角等于该弧所对的 圆心角的一半；(3)一个推论：同圆内，同弧或等弧所对的圆周角相 等. 相等的圆周角所对的弧相等。
1.将量角器按如图所示的方式放置在三角形纸板上，使顶点C在半圆上，点A，B的读数分别为100°，150°，则∠ACB＝________．
2.如图，在⊙O中，AB＝BC，点D在⊙O上，∠CDB＝25°，则∠AOB＝(　　)A．45° B．50° C．55° D．60°