初中数学19.4 综合与实践 多边形的镶嵌精品同步测试题

19.4综合与实践多边形的镶嵌课时训练

学校:___________姓名：___________班级：___________考号：___________

一、单选题

1．用三块正多边形的木板铺地，拼在一起的三块正多边形木板相交于一点且各边完全吻合，其中两块木板的边数都是5，则第三块木板的边数应是（   ）

A．5 B．6 C．8 D．10

2．用形状、大小完全相同的下列图形，不能进行平面嵌的是（    ）

A．三角形 B．四边形 C．正五边形 D．正六边形

3．如图，下列关于正六边形的说法中，正确的是（    ）

A．内角和为 B．共有六个外角，且外角和为

C．共有条对角线 D．它能与等边三角形进行平面镶嵌

4．下列多边形材料中，不能单独用来铺满地面的是（　　）

A．三角形 B．四边形 C．正五边形 D．正六边形

5．小育到瓷砖店购买一种正多边形瓷砖铺设无缝地板，他购买的瓷砖形状不可以是（    ）

A．正八边形 B．正六边形 C．正方形 D．正三角形

6．下列正多边形地砖中，单独选用一种地砖不能铺满地面的是（    ）

A．正三角形地砖 B．正方形地砖

C．正六边形地砖 D．正八边形地砖

7．如果用边长相同的正三角形和正六边形两种图形铺满平面，那么一个顶点处需要（   ）

A．三个正三角形、两个正六边形 B．四个正三角形、两个正六边形

C．两个正三角形、两个正六边形 D．三个正三角形、一个正六边形

8．某广场准备用边长相等的正方形和正三角形两种地砖铺满地面，在每个顶点的周围，正方形和正三角形地砖的块数分别是（　　）

A．1、2 B．2、1 C．2、2 D．2、3

9．网店出售以下形状的地砖：①正方形；②形状、大小相同的任意四边形；③正五边形；④正六边形、若只购买其中一种地砖镶嵌地面，则不能选择的地砖是（　　）

A．① B．② C．③ D．④

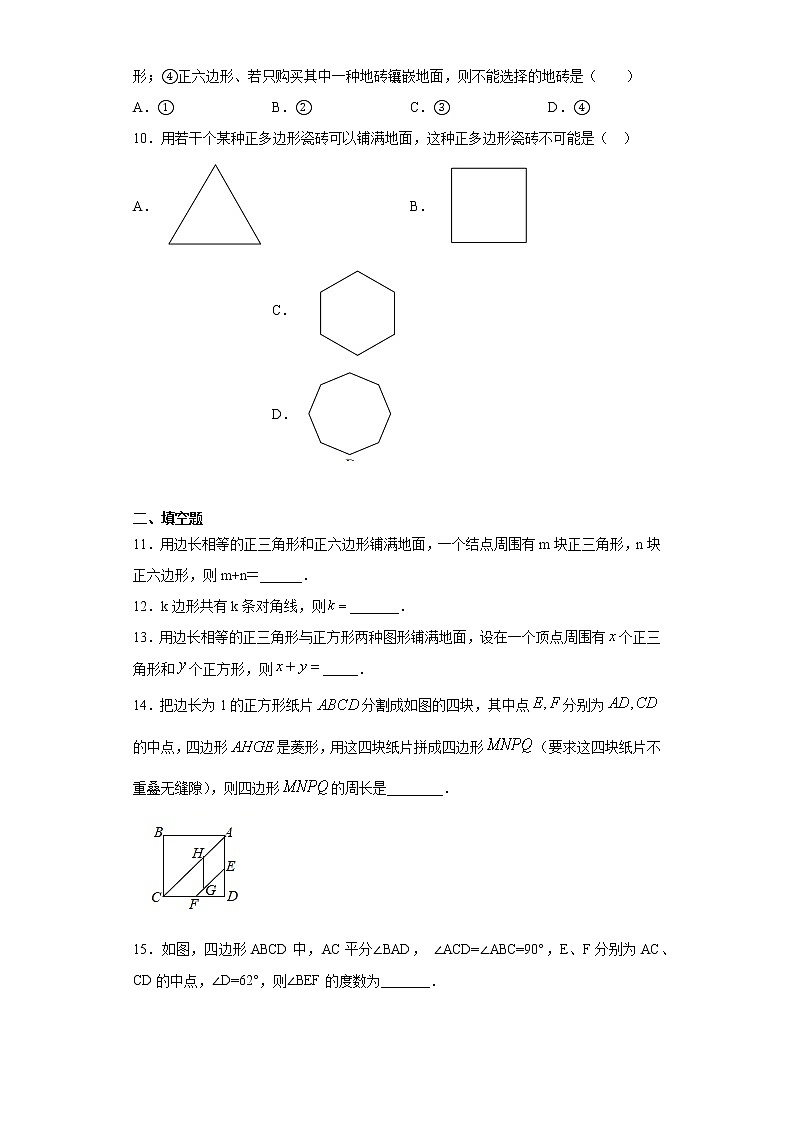
10．用若干个某种正多边形瓷砖可以铺满地面，这种正多边形瓷砖不可能是（  ）

A． B． C． D．

二、填空题

11．用边长相等的正三角形和正六边形铺满地面，一个结点周围有m块正三角形，n块正六边形，则m+n＝______．

12．k边形共有k条对角线，则_______．

13．用边长相等的正三角形与正方形两种图形铺满地面，设在一个顶点周围有个正三角形和个正方形，则_____．

14．把边长为1的正方形纸片分割成如图的四块，其中点分别为的中点，四边形是菱形，用这四块纸片拼成四边形（要求这四块纸片不重叠无缝隙），则四边形的周长是________．

15．如图，四边形ABCD中，AC平分∠BAD， ∠ACD=∠ABC=90°，E、F分别为AC、CD的中点，∠D=62°，则∠BEF的度数为_______．

16．使用下列同一种正多边形不能铺满地面的是________（填序号）

①正三角形；    ②正方形；    ③正六边形；    ④正八边形

三、解答题

17．已知个正多边形和个正多边形可绕一点周围镶嵌（密铺），的一个内角的度数是的一个内角的度数的．

（1）试分别确定，是什么正多边形？

（2）画出这个正多边形在平面镶嵌（密铺）的图形（画一种即可）．

18．用边长相等的正方形和正三角形镶嵌平面．

（1）则一个顶点处需要几个正方形、几个正三角形？（两种图形都要用上）

（2）请画出你的镶嵌图．

19．[动手操作] 如图所示，地面全是用正三角形的材料铺设而成的．

(1)用这种形状的材料为什么能铺成平整、无缝隙的地面？

(2)像上面那样铺地砖，能否全用正十边形的材料？为什么？

(3)你能不能另外想出用一种相同的正多边形材料铺地面的方案？并画出草图．

参考答案

1．D

2．C

3．D

4．C

5．A

6．D

7．C

8．D

9．C

10．D

11．4或5

12．5

13．5

14．或或4

15．84°

16．④

17．（1）A为正四边形，B为正三边形；（2）见解析

解：（1）设B的内角为x，则A的内角为x，

∵2个正多边形A和3个正多边形B可绕一点周围镶嵌（密铺），

∴3x+2×x=360°，

解得：x=60°，

∴x=90°
∴可确定A为正四边形，B为正三边形．
（2）所画图形如下：
 

18．（1）3个正三角形和2个正方形可作平面镶嵌；（2）如图所示见解析.

解：（1）正三角形的一个内角度数为180﹣360÷3=60°，正方形的一个内角度数为180﹣360÷4=90°，因为3×60+2×90=360°，那么3个正三角形和2个正方形可作平面镶嵌；

（2）如图所示：

．

19．(1)见解析;(2)见解析;(3)见解析.

解：(1)因为正三角形的每个内角都是60°，而图中每个顶点处都有6个正三角形的内角，它们恰好组成一个周角，所以能铺成平整、无缝隙的地面．

(2)不能．理由：因为正十边形的每个内角都是144°，图中每个顶点处的几个内角不能组成周角，所以不能全用正十边形的材料．

(3)如图所示：