数学九年级下册3 三角函数的计算评优课ppt课件

这是一份数学九年级下册3 三角函数的计算评优课ppt课件，共24页。PPT课件主要包含了y-3x2-2，yax2+c，yax2，开口方向，a0时向上，a0时向下，对称轴，顶点坐标，上正下负，完成下表等内容，欢迎下载使用。

1.函数 的图象的顶点坐标是 ；开口方向是 ；最 值是 .2.函数y=-2x2+3的图象可由函数y=-2x2的图象向 平移 个单位得到.3.把函数y=-3x2的图象向下平移2个单位可得到函数__________的图象.
二次函数y=ax2与y=ax2+c的图象有什么关系？
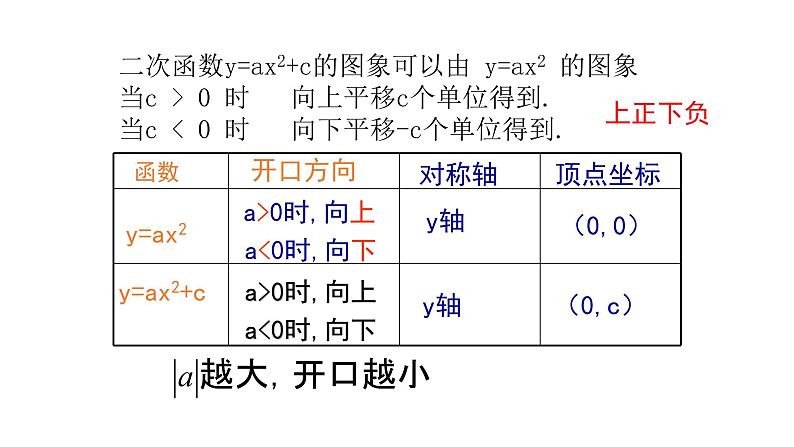
二次函数y=ax2+c的图象可以由 y=ax2 的图象当c > 0 时 向上平移c个单位得到.当c < 0 时 向下平移-c个单位得到.
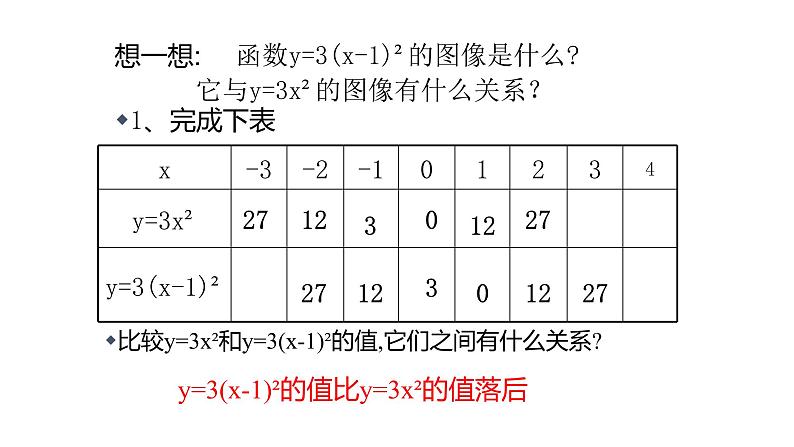
函数y=3(x-1)²的图像是什么?它与y=3x²的图像有什么关系？
比较y=3x²和y=3(x-1)²的值,它们之间有什么关系?
y=3(x-1)²的值比y=3x²的值落后
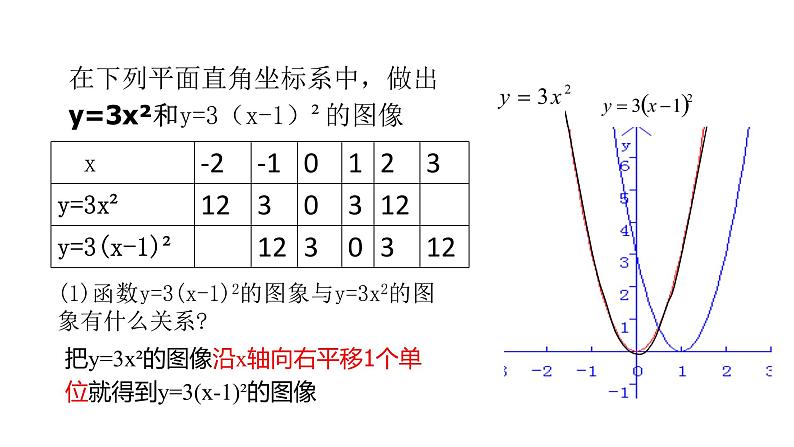
在下列平面直角坐标系中，做出y=3x²和y=3（x-1）²的图像
(1)函数y=3(x-1)2的图象与y=3x2的图象有什么关系?
把y=3x²的图像沿x轴向右平移1个单位就得到y=3(x-1)²的图像
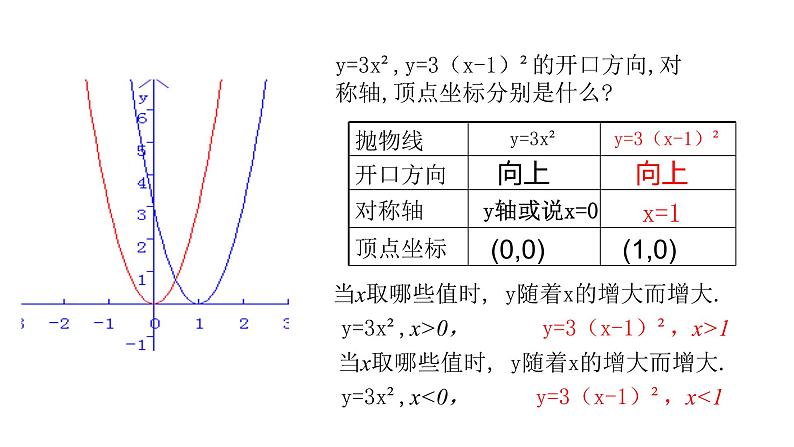
y=3x²,y=3（x-1）²的开口方向,对称轴,顶点坐标分别是什么?
当x取哪些值时, y随着x的增大而增大.
y=3（x-1）²，x>1
y=3（x-1）²，x<1
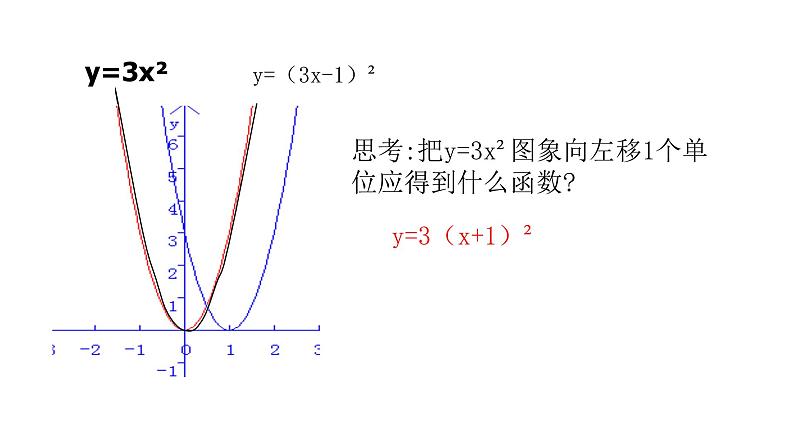
思考:把y=3x²图象向左移1个单位应得到什么函数?
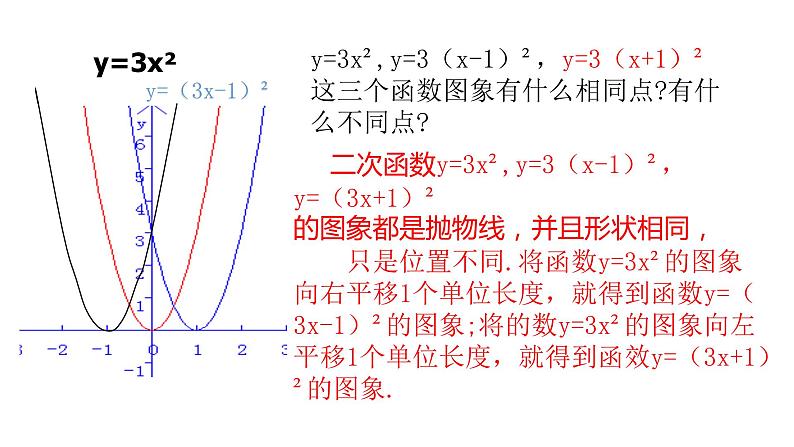
y=3x²,y=3（x-1）²，y=3（x+1）²这三个函数图象有什么相同点?有什么不同点?
二次函数y=3x²,y=3（x-1）²，y=（3x+1）²的图象都是抛物线，并且形状相同， 只是位置不同.将函数y=3x²的图象向右平移1个单位长度，就得到函数y=（3x-1）²的图象;将的数y=3x²的图象向左平移1个单位长度，就得到函效y=（3x+1）²的图象.
将函数 y=2x²的图象向右平移1个单位, 就得到 y=2(x-1)²的图象; 在向左平移2个单位,得到函数 y=2(x+1)²的图象.相同点: (1)图像都是抛物线,形状、大小相同,开口方向相同. (2)都是轴对称图形. (3)顶点都是最低点. (4) 在对称轴左侧,都随 x 的增大而减小,在对称轴 右侧,都随 x 的增大而增大. (5)它们的增长速度相同.不同点: (1)对称轴不同. (2)顶点不同.
比较y=2x²， y=2(x-1)²,y=2(x+1)²的图象;
可得到函数y=a（x-h）2的图象
对称轴是直线x=h ；
函数y=ax2的图象向右平移h（h﹥0）个单位(向左平移︱h︱（h﹤0）个单位)
函数y=a（x-h）2的图象：
函数y=ax2与y=a(x-h)2的图象关系：
1.抛物线y=3x2－4与抛物线y =3x2 的_______相同，_________不同.2.抛物线y =3(x－1)2与抛物线y =3x2 的______相同，_________不同.3.抛物线y =3x2+5的开口_______，对称轴是______，顶点坐标是____________.4.抛物线y =－2(x+1)2的开口__________，对称轴是___________，顶点坐标是_____________.
5.将抛物线y=-x2向左平移2个单位后，得到的抛物线的解析式是（ ）.
1、画出二次函数y=3（x-1）2+2的图象，2、并与二次函数y=3x2的图象进行比较，说明它们之间的关系.
函数y=3x2 的图象
函数y=3x2+2 的图象
函数y=3(x-1)2 的图象
函数y=3(x-1)2 +2的图象
再看下课本上的：在同一坐标系中作出二次函数y=2x²-1/2, y=2(x+3)2和y=2(x+3)2-1/2的图象.
二次函数y=2x²-1/2 , y=2(x+3)2和y=2(x+3)2-1/2的图象有什么关系?它们的开口方向,对称轴和顶点坐标分别是什么?
y=2(x+3)2 -1/2
练一练： 由二次函数y=3x²的图象,你能得到二次函数y=3x²+2，y=3（x-1）²，y=3（x-2）²-5的图象吗？
y=（3x-1）²的图象
y=3x²向右移平移2个单位，再向下平移5个单位可得y=3（x-2）²-5的图象
y=3x²向下平移5个单位再向右移平移2个单位，可得y=3（x-2）²-5的图象
（当k,h都大于0时）的图象特点
y=a(x-h)2的图象
y=a(x-h)2+k的图象
y=a(x-h)2+k的图象一条抛物线，
a>0开口向上，a<0开口向下
议一议：二次函数y=a(x-h)2+k 的图象与y=ax2 有什么关系？
y=ax2+bx+c的二次函数平移时,a的大小不会变
y=2(x+1)2+2
y=-(x-1)2+2
y=a(x-h)2+k(a<0)
1.y=a(x-h)2+k的图象的特征.
2.y=a(x-h)2+k的图象与y=ax2的图象的关系.
　　 抛物线 　　　　　　 有如下特点：　　（1）当 a＞0 时，开口向上；当 a＜0 时，开口向下．　　（2）对称轴为直线 x = h．　　（3）顶点坐标（h，k）．　　（4）如果 a＞0，当 x＜h 时，y 随 x 的增大而减小，当 x＞h 时，y 随 x 的增大而增大； 如果 a＜0，当 x＜h 时，y 随 x 的增大而增大，当 x＞h 时，y 随 x 的增大而减小． （5）当 a＞0 时，y 有最小值k（即y ≥k）；当 a＜0 时，y 有最大值k（即y ≤k）
y = a（x - h）2 + k
1. 已知二次函数y=-（x-4）2+4.（1）写出其图象的开口方向，对称轴和顶点坐标；（2）x取何值时，①y=0，②y＞0，③y＜0.
解：（1）∵二次函数y=-（x-4）2+4中，a=-1＜0，∴抛物线开口向下，对称轴为直线x=4，顶点坐标为（4，4）. （2）当y=0时，-（x-4）2+4=0，解得x=2或x=6.①x=2或x=6时，y=0；②2＜x＜6时，y＞0；③x＜2或x＞6时，y＜0.
2.如图X2-2-6，抛物线y=2(x-2)2-6的顶点为C，且一次函数y=-kx＋3的图象经过点C，求这个一次函数的图象与两坐标轴所围成的三角形的面积．
解：根据题意，得点C的坐标为(2，-6),由y=-kx＋3的图象经过点C，得-6=-2k＋3，解得k= ，∴y=- x＋3.从而得此一次函数图象与两坐标轴的交点坐标分别为 ，(0，3)，∴一次函数图象与两坐标轴所围成三角形的面积为 ×3=1.