初中数学人教版八年级下册18.1.1 平行四边形的性质优秀ppt课件

这是一份初中数学人教版八年级下册18.1.1 平行四边形的性质优秀ppt课件，共20页。PPT课件主要包含了情境引入，对边平行，平行四边形的定义，特别说明，两组对边不平行，记作ABCD，记法与读法，相关元素，边和角，探究方法等内容，欢迎下载使用。

1.理解并掌握平行四边形的概念及其性质.（重点）2.根据平行四边形的性质进行简单的计算和证明.（难点）
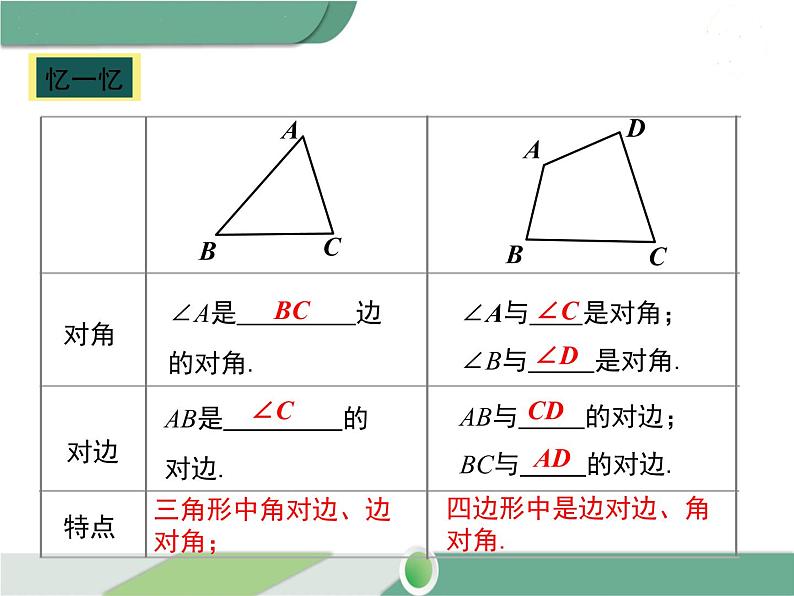
∠A是 边的对角.
∠A与 是对角；∠B与 是对角.
AB是 的对边.
AB与 的对边；BC与 的对边.
三角形中角对边、边对角；
四边形中是边对边、角对角.
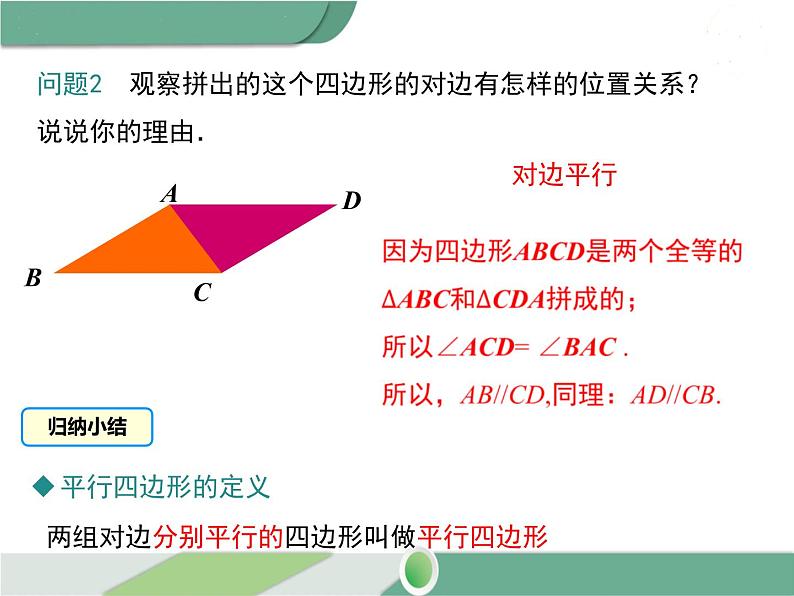
问题1 用两个全等的三角形，能拼出怎样的四边形？ 拼拼看.
问题2 观察拼出的这个四边形的对边有怎样的位置关系？说说你的理由．
两组对边分别平行的四边形叫做平行四边形
问题3 黑板上展示的图形中，还有哪些是平行四边呢？为什么？
定义可以用来判别一个四边形是否是平行四边形
问题4 黑板上展示的图形(如下图）中，另外三个是不是平行四边呢？为什么不是？
这两个四边形不属于初中的学习范围
这种两组邻边分别相等的四边形叫做“筝形”
问题5 只有一组对边平行的四边形是不是平行四边形呢？是什么特殊四边形？
不是平行四边形，是梯形.
读作： 平行四边形ABCD
对角：∠A与∠C， ∠B与∠D.
对边：AB 与CD， AD与BC.
对角线：AC、BD.
问题6 研究等腰三角形的性质是从哪些方面考虑的？
1.小组合作：同学们利用学具（全等的三角形纸板）．
2.汇报结论：学生展示实验过程，相互补充探究出的结论．
3.说理验证：请大家思考一下，利用我们以前学习的几何知识通过说理能验证这三个结论吗？
那么研究平行四边形首先可以从哪些方面考虑？
由上面知，△ABC≌△CDA ∴ ∠1=∠2，∠3=∠4∴∠1+∠4=∠2+∠3即∠BAD=∠DCB.
证明：如图，连接AC∵AD∥BC，AB ∥ CD∴∠1=∠2，∠3=∠4又AC是△ABC和△CDA的公共边，∴ △ABC≌ △CDA∴AD=CD，AB=CD，∠B=∠D
1.同学们自己证明∠BAD=∠DCB
2.不添加辅助线，你能否直接运用平行四边形的定义，证明其对角相等？
∵ 四边形ABCD是平行四边形，
∴ AD∥BC ，AB∥DC.
∴ AD=BC ，AB=DC.
∴ ∠A=∠C，∠ B=∠D.
例1 如图，在□ABCD中
(1)若∠A=130°，则∠B=______ ，∠C=______ ， ∠D=______。
(2)若∠A+ ∠C= 200°，则∠A=______ ，∠B=______.
(3)若∠A:∠B= 5:4，则∠C=______ ，∠D=______.（4）若AB=3,BC=5,则它的周长= ______.
（1）平行四边形的对角相等；（2）平行四边形的 邻角互补；（3）平行四边形的一组邻边之和等于周长的一半,反之，周长=2倍邻边之和.
若a // b，作 AD // GH // BC，分别交 b于D、H、C，交 a于A、G、B.
则 GH=AD=BC.
两条平行线之间的平行线段相等
则 DA HG CB.
（因为平行四边形的对边相等）
若a // b，DA、GH、CB垂直于 a，交a于A、G、B，交 b于D、H、C.
1.在□ABCD中，M是BC延长线上的一点，若∠A=135°，则∠MCD的度数是（ ） A .45° B. 55° C. 65° D. 75°
2.在□ABCD中，AD=8,AE平分∠BAD交BC于点E,DF平分∠ADC交BC于点F,且EF=2,则AB的长为（ ） A .3 B. 5 C. 2或3 D. 3或5
3.在□ABCD中, ∠A: ∠B: ∠C=1:2:1,则∠D等于 .
4.如图，直线AE//BD，点C在BD上，若AE=5，BD=8，△ABD的面积为16，则△ACE的面积为 .
5.有一块形状如图 所示的玻璃，不小心把EDF部分打碎了，现在只测得AE=60cm，BC=80cm，∠B=60°且AE∥BC、AB∥CF,你能根据测得的数据计算出DE的长度和∠D的度数吗？
解：∵AE//BC，AB//CF，
∴四边形ABCD是平行四边形.
∴∠D=∠B=60°，AD=BC=60cm.
∴ED=AD-AE=80-60=20cm.
答：DE的长度是20cm, ∠D的度数是60°.