初中数学4 平行线的性质评优课课件ppt

这是一份初中数学4 平行线的性质评优课课件ppt，共22页。PPT课件主要包含了两直线平行，同位角相等，内错角相等，同旁内角互补，平行线的性质，今天的收获，今天的作业等内容，欢迎下载使用。

学习目标：1、掌握平行线的性质定理，能运用平行线的性质定理。2、了解平行线的性质定理与平行线的判断定理的联系。3、进一步理解证明的步骤、格式和和方法，发展学生的推理能力。
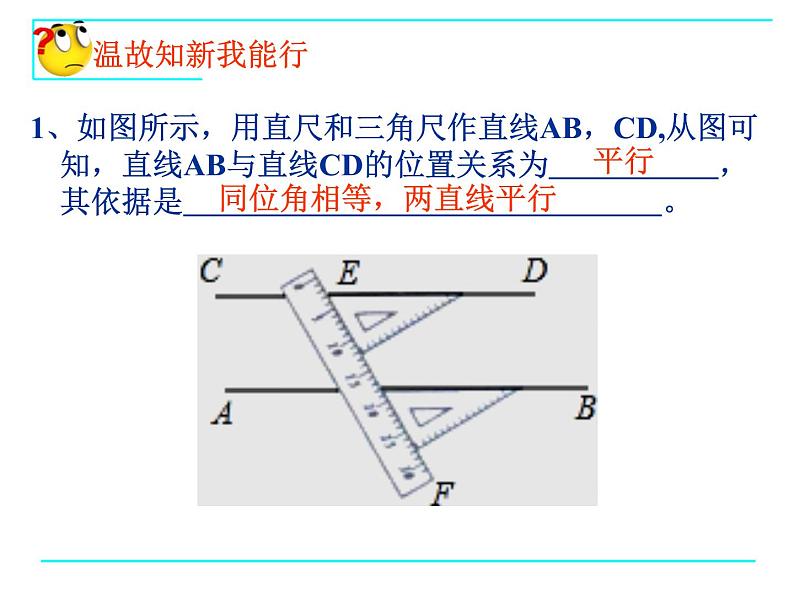
1、如图所示，用直尺和三角尺作直线AB，CD,从图可知，直线AB与直线CD的位置关系为 ，其依据是 。
同位角相等，两直线平行
内错角相等，两直线平行
同旁内角互补，两直线平行
平行于同一条直线的两条直线互相平行
2、完成下列推理，并在括号中写出相应的根据.
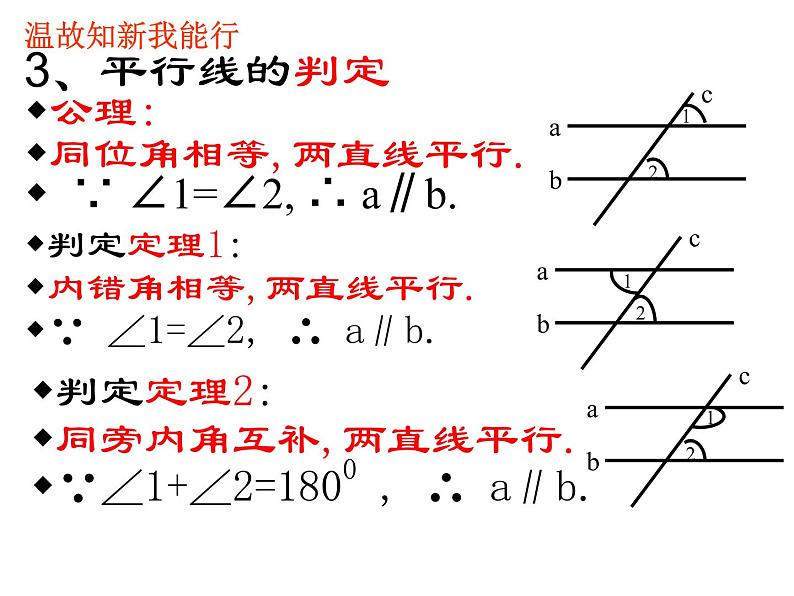
公理:同位角相等,两直线平行. ∵ ∠1=∠2, ∴ a∥b.
判定定理1:内错角相等,两直线平行.∵ ∠1=∠2, ∴ a∥b.
判定定理2:同旁内角互补,两直线平行.∵∠1+∠2=1800 , ∴ a∥b.
4、如果我们把平行线的判定定理的条件和结论互换会怎么样呢?
两直线平行，同位角相等。
两直线平行，内错角相等。两直线平行，同旁内角互补。
这三个命题都是真命题吗？
1、证明：两条平行线被第三条直线所截， 同位角相等。
已知：直线AB∥CD,∠1和∠2是直线AB，CD被直线EF截出的同位角。 求证： ∠1=∠2
证明：假设∠1≠∠2，那么可以过点M作直线GH，使∠EMH=∠2， ∴GH∥CD ∵AB∥CD ∴过点M有两条直线AB和GH与直线CD平行 ∴这与基本事实“过直线外一点有且只有一条直线与这条直线平行”相矛盾 ∴ ∠1≠∠2不成立 ∴∠1=∠2
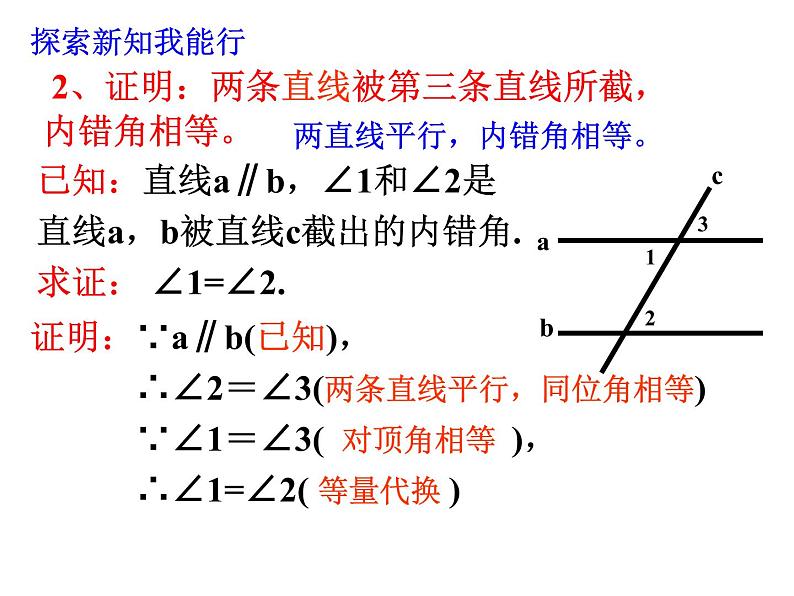
2、证明：两条直线被第三条直线所截，内错角相等。
已知：直线a∥b，∠1和∠2是直线a，b被直线c截出的内错角.求证： ∠1=∠2.
证明：∵a∥b(已知)， ∴∠2＝∠3(两条直线平行，同位角相等) ∵∠1＝∠3( 对顶角相等 )， ∴∠1=∠2( 等量代换 )
两直线平行，内错角相等。
3、 证明：两条直线被第三条直线所截，同旁内角互补。
已知：直线a∥b，∠1和∠2是直线a，b被直线c截出的同旁内角.求证： ∠1+∠2=180°.
证明：∵a∥b (已知) ∴∠2＝∠3 (两条直线平行，同位角相等) ∵∠1+∠3 =180°（平角的定义 ） ∴∠1+∠2=180 ° (等量代换)
两直线平行，同旁内角互补。
平行线的判定与性质的关系：
两直线平行，同位角相等。两直线平行，内错角相等。两直线平行，同旁内角互补。
1、已知平行线AB、CD被直线AE所截
从∠1＝110°，可以知道∠2是（ ）度，根据（ ）
从∠1=110°，可以知道∠3是（ ）度，根据（ ）
从∠1=110°，可以知道∠4是（ ）度， 根据（ ）
2、如图是梯形有上底的一部分，量得∠A=115°，∠D＝100°，则∠B= ,∠C= 。
3、如图，AC∥DF，AB∥EF，点D，E分别在AB，AC上，∠2=50°，则∠1的大小是（ ）。
4、如图所示，AB∥CD，若∠2是∠1的2倍，则∠1=（ ）。
5、已知：如图，AD∥BC，∠ABD=∠D．求证：BD平分∠ABC．
证明：∵AD∥BC，∴∠D=∠CBD，∵∠ABD=∠D，∴∠ABD=∠CBD，∴BD平分∠ABC
1、如图，一块直角三角板的两个顶点分别在直尺的对边上．若∠1=30°，那么∠2= 度．
2、如图，在甲，乙两地之间修一条笔直公路，从甲地测得公路的走向是北偏东50°，甲，乙两地同时开工，若干天后，公路准确接通，则乙地所修公路走向是（　　） A．北偏45° B．南北方向 C．南偏西50° D．以上都不对
3、如图，已知CD∥AB，∠DCB=70°，∠CBF=20°，∠EFB=130°，求证：AB∥EF．
证明：∵CD∥AB，∠DCB=70°，∴∠DCB=∠CBA=70°．∵∠CBA=∠ABF+∠CBF，∠CBF=20°，∴∠ABF=50°．∵∠EFB=130°，∴∠EFB+∠ABF=180°，∴AB∥EF．
4、如图，已知CD∥AB，∠DCB=70°， AB∥EF ，∠EFB=130°，求 ∠CBF的度数 ．
1、如图，AB∥ED，AG平分∠BAC，∠ECF=70°，则∠FAG的度数是（ 　　）
2、如图，已知AB∥EG，BC∥DE，∠B=40°，则∠E=( )
3、如图，已知B，E分别是AC，DF上一点，∠1=∠2，∠C=∠D。求证：∠A=∠F。
证明：∵∠1=∠2，∠2=∠3， ∴∠1=∠3， ∴BD∥CE， ∴∠C=∠DBA， ∵∠C=∠D， ∴∠D=∠DBA， ∴DF∥AC， ∴∠A=∠F．
1、如图，已知∠BAP与∠APD互补，∠1=∠2，求证∠E=∠F．
2、如图，已知AB∥CD，CE、AE分别平分∠ACD、∠CAB，求证：AE⊥CE。