


人教版九年级下册27.2.3 相似三角形应用举例精品课件ppt
展开利用影子测量物体的高度
借助标杆测量物体的高度
利用平面镜的反射测量物体的高度
1.能够利用相似三角形的知识,求出不能直接测量的物体的宽度.
2.进一步了解数学建模思想,能够将实际问题转化为相似三角形的数学模型,提高分析问题、解决问题的能力.
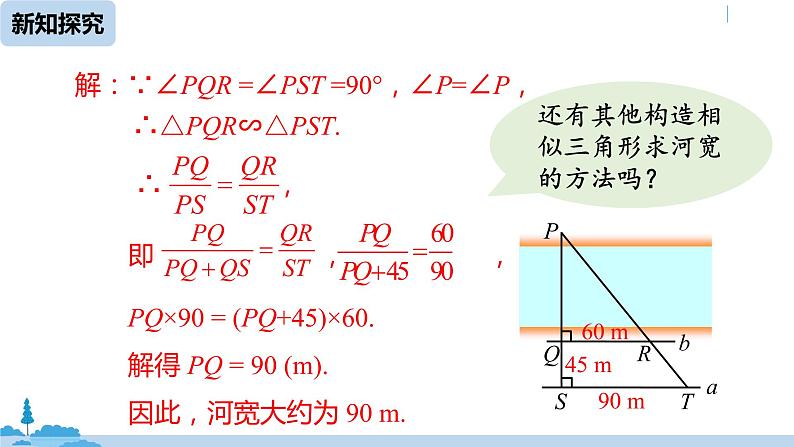
例5 如图,为了估算河的宽度,我们可以在河对岸选定一个目标点 P,在近岸取点 Q 和 S,使点 P,Q,S共线且直线 PS 与河垂直,接着在过点 S 且与 PS 垂直的直线 a 上选择适当的点 T,确定 PT 与过点 Q 且垂直 PS 的直线 b 的交点 R. 已测得QS = 45 m,ST = 90 m,QR= 60 m,请根据这些数据,计算河宽 PQ.
PQ×90 = (PQ+45)×60.解得 PQ = 90 (m).因此,河宽大约为 90 m.
解:∵∠PQR =∠PST =90°,∠P=∠P,
∴△PQR∽△PST.
还有其他构造相似三角形求河宽的方法吗?
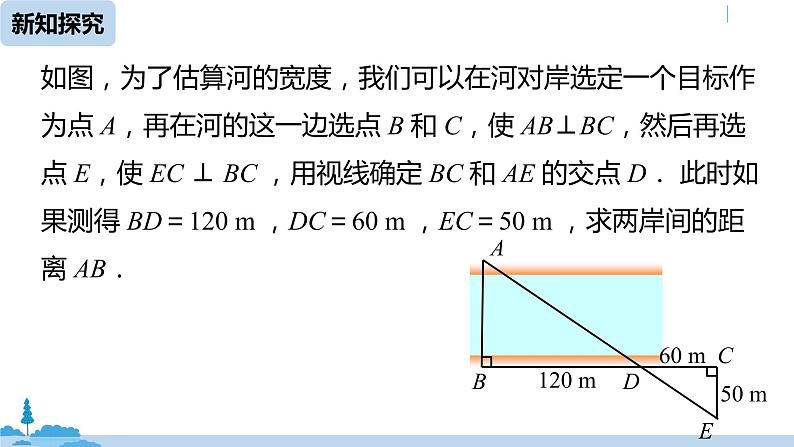
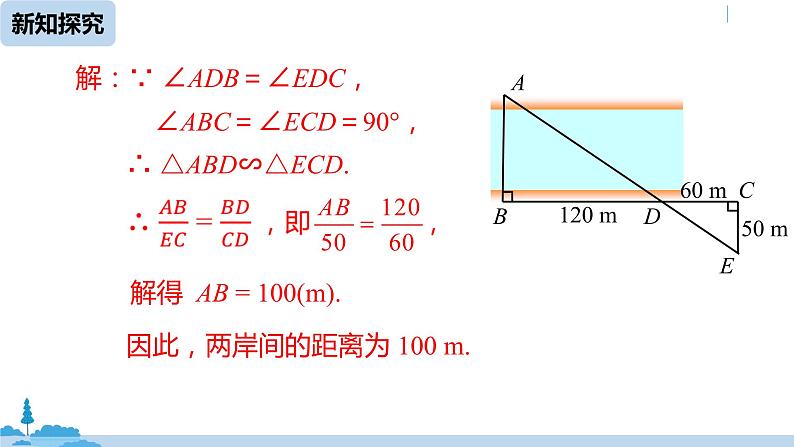
如图,为了估算河的宽度,我们可以在河对岸选定一个目标作为点 A,再在河的这一边选点 B 和 C,使 AB⊥BC,然后再选点 E,使 EC ⊥ BC ,用视线确定 BC 和 AE 的交点 D. 此时如果测得 BD=120 m ,DC=60 m ,EC=50 m ,求两岸间的距离 AB.
解:∵ ∠ADB=∠EDC,
∠ABC=∠ECD=90°,
∴ △ABD∽△ECD.
解得 AB = 100(m).
因此,两岸间的距离为 100 m.
测量不能直接到达的两点间的距离,常常构造“X”型或“A”型相似三角形,利用相似三角形的性质计算两点间的距离.
1.如图,M,N 为山两侧的两个村庄,为了两村交通方便,根据国家的惠民政策,政府决定打一直线涵洞,工程人员为计算工程量,必须计算 M,N 两点之间的距离,选择测量点 A,B,C,点 B,C 分别在 AM,AN 上,现测得AM = 1000 米,AN = 1800 米,AB = 54米,BC = 45米,AC = 30 米,求 M,N 两点之间的距离.
2.如图,为了测量水塘边 A、B 两点之间的距离,在可以看到 A、B 的点 E 处,取 AE、BE 延长线上的 C、D 两点,使得 CD//AB. 若测得 CD=5 m,AD=15m,ED=3 m,则 A、B 两点间的距离为 m.
2.如图,一只箱子沿着斜面向上运动,箱高 AB = 1.3 m,当 BC = 2.6 m时,点 B 离地面的距离 BE =1 m,则此时点 A 离地面的距离是( )A. 2.2 mB. 2 mC. 1.8 mD. 1.6 m
3.某高中学校为高一新生设计的学生板凳从正面看到的平面图形如图所示,其中 BA =CD,BC = 20 cm,BC 与 EF 平行于 AD,且到 AD 的距离分别为 40 cm,8 cm.为使板凳两腿底端 A,D 之间的距离为 30 cm,那么横梁 EF 应为多长?(材质及其厚度等忽略不计)
解:如图,过点 C 作 CM //AB,分别交 EF,AD 于点 N,M.作 CP⊥AD,分别交 EF,AD 于点 Q,P.∵ BC//AD,EN//AD,∴四边形 ABCM 和四边形 AENM 均是平行四边形,∴EN =AM =BC = 20 cm,∴ MD =AD -AM =30-20=10(cm).由题意知 CP =40 cm,PQ =8 cm,∴ CQ =CP - PQ =32 cm.
1.(2020·玉林中考)一个三角形木架三边长分别是 75 cm,100 cm,120 cm,现要再做一个与其相似的三角形木架,而只有长为 60 cm 和 120 cm 的两根木条.要求以其中一根为一边,从另一根截下两段作为另两边(允许有余料),则不同的截法有( )A.一种B.两种C.三种D.四种
2.(2020·上海中考)《九章算术》中记载了一种测量井深的方法.如图所示,在井口 B 处立一根垂直于井口的木杆 BD,从木杆的顶端 D 观察井水水岸 C,视线 DC 与井口的直径 AB 交于点 E,如果测得 AB =1.6米,BD =1米,BE =0.2米,那么井深 AC 为 米.
3.(2018·陕西中考)周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸岸边的一棵大树,将其底部作为点 A,在他们所在的岸边选择了点 B,使得 AB 与河岸垂直,并在 B 点竖起标杆 BC,再在 AB 的延长线上选择点 D,竖起标杆 DE,使得点 E 与点 C、A 共线.已知:CB⊥AD,ED⊥AD,测得 BC =1 m,DE =1.5 m,BD =8.5 m.测量示意图如图所示.请根据相关测量信息,求河宽 AB.
数学九年级下册27.2.3 相似三角形应用举例课文内容课件ppt: 这是一份数学九年级下册27.2.3 相似三角形应用举例课文内容课件ppt,共19页。
人教版九年级下册27.2.3 相似三角形应用举例示范课课件ppt: 这是一份人教版九年级下册27.2.3 相似三角形应用举例示范课课件ppt,共30页。PPT课件主要包含了乐山大佛,图片引入,怎样测量河宽,怎样测出OA的长,测高方法一,练一练,△ABO∽△AEF,平面镜,想一想,测高方法二等内容,欢迎下载使用。
初中数学人教版九年级下册27.2.3 相似三角形应用举例教课课件ppt: 这是一份初中数学人教版九年级下册27.2.3 相似三角形应用举例教课课件ppt,文件包含2723相似三角形应用举例pptx、2723相似三角形应用举例docx等2份课件配套教学资源,其中PPT共30页, 欢迎下载使用。














