



2021版《5年中考3年模拟》全国版中考数学:§7.2 概 率
展开1.(2020湖北武汉,3,3分)两个不透明的口袋中各有三个相同的小球,将每个口袋中的小球分别标号为1,2, 3.从这两个口袋中分别摸出一个小球,则下列事件为随机事件的是 ( )A.两个小球的标号之和等于1 B.两个小球的标号之和等于6C.两个小球的标号之和大于1 D.两个小球的标号之和大于6
答案 B ∵两个小球的标号之和可取2,3,4,5,6,∴选项A是不可能事件,选项B是随机事件,选项C是必然 事件,选项D是不可能事件.
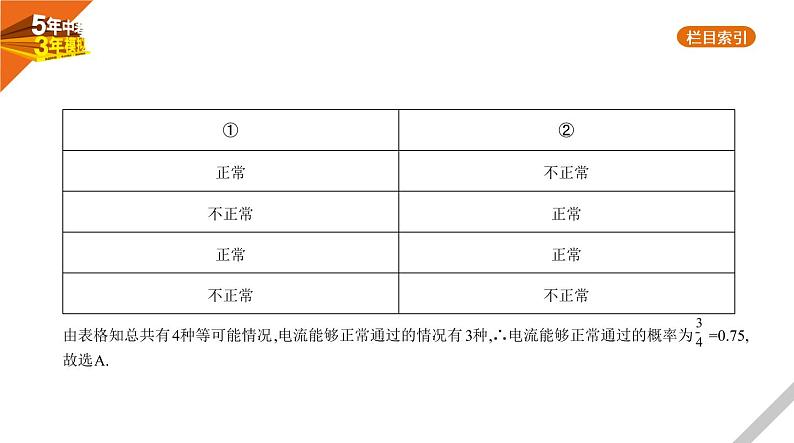
2.(2020内蒙古呼和浩特,4,3分)已知电流在一定时间段内正常通过电子元件“ ”的概率是0.5,则在一定时间段内,由该元件组成的图示电路A,B之间,电流能够正常通过的概率是 ( ) C.0.5
答案 A 设电路中两条支路分别为①,②,则电流通过电子元件可用表格表示为:
由表格知总共有4种等可能情况,电流能够正常通过的情况有3种,∴电流能够正常通过的概率为 =0.75,故选A.
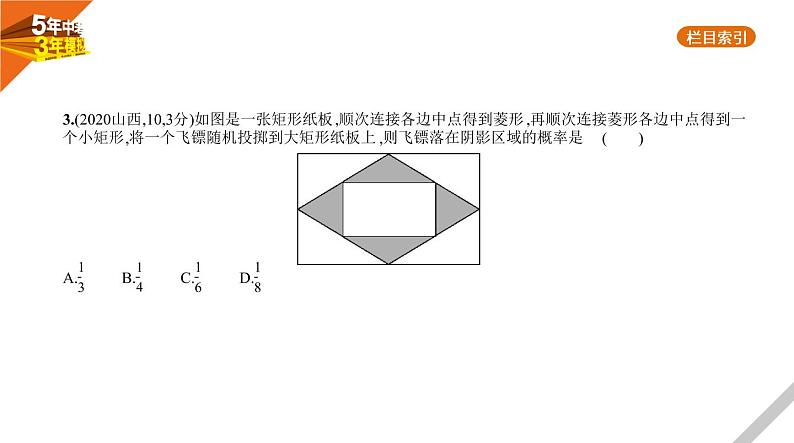
3.(2020山西,10,3分)如图是一张矩形纸板,顺次连接各边中点得到菱形,再顺次连接菱形各边中点得到一 个小矩形,将一个飞镖随机投掷到大矩形纸板上,则飞镖落在阴影区域的概率是 ( ) A. B. C. D.
答案 B 设矩形纸板的长和宽分别为a,b,则矩形纸板的面积为ab,菱形的面积为ab-4× × × = ab,由已知易求小矩形的长和宽分别为 , ,则小矩形的面积为 × = ab,∴阴影区域的面积为 ab- ab= ab,∴飞镖落在阴影区域的概率为 = ,故选B.
4.(2019黑龙江齐齐哈尔,9,3分)在一个不透明的口袋中,装有一些除颜色外完全相同的红、白、黑三种 颜色的小球.已知袋中有红球5个,白球23个,且从袋中随机摸出一个红球的概率是 ,则袋中黑球的个数为 ( )A.27 B.23 C.22 D.18
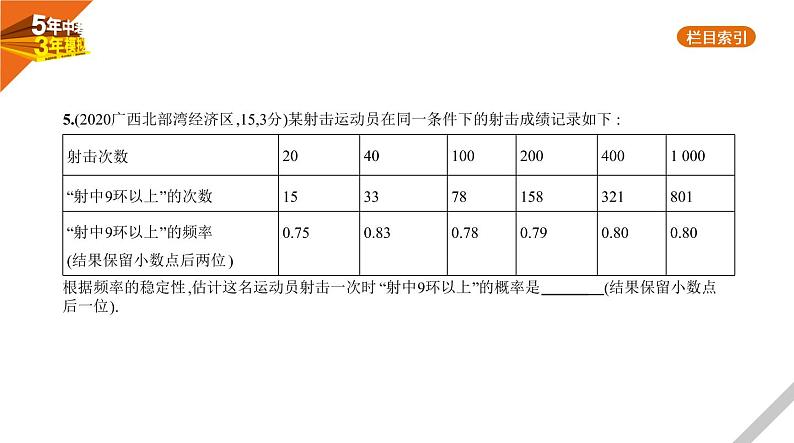
5.(2020广西北部湾经济区,15,3分)某射击运动员在同一条件下的射击成绩记录如下:
根据频率的稳定性,估计这名运动员射击一次时“射中9环以上”的概率是 (结果保留小数点 后一位).
解析 从题表中的数据可知,随着射击次数的逐步增加,“射中9环以上”的频率稳定在0.80,所以估计这 名运动员射击一次时“射中9环以上”的概率为0.8.
6.(2020内蒙古呼和浩特,14,3分)公司以3元/kg的成本价购进10 000 kg柑橘,并希望出售这些柑橘能够获 得 12 000 元利润.在出售柑橘(去掉损坏的柑橘)时,需要先进行“柑橘损坏率”统计,再大约确定每千克 柑橘的售价.下面是销售部通过随机取样,得到的“柑橘损坏率”统计表的一部分,由此可估计柑橘完好 的概率为 (精确到0.1);从而可大约确定每千克柑橘的实际售价为 元时(精确到0.1),可 获得12 000 元利润.
解析 随着试验次数的增多,柑橘损坏的频率越来越稳定在0.1左右,利用频率估计概率可估计柑橘完好 的概率大约是0.9.设每千克柑橘的实际售价为x元,依题意得10 000×0.9·x-3×10 000=12 000.解得x≈4.7.
考点二 用列举法求概率
1.(2020宁夏,3,3分)现有4条线段,长度依次是2、4、6、7,从中任选三条,能组成三角形的概率是 ( )A. B. C. D.
2.(2020广西北部湾经济区,8,3分)一只蚂蚁在如图所示的树枝上寻觅食物,假定蚂蚁在每个岔路口都随 机选择一条路径,则它获得食物的概率是 ( )A. B. C. D.
3.(2020湖北武汉,6,3分)某班从甲、乙、丙、丁四位选手中随机选取两人参加校乒乓球比赛,恰好选中 甲、乙两位选手的概率是 ( )A. B. C. D.
4.(2019内蒙古呼和浩特,13,3分)同时掷两枚质地均匀的骰子,则至少有一枚骰子的点数是6这个随机事 件的概率为 .
本次试验共有36个等可能的结果,其中至少有一枚骰子的点数是6(记为事件A)的结果有11个,所以P(A)= .
5.(2018湖北黄冈,14,3分)在-4,-2,1,2四个数中,随机取两个数分别作为函数y=ax2+bx+1中a,b的值,则该二 次函数图象恰好经过第一、二、四象限的概率为 .
解析 列举a,b所有可能的取值情况如下:
由上表可知,a,b所有可能的取值情况有12种,∵二次函数y=ax2+bx+1的图象恰好经过第一、二、四象限,且x=0时,y=1>0,∴ ∴a>0,b<0,且b2-4a>0,易知满足条件的a,b的值有2种情况,即a=1,b=-4或a=2,b=-4,∴二次函数图象恰好经过第一、二、四象限的概率为 = .
6.(2020吉林,16,5分)“中国结”是我国特有的手工编织工艺品,也是一种传统吉祥装饰物.如图,现有三 张正面印有“中国结”图案的不透明卡片A,B,C,卡片除正面图案不同外,其余均相同.将三张卡片正面 向下洗匀,小吉同学从中随机抽取一张卡片,记下图案后正面向下放回,洗匀后再从中随机抽取一张卡片. 请用画树状图或列表的方法,求小吉同学抽出的两张卡片中含有A卡片的概率.
解析 解法一:根据题意,画树状图如下. (3分)由树状图可以看出,所有等可能出现的结果共有9种,且抽出的两张卡片中含有A卡片的结果有5种,所以 P(小吉同学抽出的两张卡片中含有A卡片)= . (5分)解法二:根据题意,列表如下.
(3分)由表可以看出,所有等可能出现的结果共有9种,且抽出的两张卡片中含有A卡片的结果有5种,所以P(小 吉同学抽出的两张卡片中含有A卡片)= . (5分)
7.(2020江西,15,6分)某校合唱团为了开展线上“百人合唱一首歌”的“云演出”活动,需招收新成员.小 贤、小晴、小艺、小志四名同学报名参加了应聘活动,其中小贤、小艺来自七年级,小志、小晴来自八 年级.现对这四名同学采取随机抽取的方式进行线上面试.(1)若随机抽取一名同学,恰好抽到小艺同学的概率为 ;(2)若随机抽取两名同学,请用列表法或画树状图法求两名同学均来自八年级的概率.
解析 (1) .(2)解法一:根据题意,可以列表如下:
由上表可以得出,所有可能出现的结果共有12种,这些结果出现的可能性相等,“其中两名同学均来自八 年级”的结果共有2种,所以,P(两名同学均来自八年级)= = .解法二:根据题意,可以画出如下的树状图: 由树状图可以得出所有可能出现的结果共有12种,这些结果出现的可能性相等,“其中两名同学均来自
八年级”的结果共有2种,所以,P(两名同学均来自八年级)= = .
8.(2019贵州贵阳,19,10分)为落实立德树人的根本任务,加强思政、历史学科教师的专业化队伍建设.某 校计划从前来应聘的思政专业(一名研究生、一名本科生)、历史专业(一名研究生、一名本科生)的高 校毕业生中选聘教师,在政治思想审核合格的条件下,假设每位毕业生被录用的机会相等.(1)若从中只录用一人,恰好选到思政专业毕业生的概率是 ;(2)若从中录用两人,请用列表或画树状图的方法,求恰好选到的是一名思政研究生和一名历史本科生的 概率.
解析 (1) .(2)用a1,a2分别表示思政专业的研究生和本科生,用b1,b2分别表示历史专业的研究生和本科生.列表如下:
或画树状图如图: 共有12种等可能的结果,恰好选到的是一名思政研究生和一名历史本科生的结果有2种,所以P(选到一名 思政研究生和一名历史本科生)= = .
9.(2019内蒙古包头,21,8分)某校为了解九年级学生的体育达标情况,随机抽取50名九年级学生进行体育 达标项目测试,测试成绩如下表,请根据表中的信息,解答下列问题:
(1)该校九年级有450名学生,估计体育测试成绩为25分的学生人数;(2)该校体育老师要对本次抽测成绩为23分的甲、乙、丙、丁4名学生进行分组强化训练,要求两人一 组,求甲和乙恰好分在同一组的概率.(用列表或画树状图方法解答)
解析 (1)450× =162(人),∴九年级450名学生中,体育测试成绩为25分的学生人数约为162.(3分)(2)列表:
或画树状图如下: 所有可能出现的结果共有12种,∵丙丁分到一组时,甲乙也恰好在同一组,∴甲和乙恰好分在同一组的结 果有4种,∴甲和乙恰好分在同一组的概率P= . (8分)
1.(2020黑龙江齐齐哈尔,4,3分)一个质地均匀的小正方体,六个面分别标有数字“1”“2”“3”“4” “5”“6”,掷小正方体后,观察朝上一面的数字出现偶数的概率是 ( )A. B. C. D.
2.(2019浙江温州,4,4分)在同一副扑克牌中抽取2张“方块”,3张“梅花”,1张“红桃”.将这6张牌背面 朝上,从中任意抽取1张,是“红桃”的概率为 ( )A. B. C. D.
3.(2018内蒙古包头,4,3分)下列事件中,属于不可能事件的是 ( )A.某个数的绝对值大于0B.某个数的相反数等于它本身C.任意一个五边形的外角和等于540°D.长分别为3,4,6的三条线段能围成一个三角形
答案 C 某个数的绝对值大于0,是随机事件,某个数的相反数等于它本身,是随机事件,所以选项A,B不 符合题意;五边形的外角和等于360°,不可能等于540°,所以选项C是不可能事件,符合题意;选项D为必然 事件,不符合题意.故选C.
4.(2018内蒙古呼和浩特,5,3分)某学习小组做“用频率估计概率”的试验时,统计了某一结果出现的频 率,绘制了如下折线统计图,则符合这一结果的试验最有可能的是( ) A.袋中装有大小和质地都相同的3个红球和2个黄球,从中随机取一个,取到红球B.掷一枚质地均匀的正六面体骰子,向上的面的点数是偶数C.先后两次掷一枚质地均匀的硬币,两次都出现反面
D.先后两次掷一枚质地均匀的正六面体骰子,两次向上的面的点数之和是7或超过9
答案 D 从统计图中可以看出频率在 上下浮动,则可以估计事件发生的概率为 .选项A,取到红球的概率为 = ;选项B,向上的面的点数是偶数的概率为 = ;选项C,两次都出现反面的概率为 ;选项D,两次向上的面的点数之和是7或超过9的概率为 = .故选D.
5.(2020贵州贵阳,13,4分)在“抛掷正六面体”的试验中,正六面体的六个面分别标有数字“1”“2” “3”“4”“5”“6”,在试验次数很大时,数字“6”朝上的频率的变化趋势接近的值是 .
6.(2020新疆,12,5分)表中记录了某种苹果树苗在一定条件下移植成活的情况:
由此估计这种苹果树苗移植成活的概率为 .(精确到0.1)
解析 根据题中表格数据可知苹果树苗移植成活的频率近似值为0.9,所以估计这种苹果树苗移植成活的概率为0.9.故答案为0.9.
7.(2020天津,15,3分)不透明袋子中装有8个球,其中有3个红球、5个黑球,这些球除颜色外无其他差别.从 袋子中随机取出1个球,则它是红球的概率是 .
方法总结 根据概率的求法,找准两点:①全部情况的总数;②符合条件的情况的数目,二者的比值就是 某事件发生的概率.
8.(2019贵州贵阳,13,4分)一个袋中装有m个红球,10个黄球,n个白球,每个球除颜色外都相同,任意摸出一 个球,摸到黄球的概率与不是黄球的概率相同,那么m与n的关系是 .
答案 m+n=10
9.(2019四川成都,23,4分)一个盒子中装有10个红球和若干个白球,这些球除颜色外都相同.再往该盒子中 放入5个相同的白球,摇匀后从中随机摸出一个球,若摸到白球的概率为 ,则盒子中原有的白球的个数为 .
解析 设盒子中原有白球x个,由题意得(x+5)∶(10+x+5)=5∶7,所以x=20,经检验,x=20是原方程的解,且 符合题意,所以盒子中原有的白球的个数为20.
10.(2018内蒙古呼和浩特,14,3分)已知函数y=(2k-1)x+4(k为常数),若从-3≤k≤3中任取k值,则得到的函数 是具有性质“y随x增加而增加”的一次函数的概率为 .
1.(2020内蒙古包头,17,3分)一个不透明的盒子里放置三张完全相同的卡片,分别标有数字1,2,3.随机抽取 1张,放回后再随机抽取1张,则抽得的第二张卡片上的数字大于第一张卡片上的数字的概率为 .
解析 用列表法表示所有可能出现的结果,如下:
共有9种等可能的结果,其中第二张卡片上的数字大于第一张卡片上的数字的有(1,2),(1,3),(2,3),共3种情 况,故P= = .
2.(2020重庆A卷,15,4分)现有四张正面分别标有数字-1,1,2,3的不透明卡片,它们除数字外其余完全相同, 将它们背面朝上洗均匀,随机抽取一张,记下数字后放回,背面朝上洗均匀,再随机抽取一张记下数字,前 后两次抽取的数字分别记为m,n,则点P(m,n)在第二象限的概率为 .
3.(2020宁夏,11,3分)有三张大小、形状完全相同的卡片.卡片上分别写有数字4、5、6,从这三张卡片中 随机先后不放回地抽取两张,则两次抽出数字之和为奇数的概率是 .
4.(2019新疆,13,5分)同时掷两枚质地均匀的骰子,两枚骰子点数之和小于5的概率是 .
5.(2020四川成都,17,8分)2021年,成都将举办世界大学生运动会,这是在中国西部第一次举办的世界综合 性运动会.目前,运动会相关准备工作正在有序进行,比赛项目已经确定.某校体育社团随机调查了部分同 学在田径、跳水、篮球、游泳四种比赛项目中选择一种观看的意愿,并根据调查结果绘制成了如下两 幅不完整的统计图. 根据以上信息,解答下列问题:(1)这次被调查的同学共有 人;
(2)扇形统计图中“篮球”对应的扇形圆心角的度数为 ;(3)现拟从甲、乙、丙、丁四人中任选两名同学担任大运会志愿者,请利用画树状图或列表的方法,求恰 好选中甲、乙两位同学的概率.
解析 (1)根据两个统计图中选择观看跳水项目的同学的信息可得,这次被调查的同学共有 =180(人).故填180.(2)依题得,选择观看篮球项目的同学有180×(1-20%-15%-30%)=63(人),故所对应的扇形圆心角度数为 ×360°=126°.故填126°.(3)画树状图如图所示: 总共有12种等可能的结果,恰好选中甲、乙两位同学的结果有2种,故所求概率为 = .
6.(2020云南,19,7分)甲、乙两个家庭来到以“生态资源,绿色旅游”为产业的美丽云南,各自随机选择到 大理、丽江、西双版纳三个城市中的一个城市旅游.假设这两个家庭选择到哪个城市旅游不受任何因 素影响,上述三个城市中的每一个被选到的可能性相同,甲、乙两个家庭选择到上述三个城市中的同一 个城市旅游的概率为P.(1)直接写出甲家庭选择到大理旅游的概率;(2)用列表法或画树状图法(树状图也称树形图)中的一种方法,求P的值.
解析 (1)甲家庭选择到大理旅游的概率为 . (2分)(2)记大理、丽江、西双版纳分别为A,B,C.解法一:列表如下.
所有可能出现的结果共有9种. (5分)解法二:画树形图(树状图)如下. 所有可能出现的结果共有9种. (5分)由列表法或画树形图(树状图)法可知,在9种可能出现的结果中,它们出现的可能性相等.其中选择旅游城 市是同一个城市的结果有3种,
∴P= = .答:甲、乙两个家庭选择到同一个城市旅游的概率是 . (7分)
7.(2020辽宁营口,20,10分)随着“新冠肺炎”疫情防控形势日渐好转,各地开始复工复学.某校复学后成 立“防疫志愿者服务队”,设立四个“服务监督岗”:①洗手监督岗,②戴口罩监督岗,③就餐监督岗,④ 操场活动监督岗.李老师和王老师报名参加了志愿者服务工作,学校将报名的志愿者随机分配到四个监 督岗.(1)李老师被分配到“洗手监督岗”的概率为 ;(2)用列表法或画树状图法求李老师和王老师被分配到同一个监督岗的概率.
(6分)由表格可以看出,随机将李老师和王老师分配到四个监督岗,可能出现的结果共有16种,并且它们出现的 可能性相等.其中李老师和王老师被分配到同一个监督岗的结果有4种,即(①①),(②②),(③③),(④④), (9分)∴P(李老师和王老师被分配到同一个监督岗)= = .(10分)解法二:画树状图如图所示:
(6分)由树状图可以看出,随机将李老师和王老师分配到四个监督岗,可能出现的结果共有16种,并且它们出现 的可能性相等.其中李老师和王老师被分配到同一个监督岗的结果有4种,即①①,②②,③③,④④. (9分)∴P(李老师和王老师被分配到同一个监督岗)= = . (10分)
8.(2020陕西,22,7分)小亮和小丽进行摸球试验.他们在一个不透明的空布袋内,放入两个红球,一个白球 和一个黄球,共四个小球.这些小球除颜色外其他都相同.试验规则:先将布袋内的小球摇匀,再从中随机 摸出一个小球,记下颜色后放回,称为摸球一次.(1)小亮随机摸球10次,其中6次摸出的是红球,求这10次中摸出红球的频率;(2)若小丽随机摸球两次,请利用画树状图或列表的方法,求这两次摸出的球中一个是白球、一个是黄球 的概率.
解析 (1)摸出红球的频率为 = . (3分)(2)列表如下:
(5分)由上表可知,共有16种等可能的结果,其中摸出一白一黄的结果有2种,∴P(摸出一白一黄)= = . (7分)
9.(2020四川南充,19,8分)今年,全球疫情大爆发,我国派遣医疗专家组对一些国家进行医疗援助.某批次 派出20人组成的专家组,分别赴A、B、C、D四个国家开展援助工作,其人员分布情况如统计图(不完整) 所示: (1)计算赴B国女专家和D国男专家人数,并将条形统计图补充完整;(2)根据需要,从赴A国的专家中,随机抽取两名专家对当地医疗团队进行培训,求所抽取的两名专家恰好
解析 (1)赴B国女专家为20×40%-5=3(人); (1分)赴D国男专家为20×(1-25%-40%-20%)-2=1(人). (3分)(注:补全条形图如图所示) (4分)(2)从5名专家中,随机抽取两名专家的所有可能结果如下:
(6分)由上表可知,随机抽取两名专家的所有可能情况有20种,并且出现的可能性相等,其中恰好抽取一男一女 的情况有12种,则所抽取的两名专家恰好是一男一女的概率P= = . (8分)
10.(2020云南昆明,18,7分)有一个可自由转动的转盘,被分成了三个大小相同的扇形,分别标有数字2,4,6; 另有一个不透明的瓶子,装有分别标有数字1,3,5的三个完全相同的小球.小杰先转动一次转盘,停止后记 下指针指向的数字(若指针指在分界线上则重转),小玉再从瓶子中随机取出一个小球,记下小球上的数 字.(1)请用列表或画树状图的方法(选其中一种)表示出所有可能出现的结果;(2)若得到的两数字之和是3的倍数,则小杰赢;若得到的两数字之和是7的倍数,则小玉赢.此游戏公平吗? 为什么?
解析 (1)列表如下:
(3分)所以,可能的结果共有9种,它们出现的可能性相等. (4分)(2)公平.理由:数字之和是3的倍数记为事件A,结果有3种,即(2,1),(4,5),(6,3),∴P(A)= = . (5分)数字之和是7的倍数记为事件B,结果有3种,即(2,5),(4,3),(6,1),∴P(B)= = . (6分) ∵P(A)=P(B),∴此游戏公平. (7分)
11.(2020贵州贵阳,20,10分)“2020第二届贵阳市应急科普知识大赛”的比赛中有一个抽奖活动.规则是: 准备3张大小一样,背面完全相同的卡片,3张卡片的正面所写内容分别是《消防知识手册》《辞海》 《辞海》,将它们背面朝上洗匀后任意抽出一张,抽到卡片后可以免费领取卡片上相应的书籍.(1)在上面的活动中,如果从中随机抽出一张卡片,记下内容后不放回,再随机抽出一张卡片,请用列表或 画树状图的方法,求恰好抽到2张卡片都是《辞海》的概率;(2)再添加几张和原来一样的《消防知识手册》卡片,将所有卡片背面朝上洗匀后,任意抽出一张,使得抽 到《消防知识手册》卡片的概率为 ,那么应添加多少张《消防知识手册》卡片?请说明理由.
解析 (1)先将正面所写内容是《消防知识手册》《辞海》《辞海》的卡片分别记作A,B1,B2,然后列表 如下:
总共有6种结果,每种结果出现的可能性相同,而2张卡片都是《辞海》的有2种:(B2,B1),(B1,B2),所以,P(2张卡片都是《辞海》)= = .(2)设应添加x张《消防知识手册》卡片,由题意得: = ,解得x=4.经检验,x=4是原方程的解,且符合题意.答:应添加4张《消防知识手册》卡片.
12.(2019甘肃兰州,21,6分)2019年5月,以“寻根国学,传承文明”为主题的兰州市第三届“国学少年强— —国学知识挑战赛”总决赛拉开帷幕,小明晋级了总决赛.比赛过程分两个环节,参赛选手须在每个环节 中各选择一道题目.第一环节:写字注音、成语故事、国学常识、成语接龙(分别用A1,A2,A3,A4表示);第二环节:成语听写、诗词对句、经典诵读(分别用B1,B2,B3表示).(1)请用画树状图或列表的方法表示小明参加总决赛抽取题目的所有可能结果;(2)求小明参加总决赛抽取题目都是成语题目(成语故事、成语接龙、成语听写)的概率.
解析 (1)小明参加总决赛抽取题目的所有可能结果如下表:
(2)由题可知,A2,A4,B1代表成语题目,所以小明参加总决赛抽取题目都是成语题目的有A2B1,A4B1两种情况, 由(1)知总共有12种情况,所以所求概率为 .
13.(2019吉林长春,16,6分)一个不透明的口袋中有三个球,每个小球上只标有一个汉字,分别是“家” “家”“乐”,除汉字外其余均相同.小新同学从口袋中随机摸出一个小球,记下汉字后放回并搅匀;再 从口袋中随机摸出一个小球记下汉字.用画树状图(或列表)的方法,求小新同学两次摸出小球上的汉字 相同的概率.
解析 画树状图如图: 一共有9种等可能结果,其中两次摸出小球上的汉字相同的情况有5种,所以所求概率为 .答:小新同学两次摸出小球上的汉字相同的概率是 .
思路分析 依据题意画出树状图,找出所有可能出现的情况以及小新两次都摸到标有相同汉字的小球 的情况,最后利用概率公式进行计算即可.
14.(2019山东潍坊,21,9分)如图所示,有一个可以自由转动的转盘,其盘面分为4等份,在每一等份分别标 有对应的数字2,3,4,5.小明打算自由转动转盘10次,现已经转动了8次,每一次停止后,小明将指针所指数 字记录如下:
(1)求前8次的指针所指数字的平均数;(2)小明继续自由转动转盘2次,判断是否可能发生“这10次的指针所指数字的平均数不小于3.3,且不大 于3.5”的结果.若有可能,计算发生此结果的概率,并写出计算过程;若不可能,说明理由.(指针指向盘面 等分线时为无效转次)
解析 (1) =3.5.故前8次的指针所指数字的平均数为3.5. (3分)(2)能发生. (4分)若这10次的指针所指数字的平均数不小于3.3,且不大于3.5,则所指数字之和应不小于33,且不大于35,而 前8次的所指数字之和为28,所以最后两次的所指数字之和应不小于5,且不大于7. (5分)第9次和第10次指针所指数字如下表所示:
(8分)或第9次和第10次指针所指数字树状图如下: (8分)一共有16种等可能结果,其中第9次和第10次指针所指数字之和不小于5,且不大于7的有9种结果,故其概 率为 .因此,这10次的指针所指数字的平均数不小于3.3,且不大于3.5的概率为 . (9分)
思路分析 (1)根据平均数的定义求解可得;(2)由这10次的指针所指数字的平均数不小于3.3,且不大于3. 5知后两次指针所指数字之和要满足不小于5,且不大于7,再列表或画树状图求解可得.
15.(2019吉林,16,5分)甲口袋中装有红色、绿色两把扇子,这两把扇子除颜色外无其他差别;乙口袋中装 有红色、绿色两条手绢,这两条手绢除颜色外无其他差别.从甲口袋中随机取出一把扇子,从乙口袋中随 机取出一条手绢.用画树状图或列表的方法,求取出的扇子和手绢都是红色的概率.
解析 解法一:根据题意,画树状图如下: (3分)由树状图可以看出,所有等可能出现的结果共有4种,且取出的扇子和手绢都是红色的结果有1种,所以P (扇子和手绢都是红色)= . (5分)解法二:根据题意,列表如下:
(3分)由表可以看出,所有等可能出现的结果共有4种,且取出的扇子和手绢都是红色的结果有1种,所以P(扇子 和手绢都是红色)= . (5分)
16.(2018辽宁沈阳,19,8分)经过校园某路口的行人,可能左转,也可能直行或右转.假设这三种可能性相同, 现有小明和小亮两人经过该路口,请用列表法或画树状图法,求两人之中至少有一人直行的概率.
解析 依据题意,列表得
或画树状图得 由表格(或树状图)可知,共有9种可能出现的结果,每种结果出现的可能性相同,其中两人中至少有一人直 行的结果有5种,分别为(左转,直行),(直行,左转),(直行,直行),(直行,右转),(右转,直行).∴P(两人中至少有 一人直行)= .
A组 2018—2020年模拟·基础题组时间:45分钟 分值:55分一、选择题(每小题3分,共9分)
1.(2019江西南昌一模,2)在不透明的袋子中装有9个白球和1个红球,它们除颜色外其余都相同,现从袋子 中随机摸出一个球,摸出的球是白球,则该事件是 ( )A.必然事件 B.不可能事件C.随机事件 D.以上都有可能
答案 C “在不透明的袋子中装有9个白球和1个红球,它们除颜色外其余都相同,现从袋子中随机摸 出一个球,摸出的球是白球”这一事件是随机事件,故选C.
2.(2020辽宁大连金州一模,8)不透明袋子中装有红、绿小球各2个,除颜色外无其他差别.随机摸出一个 小球后,不放回,再随机摸出一个,两次都摸到红球的概率为 ( )A. B. C. D.
3.(2019云南曲靖一模,4)如图,这是一幅2018年俄罗斯世界杯的长方形宣传画,长为4 m,宽为2 m.为测量 画上世界杯图案的面积,现将宣传画平铺在地上,向长方形宣传画内随机投掷骰子(假设骰子落在长方形 内的每一点都是等可能的),经过大量重复投掷试验,发现骰子落在世界杯图案中的频率稳定在常数0.4. 由此可估计宣传画上世界杯图案的面积为 ( ) A.2.4 m2 B.3.2 m2 C.4.8 m2 D.7.2 m2
答案 B ∵骰子落在世界杯图案中的频率稳定在常数0.4,∴估计骰子落在世界杯图案中的概率为0.4, ∴估计宣传画上世界杯图案的面积为0.4×(4×2)=3.2(m2).故选B.
二、填空题(每小题3分,共15分)4.(2020天津河北3月模拟,15)在单词“banana”中随机选取一个字母,选到的字母是“a”的概率是 .
5.(2020天津河北模拟,14)从n个苹果和4个雪梨中任选1个,若选中苹果的概率是 ,则n的值是 .
6.(2019天津河北一模,15)在“绿水青山就是金山银山”这句话中任选一个汉字,这个字是“山”的概率 是 .
7.(2019四川成都邛崃二诊,22)2019年2月上旬某市空气质量指数(AQI)(单位:μg/m3)如下表所示,空气质 量指数不大于100表示空气质量优良.
如果小王2月上旬到该市度假一次,那么他在该市度假3天,空气质量都是优良的概率是 .
8.(2018湖北武汉四校3月联考,14)一个不透明的袋中共有5个小球,分别为2个红球和3个黄球,它们除颜 色外完全相同,随机摸出两个小球,则摸出两个颜色不同小球的概率是 .
解析 画树状图如下: 由树状图可知,共有20种等可能结果,其中摸出的小球颜色不同的有12种结果,∴两次摸出的小球颜色不同的概率为 = .
三、解答题(共31分)9.(2020甘肃兰州一诊,22)为了参加学校组织的志愿服务活动,八年级1班需要在A,B,C,D四名学生中随机 选派2名学生参加,请用列表或画树状图的方法求出恰好选派A和C两位同学参加的概率.
10.(2020吉林长春一模,16)在一个不透明的盒子中装有三张卡片,正面分别标有数字1,2,7,这些卡片除数 字不同外其余均相同.洗匀后,小强从盒子中随机抽取一张卡片,记下数字后放回,洗匀后再随机抽取一张 卡片.用画树状图或列表的方法求两次抽取的卡片上数字之和为偶数的概率.
解析 根据题意,列表如下:
所以P(两次抽取的卡片上数字之和为偶数)= .
11.(2019云南昆明官渡一模,18)四张扑克牌的点数分别是2,5,6,8,除点数不同外,其余都相同,将它们洗匀 后背面朝上放在桌上.(1)若从中随机抽取一张牌,则抽出的牌的点数是偶数的概率为 ;(2)若随机抽取一张牌且不放回,接着再抽取一张牌,请用列表法或画树状图法(只选其中一种)表示出所 有可能出现的结果,并求所抽两张牌的点数都是偶数的概率.
从表格可以看出,共有12种结果,每种结果出现的可能性相同,其中两张牌的点数都是偶数的结果有6种,所以这两张牌的点数都是偶数的概率为 = .
12.(2019陕西西安工大附中一模,21)小昕的口袋中有5把相似的钥匙,其中2把钥匙(记为A1,A2)能打开教 室前门锁,而剩余的3把钥匙(记为B1,B2,B3)不能打开教室前门锁.(1)小昕从口袋中随便摸出一把钥匙就能打开教室前门锁的概率是 ;(2)请用画树状图或列表的方法,求出小昕从口袋中第一次随机摸出的一把钥匙不能打开教室前门锁(摸 出的钥匙不再放回),而第二次随机摸出的一把钥匙正好能打开教室前门锁的概率.
解析 (1)P(取出A1或A2)= .故填 .(2)画树状图得: ∵共有20种等可能的结果,第一次随机摸出的一把钥匙不能打开教室前门锁(摸出的钥匙不再放回),而 第二次随机摸出的一把钥匙正好能打开教室前门锁有6种可能,∴第一次随机摸出的一把钥匙不能打开教室前门锁(摸出的钥匙不再放回),而第二次随机摸出的一把钥 匙正好能打开教室前门锁的概率为 = .
B组 2018—2020年模拟·提升题组时间:45分钟 分值:55分一、选择题(每小题3分,共18分)
1.(2020内蒙古包头4月模拟,10)从1,2,3,4中任取两个不同的数,分别记为a和b,则a2+b2>19的概率是 ( )A. B. C. D.
答案 D 画树状图如图所示, 由图知任取两个不同的数,共有12种等可能的结果,满足a2+b2>19的结果有4种,∴a2+b2>19的概率是 = ,故选D.
2.(2020黑龙江绥化一模,5)有三张正面分别写有数字-2,1,3的卡片,它们背面完全相同,现将这三张卡片背 面朝上洗匀,然后随机抽取一张,以其正面数字作为a的值,然后把这张卡片放回去洗匀,再从三张卡片中 随机抽取一张,以其正面的数字作为b的值,则点(a,b)在第一象限的概率为 ( )A. B. C. D.
答案 D 用列表法表示(a,b)所有可能出现的结果如下:
由表知,共有9种等可能结果,其中点(a,b)在第一象限的结果有4种,所以点(a,b)在第一象限的概率为 ,故选D.
3.(2020湖北武汉青山备考,7)从1,2,3,6这四个数中任取两个数,分别记为m、n,那么点(m,n)在函数y= 图象上的概率是 ( )A. B. C. D.
答案 B 画树状图如图所示, 由图知共有12种等可能的结果,满足点(m,n)在函数y= 图象上的点有(1,6),(2,3),(3,2),(6,1),共4个,∴点(m,n)在函数y= 图象上的概率是 = .故选B.
4.(2019湖北武汉青山一模,6)甲、乙、丙三人相互传球,由甲开始发球,作为第一次传球,第二次传球后球 回到甲手中的概率是( )A. B. C. D.
答案 A 画树状图如图: 由树状图知,共有4种等可能结果,其中第二次传球后球回到甲手中的结果有2种,所以第二次传球后球回 到甲手中的概率为 = ,故选A.
5.(2019辽宁铁岭一模,4)如图,共有12个大小相同的小正方形,其中阴影部分的5个小正方形是一个正方 体的表面展开图的一部分.现从其余的小正方形中任取一个涂上阴影,则能构成这个正方体的表面展开 图的概率是 ( ) A. B. C. D.
答案 D 因为共有12个大小相同的小正方形,其中阴影部分的5个小正方形是一个正方体的表面展开 图的一部分,所以剩下7个小正方形.在其余的7个小正方形中任取一个涂上阴影,能构成这个正方体的表 面展开图的小正方形有4个,因此从其余的小正方形中任取一个涂上阴影,能构成这个正方体的表面展开 图的概率是 .故选D.
6.(2018天津红桥一模,4)在一个不透明的口袋中装有4个红球和若干个白球,它们除颜色外其他均相同, 从袋中随机摸出一个球,记下颜色后放回.通过大量重复摸球试验后发现,摸到红球的频率在25%附近摆 动,则口袋中的白球有 ( )A.12个 B.13个 C.15个 D.16个
二、填空题(每小题3分,共12分)7.(2020四川成都青白江一诊,22)在试制某种洗发液新品种时,需要选用两种不同的添加剂.现有芳香度 分别为0,1,2,3,4,5的六种添加剂可供选用.根据试验设计原理,通常要先从芳香度为0,1,2的三种添加剂中 随机选取一种,再从芳香度为3,4,5的三种添加剂中随机选取一种,进行搭配试验,则芳香度之和等于5的 概率为 .
8.(2020广西崇左江州一模,16)书架上有3本小说、2本散文,从中随机抽取2本,都是小说的概率是 .
9.(2019黑龙江哈尔滨香坊一模,19)在一个不透明的布袋中装有三个小球,小球上分别标有数字-2,1,2,它 们除了数字不同外,其他都完全相同.小红先从布袋中随机摸出一个小球,记下数字作为k的值,再把此球 放回袋中搅匀,再随机摸出一个小球,记下数字作为b的值,则直线y=kx+b不经过第二象限的概率是 .
共有9种等可能的结果,其中符合条件的结果数为2,所以直线y=kx+b不经过第二象限的概率为 .
10.(2019内蒙古呼和浩特4月模拟,13)某中学组织的“红歌大赛”中60名选手的成绩统计如图,已知成绩 在94.5分以上的选手中男生和女生各占一半,学校从中随机确定2名参加市“红歌大赛”,则恰好选到一 名男生和一名女生的概率为 .
三、解答题(共25分)11.(2020江西南昌二模,15)读高中的小明从家到学校需要中途转一趟车,从家到站台M可乘A,B,C三路车 (小明乘A,B,C三路车的可能性相同),到了站台M后可以转乘D路或E路车直接到学校(小明乘D,E两路车 的可能性相同).(1)“小明从家到站台M乘坐A路车”是 事件,小明从站台M到学校乘坐F路车的概率为 ;(2)请用列表或画树状图的方法求小明先乘坐A路车,再转乘D路或E路车到学校的概率.
解析 (1)随机;0.(2)画树状图如图: 由图可知,共有6种等可能的结果,其中小明先乘坐A路车,再转乘D路或E路车到学校的结果有2种,∴小明先乘坐A路车,再转乘D路或E路车到学校的概率为 = .
12.(2019新疆喀什一模,21)已知在一个不透明的口袋中有4个形状、大小、材质完全相同的球,其中1个 红色球,3个黄色球.(1)从口袋中随机取出一个球(不放回),接着再取出一个球,请用画树形图或列表的方法求取出的两个球 都是黄色球的概率;(2)小明往该口袋中又放入红色球和黄色球若干个,一段时间后他记不清具体放入红色球和黄色球的个 数,只记得一种球的个数比另一种球的个数多1,且从口袋中随机取出一个球,该球是黄色球的概率为 ,请问小明又放入该口袋中红色球和黄色球各多少个?
解析 (1)两次取球的树形图如图: ∴共有12种等可能结果,两次都取到黄色球的结果数为6,∴P(两个球都是黄色球)= = .(2)∵又放入口袋的两种球中,一种球的个数比另一种球的个数多1,∴又放入口袋中的红色球的个数只有两种可能.①若设小明又放入红色球m个,则放入黄色球(m+1)个,
故口袋中球的总数为5+2m,于是有 = ,则m=2;②若设小明又放入红色球(m+1)个,则放入黄色球m个,由 = ,得m=-1,不合题意,舍去.所以,小明又放入了2个红色球和3个黄色球.
一、选择题(每小题5分,共25分)
1.(2019辽宁盘锦,8)下列说法正确的是 ( )A.方差越大,数据波动越小B.了解辽宁省初中生身高情况适合采用全面调查C.抛掷一枚硬币,正面向上是必然事件D.用长为3 cm,5 cm,9 cm的三条线段围成一个三角形是不可能事件
答案 D 方差越大,数据波动越大,故选项A中的说法错误;了解辽宁省初中生身高情况适合采用抽样 调查,故选项B中的说法错误;抛掷一枚硬币,正面向上是随机事件,故选项C中的说法错误;用长为3 cm,5 cm,9 cm的三条线段围成一个三角形是不可能事件,故选项D中的说法正确.故选D.
2.(2019黑龙江大庆,7)某企业1~6月份利润的变化情况如图所示,以下说法与图中反映的信息相符的是 ( ) A.1~6月份利润的众数是130万元B.1~6月份利润的中位数是130万元C.1~6月份利润的平均数是130万元D.1~6月份利润的极差是40万元
答案 D 1~6月份利润的众数是120万元,故A选项错误;1~6月份利润的中位数是125万元,故B选项错 误;1~6月份利润的平均数是 ×(110+120+130+120+140+150)= 万元,故C选项错误;1~6月份利润的极差是150-110=40万元,故D选项正确.故选D.
3.(2019贵州毕节,14)平行四边形ABCD中,AC、BD是两条对角线,现从以下四个关系①AB=BC;②AC= BD;③AC⊥BD;④AB⊥BC中随机取出一个作为条件,即可推出平行四边形ABCD是菱形的概率为 ( )A. B. C. D.1
4.(2019贵州铜仁,4)某班17名女同学的跳远成绩如下表所示:
这些女同学跳远成绩的众数和中位数分别是 ( ),1.75 ,,1.70 ,1.725
答案 B 由题表可知,1.75出现次数最多,所以众数为1.75.中位数为将这组数据按从小到大的顺序排列后的第9个数据,所以中位数为1.70.故选B.
5.(2019湖北荆门,7)投掷一枚质地均匀的骰子两次,向上一面的点数依次记为a,b.那么方程x2+ax+b=0有 解的概率是 ( )A. B. C. D.
答案 D 画树状图如图. 由图可知,共有36种等可能的结果数,其中使a2-4b≥0,即a2≥4b的有19种,∴方程x2+ax+b=0有解的概率是 ,故选D.
二、填空题(每小题5分,共20分)6.(2019辽宁营口,14)在一次青年歌手演唱比赛中,10位评委给某位歌手的打分分别是:9.5,9.8,9.4,9.5,9.6, 9.3,9.6,9.4,9.3,9.4,则这组数据的众数是 .
解析 9.4出现了3次,出现的次数最多,故众数是9.4.
7.(2019内蒙古通辽,11)下图是我市6月份某7天的最高气温折线统计图,则这些最高气温的中位数是 ℃.
解析 将这7天的最高气温从小到大排列为24,25,26,27,28,28,29,故中位数为27 ℃.
8.(2019广西贵港,16)若随机掷一枚均匀的骰子,骰子的6个面上分别刻有1,2,3,4,5,6点,则点数不小于3的 概率是 .
9.(2019湖北孝感,14)董永社区在创建全国卫生城市的活动中,随机检查了本社区部分住户五月份某周内 “垃圾分类”的实施情况,将他们一周内实施“垃圾分类”的户数等数据绘制成了两幅不完全的统计 图(A.小于5天;B.5天;C.6天;D.7天),则扇形统计图中B部分所对应的扇形圆心角的度数是 .
三、解答题(共4小题,共55分)10.(10分)(2020山东青岛,17)小颖和小亮都想去观看“垃圾分类”宣传演出,但只有一张入场券,于是他 们设计了一个“配紫色”游戏:A,B是两个可以自由转动的转盘,每个转盘都被分成面积相等的几个扇 形,同时转动两个转盘,如果其中一个转盘转出了红色,另一个转盘转出了蓝色,那么可以配成紫色.若配 成紫色,则小颖去观看,否则小亮去观看.这个游戏对双方公平吗?请说明理由.
解析 这个游戏对双方公平.理由如下:画树状图如下: 由树状图可知,所有等可能出现的结果共有6种,其中能配成紫色的结果数为3,∴P(小颖去)= = ,P(小亮去)= = .∵P(小颖去)=P(小亮去),
∴这个游戏对双方公平.
11.(15分)(2020山东青岛,19)某校为调查学生对海洋科普知识的了解情况,从全校学生中随机抽取n名学 生进行测试,测试成绩进行整理后分成五组,并绘制成如下的频数直方图和扇形统计图. 请根据图中信息解答下列问题:(1)补全频数直方图;(2)在扇形统计图中,“70~80”这组的百分比m= ;
(3)已知“80~90”这组的数据如下:81,83,84,85,85,86,86,86,87,88,88,89,抽取的n名学生测试成绩的中位 数是 分;(4)若成绩达到80分以上(含80分)为优秀,请你估计全校1 200名学生对海洋科普知识了解情况为优秀的 学生人数.
解析 (1)由统计图可知“60~70”这组的人数为8,所占的百分比为16%,∴n=8÷16%=50,∴“90~100”这组的人数为50-4-8-10-12=16.补全频数直方图如下: (2)∵n=50,“70~80”这组的人数为10,∴“70~80”这组的百分比为 ×100%=20%,即m=20%.
(3)由(1)知n=50,故这50名学生测试成绩的中位数是排序后第25,26个数据的平均数,结合频数直方图及 题意可知第25,26个数据分别为84,85,∴抽取的n名学生测试成绩的中位数是 =84.5(分).(4)∵成绩达到80分以上(含80分)的百分比为 ×100%=56%,∴估计全校1 200名学生对海洋科普知识了解情况为优秀的学生人数为1 200×56%=672.
12.(15分)(2019贵州毕节,23)某地区在所有中学开展《老师,我想对你说》心灵信箱活动,为师生之间的 沟通增设了一个书面交流的渠道.为了解两年来活动开展的情况,某课题组从全地区随机抽取部分中学 生进行问卷调查.对“两年来,你通过心灵信箱给老师总共投递过几封信?”这一调查项设有四个回答选 项,选项A:没有投过;选项B:一封;选项C:两封;选项D:三封及以上.根据接受问卷调查学生的回答,统计出 各选项的人数以及所占百分比,分别绘制成如下条形统计图和扇形统计图:
(1)此次抽样调查了 名学生,条形统计图中m= ,n= ;(2)请将条形统计图补全;(3)接受问卷调查的学生在活动中投出的信件总数至少有 封;(4)全地区中学生共有110 000名,由此次调查估算,在此项活动中,全地区给老师投过信件的学生约有多 少名.
解析 (1)此次调查的总人数为150÷30%=500,则m=500×45%=225,n=500×5%=25,故答案为500,225,25.(2)C选项人数为500×20%=100,补全图形如下: (3)1×150+2×100+3×25=425(封).答:接受问卷调查的学生在活动中投出的信件总数至少有425封.
故答案为425.(4)由此次调查估算,在此项活动中,全地区给老师投过信件的学生约有110 000×(1-45%)=60 500(名).
13.(15分)(2019辽宁抚顺,20)为提升学生的艺术素养,某校计划开设四门选修课程:声乐、舞蹈、书法、 摄影.要求每名学生必须选修且只能选修一门课程,为保证计划的有效实施,学校随机对部分学生进行了 一次调查,并将调査结果绘制成如下不完整的统计表和统计图.学生选修课程统计表
根据以上信息,解答下列问题:(1)m= ,b= ;(2)求出a的值并补全条形统计图;(3)该校有1 500名学生,请你估计选修“声乐”课程的学生有多少名;(4)七(1)班和七(2)班各有2人选修“舞蹈”课程且有舞蹈基础,学校准备从这4人中随机抽取2人编排 “舞蹈”在开班仪式上表演,请用列表法或画树状图的方法求所抽取的2人恰好来自同一个班级的概率.
解析 (1)m=8÷16%=50,b%= ×100%=28%,即b=28.故答案为50,28.(2)a=50×24%=12,补全图形如下: (3)估计选修“声乐”课程的学生有1 500×28%=420(人).
数学25.1.2 概率达标测试: 这是一份数学25.1.2 概率达标测试,共13页。试卷主要包含了求下列事件的概率等内容,欢迎下载使用。
中考数学一轮复习课时练习第31课时 概 率 (含答案): 这是一份中考数学一轮复习课时练习第31课时 概 率 (含答案),共15页。试卷主要包含了 下列事件为必然事件的是,1).等内容,欢迎下载使用。
中考数学全面突破:第十九讲 概 率 含解析答案: 这是一份中考数学全面突破:第十九讲 概 率 含解析答案,共11页。












