




2021版《5年中考3年模拟》全国版中考数学:§4.5 特殊的平行四边形
展开1.(2019重庆A卷,5,4分)下列命题正确的是 ( )A.有一个角是直角的平行四边形是矩形B.四条边相等的四边形是矩形C.有一组邻边相等的平行四边形是矩形D.对角线相等的四边形是矩形
答案 A ∵有一个角是直角的平行四边形是矩形,∴A选项正确;∵四条边相等的四边形是菱形,∴B选项错误;∵有一组邻边相等的平行四边形是菱形,∴C选项错误;∵对角线相等的平行四边形是矩形,∴D选项错误.故选A.
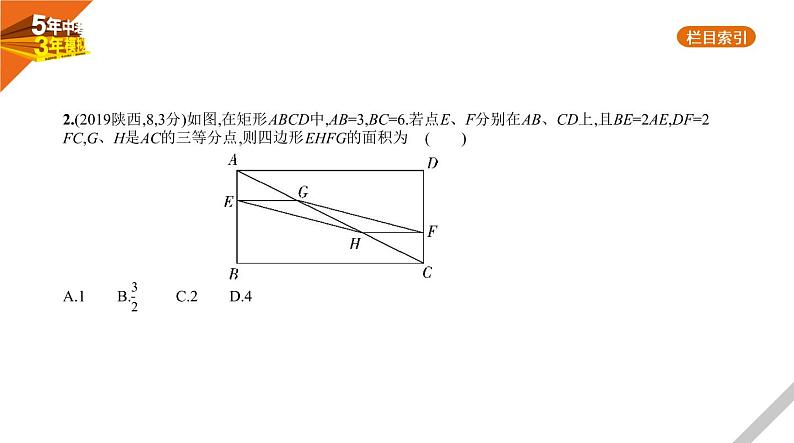
2.(2019陕西,8,3分)如图,在矩形ABCD中,AB=3,BC=6.若点E、F分别在AB、CD上,且BE=2AE,DF=2 FC,G、H是AC的三等分点,则四边形EHFG的面积为 ( ) A.1 B. C.2 D.4
答案 C 在矩形ABCD中,AD=BC=6,AB=CD=3,∵BE=2AE,∴E是AB的三等分点(靠近点A),∵G是AC的三等分点(靠近点A),∴EG∥BC且EG= BC=2.同理可得HF∥AD且HF= AD=2.∴四边形EHFG为平行四边形.又EG与HF间的距离为 AB,∴S四边形EHFG=2× AB=2.
3.(2020云南,6,3分)已知四边形ABCD是矩形,点E是矩形ABCD的边上的点,且EA=EC.若AB=6,AC=2 ,则DE的长是 .
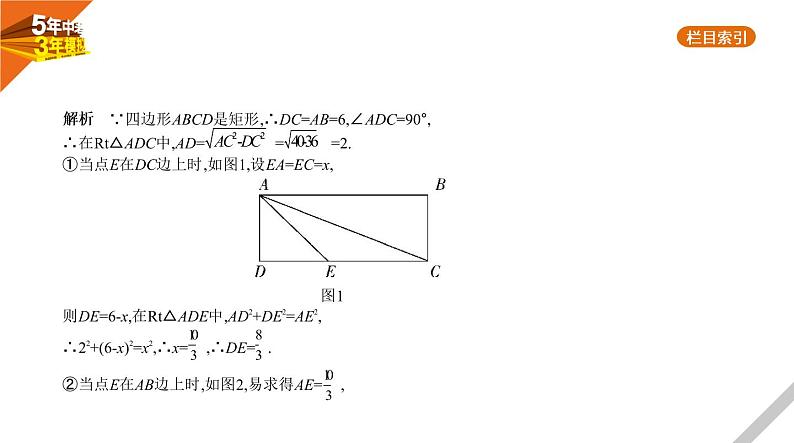
解析 ∵四边形ABCD是矩形,∴DC=AB=6,∠ADC=90°,∴在Rt△ADC中,AD= = =2.①当点E在DC边上时,如图1,设EA=EC=x, 图1则DE=6-x,在Rt△ADE中,AD2+DE2=AE2,∴22+(6-x)2=x2,∴x= ,∴DE= .②当点E在AB边上时,如图2,易求得AE= ,
∴在Rt△ADE中,DE= = .∴DE的长为 或 . 图2
解后反思 本题主要考查矩形的性质,勾股定理以及分类讨论的思想,因为点E的位置不确定,需根据EA =EC,讨论点E在边AB和边DC上的情况,分别求DE的长.
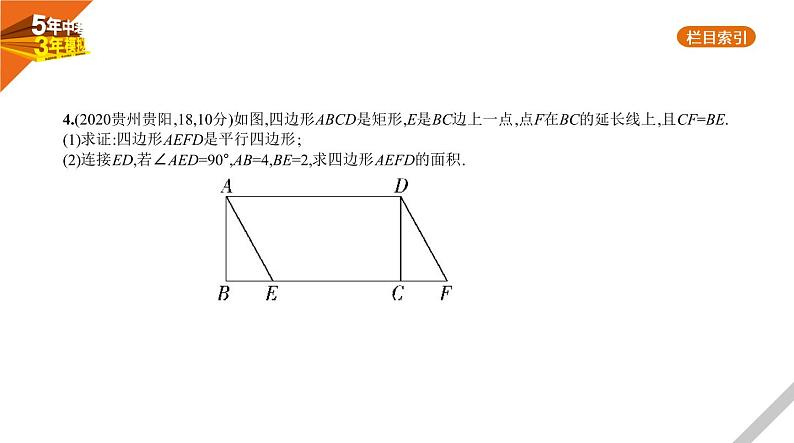
4.(2020贵州贵阳,18,10分)如图,四边形ABCD是矩形,E是BC边上一点,点F在BC的延长线上,且CF=BE.(1)求证:四边形AEFD是平行四边形;(2)连接ED,若∠AED=90°,AB=4,BE=2,求四边形AEFD的面积.
解析 (1)证明:∵四边形ABCD是矩形,∴AD∥BC,AD=BC.∵CF=BE,∴CF+EC=BE+EC,即EF=BC.∴EF=AD,∴四边形AEFD是平行四边形.(2)如图. ∵四边形ABCD是矩形,∴∠B=90°,在Rt△ABE中,AB=4,BE=2,∴由勾股定理得,EA2=16+4=20,即EA=2 .∵AD∥BC,∴∠DAE=∠AEB.
∵∠B=∠AED=90°,∴△ABE∽△DEA.∴ = ,即 = ,∴AD=10.由(1)得四边形AEFD是平行四边形,∴EF=AD=10,又AB=4,∴S▱AEFD=EF·AB=10×4=40.
1.(2020四川南充,7,4分)如图,面积为S的菱形ABCD中,点O为对角线的交点,点E是线段BC的中点,过点E 作EF⊥BD于F,EG⊥AC于G,则四边形EFOG的面积为 ( ) A. S B. S C. S D. S
答案 B ∵四边形ABCD是菱形,∴AC⊥BD,S△OBC= S,∵EF⊥BD,EG⊥AC,∴四边形EFOG是矩形,∴EF∥OC,EG∥OB,∵点E是线段BC的中点,∴EF、EG都是△OBC的中位线,∴S四边形EFOG= S△OBC= S.故选B.
2.(2020宁夏,5,3分)如图,菱形ABCD的边长为13,对角线AC=24,点E、F分别是边CD、BC的中点,连接EF 并延长与AB的延长线相交于点G,则EG= ( ) A.13 B.10 C.12 D.5
答案 B 连接BD交AC于点O.在菱形ABCD中,AC⊥BD,且OC=OA=12,在Rt△DOC中,OD= = =5,∴BD=10.又∵E、F分别是CD、BC的中点,∴EF= BD=5.易得△EFC≌△GFB,∴EF=FG,∴EG=10.
3.(2019贵州贵阳,4,3分)如图,菱形ABCD的周长是4 cm,∠ABC=60°,那么这个菱形的对角线AC的长是 ( ) A.1 cm B.2 cm C.3 cm D.4 cm
答案 A 由已知及菱形四条边都相等可知AB=BC=1 cm,因为∠ABC=60°,所以三角形ABC为等边三角 形,所以AC=AB=1 cm,故选A.
4.(2019天津,8,3分)如图,四边形ABCD为菱形,A,B两点的坐标分别是(2,0),(0,1),点C,D在坐标轴上,则菱形 ABCD的周长等于 ( )A. B.4 C.4 D.20
5.(2018新疆,9,5分)如图,点P是边长为1的菱形ABCD对角线AC上的一个动点,点M,N分别是AB,BC边上的 中点,则MP+PN的最小值是 ( )A. B.1 C. D.2
答案 B 如图,取AD的中点M',连接M'N,M'P,则有MP=M'P.MP+PN的最小值为线段M'N的长,即菱形边 长1.故选B.
6.(2020新疆,18,8分)如图,四边形ABCD是平行四边形,DE∥BF,且分别交对角线AC于点E,F,连接BE,DF.(1)求证:AE=CF;(2)若BE=DE,求证:四边形EBFD为菱形. 证明 (1)∵DE∥BF,∴∠DEF=∠BFE,∴∠AED=∠BFC(等角的补角相等),又∵四边形ABCD为平行四边形,∴AD=BC且AD∥BC,
∴∠DAE=∠BCF,在△ADE和△CBF中, ∴△ADE≌△CBF(AAS).∴AE=CF.(2)由(1)可知△ADE≌△CBF,∴DE=BF,又∵DE∥BF,∴四边形EBFD为平行四边形,又∵BE=DE,∴平行四边形EBFD为菱形(一组邻边相等的平行四边形是菱形).
思路分析 (1)由DE∥BF证出∠DEF=∠BFE,可得∠AED=∠BFC;由四边形ABCD是平行四边形可证得 AD=BC且AD∥BC,从而有∠DAE=∠BCF,利用AAS得出△ADE≌△CBF,即得AE=CF.(2)由(1)中的△ADE≌△CBF可得到DE=BF,从而证得四边形EBFD为平行四边形,结合BE=DE可证得结 论.
1.(2019甘肃兰州,12,4分)如图,边长为 的正方形ABCD的对角线AC与BD交于点O,将正方形ABCD沿直线DF折叠,点C落在对角线BD上的点E处,折痕DF交AC于点M,则OM= ( ) A. B. C. -1 D. -1
答案 D 连接EM,由折叠性质可知EM=CM,DE=DC= ,在正方形ABCD中,AC= DC=2,OC=OD= AC=1,AC⊥BD,∴EM=CM=1-OM,OE= -1.解法一:在Rt△EOM中,OM2+OE2=EM2,即OM2+ =(1-OM)2,解得OM= -1.解法二:易知∠DMO=∠FMC,且∠DOC=∠DFC=90°,∴∠ODM=∠FCM,又∵OD=OC,∠DOM=∠COE=9 0°,∴△DOM≌△COE,∴OM=OE= -1,故选D.
2.(2019内蒙古包头,11,3分)如图,在正方形ABCD中,AB=1,点E、F分别在边BC和CD上,AE=AF,∠EAF=60 °,则CF的长是 ( ) A. B. C. -1 D.
答案 C 如图,连接EF,在正方形ABCD中,AB=AD,∠B=∠D=90°.又∵AE=AF,∴Rt△ABE≌Rt△ADF, ∴BE=DF.∵BC=CD,∴CE=CF.∵∠EAF=60°,∴△AEF是等边三角形.设CE=x(0
解析 ∵四边形ABCD为正方形,∴∠BCD=90°,AB∥CD,AB=BC,∠ABE=∠CBE,又∵BE=BE,∴△ABE≌△CBE(SAS),∴∠BCE=∠BAE=56°,∴∠ECF=90°-∠BCE=34°,∵AB∥CD,∴∠EFD=∠BAE=56°,∵∠EFD=∠ECF+∠CEF,∴∠CEF=56°-34°=22°.故答案为22.
4.(2020宁夏,16,3分)2002年8月,在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾 股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图1),且大正方形 的面积是15,小正方形的面积是3,直角三角形的较短直角边长为a,较长直角边长为b.如果将四个全等的 直角三角形按图2的形式摆放,那么图2中的大正方形的面积为 .
思路分析 先根据题图1求出直角三角形的面积和大正方形的边长,然后求出题图2中的大正方形的面 积.
5.(2019内蒙古呼和浩特,15,3分)已知正方形ABCD的面积是2,E为正方形一边BC在从B到C方向的延长线 上的一点.若CE= ,连接AE,与正方形另外一边CD交于点F,连接BF并延长,与线段DE交于点G,则BG的长为 .
解析 如图,延长BG,AD交于点Q.∵正方形ABCD的面积为2,∴边长为 ,AQ∥BC,CF∥AB. ∵CE=BC= ,∴CF=DF= AB,易证△DQF≌△CBF,△DQG∽△EBG,∴DQ=BC= , = ,在Rt△ABQ中,由勾股定理得BQ= = .∵ = ,∴ = ,∴BG= .
6.(2020内蒙古呼和浩特,18,8分)如图,正方形ABCD中,G是BC边上任意一点(不与B、C重合),DE⊥AG于 点E,BF∥DE,且交AG于点F.(1)求证:AF-BF=EF;(2)四边形BFDE能否为平行四边形?如果能,请指出此时点G的位置;如果不能,请说明理由.
解析 (1)证明:由题意可知AB=AD,∠BAF+∠DAE=90°,∵DE⊥AG,∴∠DAE+∠ADE=90°,∴∠ADE=∠BAF,又∵BF∥DE,∴∠BFA=90°=∠AED,∴△ABF≌△DAE(AAS),∴BF=AE,∴AF-BF=AF-AE=EF.(2)不可能,理由:假设四边形BFDE是平行四边形,已知DE∥BF,则当DE=BF时,四边形BFDE为平行四边形,由(1)知DE=AF,∴BF=AF,即此时∠BAF=45°,此时点G与点C重合而点G不与C重合,∴∠BAF≠45°,矛盾,∴四边形BFDE不能是平行四边形.
1.(2019河北,16,2分)对于题目:“如图1,平面上,正方形内有一长为12、宽为6的矩形,它可以在正方形的 内部及边界通过移转(即平移或旋转)的方式,自由地从横放移转到竖放,求正方形边长的最小整数n.” 甲、乙、丙作了自认为边长最小的正方形,先求出该边长x,再取最小整数n. 图1
甲:如图2,思路是当x为矩形对角线长时就可移转过去;结果取n=13. 图2 图3 图4乙:如图3,思路是当x为矩形外接圆直径长时就可移转过去;结果取n=14.丙:如图4,思路是当x为矩形的长与宽之和的 倍时就可移转过去;结果取n=13.下列正确的是 ( )A.甲的思路错,他的n值对B.乙的思路和他的n值都对C.甲和丙的n值都对D.甲、乙的思路都错,而丙的思路对
答案 B 当x为矩形对角线长时,根据勾股定理得x= = >13,最小整数n应为14,所以甲的思路正确,他的n值错误;当x为矩形外接圆直径长(即矩形对角线长)时,x= >13,最小整数n应为14,所以乙的思路正确,他的n值正确;根据丙的思路,x= (6+12)=9 <13,而矩形对角线长>13,所以丙的思路错误,他的n值错误.故选B.
思路分析 分别按甲、乙、丙三人的思路求出各自x的值,根据题意确定各自所取n的值并与矩形对角 线长进行比较即可得解.
易错警示 三者思路的正误及n值的判断取决于x值不能小于矩形对角线长.
2.(2018安徽,14,5分)矩形ABCD中,AB=6,BC=8.点P在矩形ABCD的内部,点E在边BC上,满足△PBE∽△ DBC.若△APD是等腰三角形,则PE的长为 .
3.(2018北京,13,2分)如图,在矩形ABCD中,E是边AB的中点,连接DE交对角线AC于点F,若AB=4,AD=3,则 CF的长为 .
4.(2020内蒙古包头,20,3分)如图,在矩形ABCD中,BD是对角线,AE⊥BD,垂足为E,连接CE.若∠ADB=30°, 则tan∠DEC的值为 .
解析 过点C作CF⊥BD于F,如图所示, ∵四边形ABCD为矩形,∴AB=CD,∠ADC=∠BAD=90°,∴∠FDC=∠ADC-∠ADB=90°-30°=60°,∠ABD=90°-∠ADB=90°-30°=60°,设AB=CD=2x(x>0),在Rt△ABD中,BD= = = =4x,在Rt△CDF中,CF=CD·sin∠FDC=CD·sin 60°=2x· = x,DF=CD·cs∠FDC=CD·cs 60°=2x· =x,
在Rt△ABE中,BE=AB·cs∠ABE=2x· =x,∴EF=BD-BE-DF=4x-x-x=2x,在Rt△CEF中,tan∠DEC= = = .
5.(2019贵州贵阳,15,4分)如图,在矩形ABCD中,AB=4,∠DCA=30°,点F是对角线AC上的一个动点,连接 DF,以DF为斜边作∠DFE=30°的直角三角形DEF,使点E和点A位于DF两侧,点F从点A到点C的运动过程 中,点E的运动路径长是 .
解析 连接BD,交AC于点O,∵矩形ABCD中,∠DCA=30°,∴三角形AOD为等边三角形.∵AB=4,∴AD= OD=ABtan 30°= .当点F与点A重合时,点E在OD的中点E1处,DE1= OD= ;当点F与点C重合时,点E(即E2)在DC的上方.连接E1E2,易知∠E1DE2=∠ADC=90°,∠DE1E2=60°.∵∠DFE=∠DAE1=30°,∴ = = ,又∠FDE=∠ADE1=60°,∴∠FDA=∠EDE1,∴△ADF∽△E1DE,∴∠DAF=∠DE1E=60°,由此可知点E的运动轨迹为线段E1E2,∵∠E1DE2=90°,∠DE1E=60°,∴E1E2=2DE1= .
思路分析 首先确定点E的始点和终点,进而确定点E的运动轨迹,最后利用直角三角形的性质求得结果.
易错警示 本题的关键是确定点E的运动轨迹,错误得出点E的位置变化也就造成了误解.
6.(2019福建,18,8分)如图,点E,F分别在矩形ABCD的边AB,CD上,且DF=BE.求证:AF=CE. 证明 ∵四边形ABCD是矩形,∴∠D=∠B=90°,AD=CB.在△ADF和△CBE中, ∴△ADF≌△CBE,∴AF=CE.
7.(2019江西,13(2),3分)如图,四边形ABCD中,AB=CD,AD=BC,对角线AC、BD相交于点O,且OA=OD.求 证:四边形ABCD是矩形. 证明 ∵AB=CD,AD=BC,∴四边形ABCD是平行四边形.∴OA= AC,OD= BD,又∵OA=OD,∴AC=BD.∴▱ABCD是矩形.
1.(2020贵州贵阳,7,3分)菱形的两条对角线长分别是6和8,则此菱形的周长是 ( )A.5 B.20 C.24 D.32
2.(2018贵州贵阳,5,3分)如图,在菱形ABCD中,E是AC的中点,EF∥CB,交AB于点F,如果EF=3,那么菱形 ABCD的周长为 ( ) A.24 B.18 C.12 D.9
答案 A ∵E是AC的中点,∴AC=2AE.∵EF∥CB,∴ = =2,∴BC=2EF=6,∴菱形ABCD的周长为6×4=24.故选A.
3.(2020陕西,14,3分)如图,在菱形 ABCD中,AB=6,∠B=60°,点E在边AD上,且AE=2.若直线l经过点E,将该 菱形的面积平分,并与菱形的另一边交于点F,则线段EF的长为 .
解析 过A作AG⊥BC于G,过E作EH⊥BC于H,则四边形AGHE为矩形,∴AE=GH=2. 在菱形ABCD中,AB=6,∠B=60°,∴AG=ABsin B=6× =3 =EH,BG=ABcs B=6× =3.∴HC=BC-BG-GH=6-3-2=1.∵EF平分菱形ABCD的面积,∴AE=FC=2.∴FH=FC-CH=2-1=1.
在Rt△EFH中,由勾股定理可得EF= = =2 .
4.(2019浙江温州,15,5分)三个形状、大小相同的菱形按如图所示的方式摆放,已知∠AOB=∠AOE=90°, 菱形的较短对角线长为2 cm.若点C落在AH的延长线上,则△ABE的周长为 cm.
解析 过C作OA的垂线交AO的延长线于M,设菱形的较长对角线长为x cm.∵点C落在AH的延长线上,∴在△AMC中,OM=1,AM=x+1,CM= ,∴OH=OC= = ,又∠COH=∠COB+∠BOH=∠AOH+∠BOH=∠AOB=90°,∴S△ACM=S△COH+S△COM+S△OAH,∴ = + + ,即x2-4x-4=0,解得x1=2 +2,x2=-2 +2(舍),∴△ABE的周长=AB+AE+OB+OE
= x+ x+x+x=(2+2 )x=(2+2 )(2 +2)=(12+8 )cm.
5.(2018辽宁沈阳,18,8分)如图,在菱形ABCD中,对角线AC与BD交于点O,过点C作BD的平行线,过点D作 AC的平行线,两直线相交于点E.(1)求证:四边形OCED是矩形;(2)若CE=1,DE=2,则菱形ABCD的面积是 .
解析 (1)证明:∵四边形ABCD为菱形,∴AC⊥BD,∴∠COD=90°.∵CE∥OD,DE∥OC,∴四边形OCED是平行四边形.∵∠COD=90°,∴平行四边形OCED是矩形.(2)4.由四边形OCED是矩形得OC=DE=2,OD=CE=1,∴S菱形ABCD=4S△OCD=4× ×2×1=4.
6.(2019甘肃兰州,22,7分)如图,AC=8,分别以A,C为圆心,以长度5为半径作弧,两条弧分别相交于点B和D, 依次连接A,B,C,D,连接BD交AC于点O.(1)判断四边形ABCD的形状并说明理由;(2)求BD的长.
解析 (1)由题可知,BD垂直平分AC,且AB=BC=CD=AD=5,∴四边形ABCD为菱形.(2)∵AC=8,BD⊥AC且BD平分AC,∴OA=OC=4,∴在Rt△AOB中,OB= = =3,∴BD=2OB=2×3=6,∴BD的长为6.
7.(2019北京,20,5分)如图,在菱形ABCD中,AC为对角线,点E,F分别在AB,AD上,BE=DF,连接EF.(1)求证:AC⊥EF;(2)延长EF交CD的延长线于点G,连接BD交AC于点O.若BD=4,tan G= ,求AO的长.
解析 (1)证明:∵四边形ABCD为菱形,∴AB=AD,AC平分∠BAD.∵BE=DF,∴AE=AF.∴AC⊥EF.(2)∵四边形ABCD为菱形,∴AO=OC,OD= BD,AC⊥BD.∵EF⊥AC,∴BD∥EG.∴∠G=∠BDC.∵BD=4,∴OD=2.在Rt△COD中,由tan∠CDO=tan G= ,可得OC=1.
8.(2020云南,22,9分)如图,四边形ABCD是菱形,点H为对角线AC的中点,点E在AB的延长线上,CE⊥AB,垂 足为E,点F在AD的延长线上,CF⊥AD,垂足为F.(1)若∠BAD=60°,求证:四边形CEHF是菱形;(2)若CE=4,△ACE的面积为16,求菱形ABCD的面积.
解析 (1)证明:∵在菱形ABCD中,∠BAD=60°,∴∠BAC=30°. (1分)∵CE⊥AB,垂足为E,H为对角线AC的中点,∴CE= AC=CH,∠ECH=90°-∠EAC=60°.∴△CEH是等边三角形,∴CE=CH=EH.同理可证CF=CH=FH. (3分)∴CE=EH=FH=CF,∴四边形CEHF是菱形. (4分)(2)∵CE=4,S△ACE=16,CE⊥AB,垂足为E,∴ AE·CE=16,解得AE=8. (6分)∵四边形ABCD是菱形,∴AB=BC.设AB=BC=x,则BE=8-x.由BC2=CE2+BE2,即x2=42+(8-x)2,
解得x=5,即AB=5. (8分)∴S△ABC= AB·CE= ×5×4=10,∴S菱形ABCD=2S△ABC=20. (9分)
9.(2018北京,21,5分)如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过 点C作CE⊥AB交AB的延长线于点E,连接OE.(1)求证:四边形ABCD是菱形;(2)若AB= ,BD=2,求OE的长.
解析 (1)证明:∵AB∥CD,∴∠OAB=∠DCA.∵AC平分∠BAD,∴∠OAB=∠DAC,∴∠DCA=∠DAC,∴CD=AD.又∵AB=AD,∴AB=CD,∴四边形ABCD为平行四边形.又∵CD=AD=AB,∴四边形ABCD为菱形.(2)∵四边形ABCD为菱形,∴OA=OC,BD⊥AC.∵CE⊥AE,∴OE=AO=OC.∵BD=2,∴OB= BD=1.在Rt△AOB中,AB= ,OB=1,∴OA= =2,∴OE=2.
1.(2019新疆,9,5分)如图,正方形ABCD的边长为2,点E是BC的中点,AE与BD交于点P,F是CD上一点,连接 AF分别交BD,DE于点M,N,且AF⊥DE,连接PN,则以下结论中:①S△ABM=4S△FDM;②PN= ;③tan∠EAF= ;④△PMN∽△DPE.正确的是 ( ) A.①②③ B.①②④ C.①③④ D.②③④
答案 A ∵正方形ABCD的边长为2,点E是BC的中点,∴AB=BC=CD=AD=2,∠ABC=∠C=∠ADF=90°,CE=BE=1.∵AF⊥DE,∴易证△ADF≌△DCE,∴DF=CE=1.∵AB∥DF,∴△ABM∽△FDM,∴ = =4,∴S△ABM=4S△FDM ,故①正确.由勾股定理可知:AF=DE=AE= = ,∵ ·AD·DF= ·AF·DN,∴DN= ,∴EN= ,AN= = ,∴tan∠EAF= = ,故③正确.
过点P作PH⊥AN于点H. ∵BE∥AD,∴ = =2,∴PA= ,∵sin∠EAF= = ,
∴PH=PA·sin∠EAF= ,∵PH∥EN,∴ = = ,∴AH= × = ,HN= ,∴PN= = ,故②正确.∵PN≠DN,∴∠DPN≠∠PDE,∴△PMN与△DPE不相似,故④错误.故选A.
2.(2019广东,10,3分)如图,正方形ABCD的边长为4,延长CB至E使EB=2,以EB为边在上方作正方形EFGB, 延长FG交DC于M,连接AM、AF,H为AD的中点,连接FH分别与AB、AM交于点N、K,则下列结论:①△ ANH≌△GNF;②∠AFN=∠HFG;③FN=2NK;④S△AFN∶S△ADM=1∶4,其中正确的结论有 ( ) A.1个 B.2个 C.3个 D.4个
答案 C 因为正方形ABCD的边长为4,正方形EFGB的边长为2,H为AD的中点,所以FG=AH=2,∠HAN= ∠FGN=90°,AD∥FM,所以∠AHN=∠GFN,所以△ANH≌△GNF,故①正确.因为在Rt△AFG中,AF= =2 ,而AH=2,所以∠AHF≠∠AFH,则∠AFN≠∠HFG,故②错误.由AD∥FM,可知△AHK∽△MFK,所以HK∶FK=AH∶FM=2∶6=1∶3.因为△ANH≌△GNF,所以FN=HN,所以HF=4HK=2FN,所以 HK=NK,所以FN=2NK,故③正确.易求得S△AFN= ×1×2=1,S△ADM= ×2×4=4,所以S△AFN∶S△ADM=1∶4,故④正确.综上所述,正确的结论有3个,故选C.
方法总结 证明三角形全等,从已知中找边和角相等;在一个三角形中看两角是否相等,可以证明相对两 边是否相等;一个边是另一个边的倍数关系常要联系到相似.
3.(2019安徽,10,4分)如图,在正方形ABCD中,点E,F将对角线AC三等分,且AC=12.点P在正方形的边上,则 满足PE+PF=9的点P的个数是( ) A.0 B.4 C.6 D.8
答案 D 如图,作E,F关于AD的对称点E1,F1,连接E1F,EF1,交AD于H点,连接EE1,FF1,过点F作FO⊥EE1,交 E1E的延长线于点O,当P点在H点时,PE+PF取得最小值,由已知得AE=EF=CF=4,∵四边形ABCD是正方 形,∴易求OE=EM=ME1=2 ,∴OF=OE=2 ,OE1=6 ,由勾股定理可得EF1=E1F= = <9,∴在AH和HD上各存在一点P,使得PE+PF=9,同理在AB、BC、CD上各存在2个这样的P点,∴一共有 8个这样的P点,故选D.
思路分析 因为正方形具有对称性,所以只需找出正方形一条边上满足条件的个数,然后乘4即可,由E,F 为定点且为AC的三等分点,分别作E,F关于AD的对称点,这样可求出PE+PF的最小值为 <9,从而可得AD上满足条件的点有两个,问题解决.
4.(2017内蒙古呼和浩特,9,3分)如图,四边形ABCD是边长为1的正方形,E,F为BD所在直线上的两点.若AE = ,∠EAF=135°,则以下结论正确的是 ( ) A.DE=1B.tan∠AFO= C.AF= D.四边形AFCE的面积为
答案 C ∵四边形ABCD是边长为1的正方形,∴对角线AC、BD互相垂直平分且相等,∴AO=OD= ,在Rt△AOE中,OE= = ,∴DE=OE-OD= ,∴A选项错误;易知∠ADO=45°,∴∠ADE=135°,∴∠ADE=∠EAF,又∠AED=∠FEA,∴△DAE∽△AFE,∴ = = = ,∴AF= ,∴C选项正确;在Rt△AOF中,OF= = ,∴tan∠AFO= = ,∴B选项错误;∵EF=OF+OE= ,∴四边形AFCE的面积= EF·AC= × × = ,∴D选项错误.故选C.
5.(2019北京,14,2分)把图1中的菱形沿对角线分成四个全等的直角三角形,将这四个直角三角形分别拼 成如图2,图3所示的正方形,则图1中菱形的面积为 .
6.(2019江西,8,3分)我国古代数学名著《孙子算经》有估算方法:“方五,邪(通“斜”)七.见方求邪,七之, 五而一.”译文为:如果正方形的边长为五,则它的对角线长为七.已知正方形的边长,求对角线长,则先将 边长乘七再除以五.若正方形的边长为1,由勾股定理得对角线长为 ,依据《孙子算经》的方法,则它的对角线的长是 .
7.(2018内蒙古呼和浩特,16,3分)如图,已知正方形ABCD,点M是边BA延长线上的动点(不与点A重合),且 AM
解题关键 解决本题的关键是要借助中点发现辅助圆.
8.(2019北京,16,2分)在矩形ABCD中,M,N,P,Q分别为边AB,BC,CD,DA上的点(不与端点重合).对于任意矩形ABCD,下面四个结论中,①存在无数个四边形MNPQ是平行四边形;②存在无数个四边形MNPQ是矩形;③存在无数个四边形MNPQ是菱形;④至少存在一个四边形MNPQ是正方形.所有正确结论的序号是 .
解析 如图,由于是任意矩形,不妨设AD>AB,取矩形的中心O,在AB边上任取一点M,连接MO并延长交 CD于点P,在BC边上任取一点N,连接NO并延长交AD于点Q,则四边形MNPQ是平行四边形,因为是任取, 所以存在无数个四边形MNPQ是平行四边形,①正确.可以构造NQ总垂直于MP,所以存在无数个四边形 MNPQ是菱形,③正确. 以点O为圆心,OM长为半径 作圆,当MO= AD时,☉O与矩形有六个交点,取AD与BC边上关于O点对称的两个交点分别为Q,N,取AB,DC边上的交点分别为M,P(如图1),顺次连接这四个交点,则 四边形MNPQ为矩形;当 AD
易证△AMQ≌△DQP,∴AM=QD,AQ=PD,易证△BOM≌△DOP,∴PD=BM,∴AQ=BM,∴AB=AM+BM=QD+AQ=AD,∴四边形ABCD是正方形,与任意矩形ABCD矛盾,所以④错误. 所以正确结论的序号是①②③.
思路分析 本题需要借助(特殊)平行四边形与对角线相关的判定方法来解决.
解题关键 解决本题的关键是用对角线的关系判定四边形的形状——画图时一定要关注AC,BD的交点O.
9.(2019山东潍坊,22,10分)如图,正方形ABCD的边CD在正方形ECGF的边CE上,连接DG,过点A作AH∥ DG,交BG于点H.连接HF,AF,其中AF交EC于点M.(1)求证:△AHF为等腰直角三角形;(2)若AB=3,EC=5,求EM的长.
解析 (1)证明:∵AD∥CG,AH∥DG,∴四边形ADGH为平行四边形, (1分)∴AD=HG.∵AD=BC,∴BC=HG,∴BC+CH=GH+HC, (2分)即BH=CG,∴GF=BH. (3分)在△ABH和△HGF中,AB=HG,∠B=∠HGF,BH=GF,∴△ABH≌△HGF, (4分)∴∠BAH=∠GHF,AH=HF.∵∠BAH+∠BHA=90°,∴∠GHF+∠BHA=90°,∴∠AHF=90°, (5分)∴△AHF为等腰直角三角形. (6分)(2)∵AB=3,EC=5,∴AD=CD=3,CE=EF=5,
∴DE=2. (7分)∵AD∥EF,∴ = = , (9分)∴EM= DE= . (10分)
一题多解 (1)∵四边形ABCD,四边形ECGF都是正方形,∴DA∥BC,AD=CD,FG=CG,∠B=∠CGF=90°.又∵AH∥DG,∴四边形AHGD是平行四边形,∴AH=DG,AD=HG=CD.∵∠DCG=∠HGF=90°,FG=CG,∴△DCG≌△HGF(SAS),∴DG=HF,∠HFG=∠DGC,∴AH=HF.∵∠HGD+∠DGF=90°,∴∠HFG+∠DGF=90°,∴DG⊥HF.∵AH∥DG,∴AH⊥HF,∴△AHF为等腰直角三角形.
10.(2020山西,22,12分)问题情境:如图①,点E为正方形ABCD内一点,∠AEB=90°,将Rt△ABE绕点B按顺时针方向旋转90°,得到△CBE'(点A 的对应点为点C).延长AE交CE'于点F,连接DE.猜想证明:(1)试判断四边形BE'FE的形状,并说明理由;(2)如图②,若DA=DE,请猜想线段CF与FE'的数量关系并加以证明;解决问题:(3)如图①,若AB=15,CF=3,请直接写出DE的长.
解析 (1)四边形BE'FE是正方形. (1分)理由:由旋转可知∠E'=∠AEB=90°, (2分)∠EBE'=90°. (3分)又∵∠AEB+∠FEB=180°,∠AEB=90°,∴∠FEB=90°.∴四边形BE'FE是矩形. (4分)由旋转可知,BE'=BE.∴四边形BE'FE是正方形. (5分)(2)CF=FE'.证明:如图,过点D作DH⊥AE,垂足为H, (6分)
则∠DHA=90°,∠1+∠3=90°,∵DA=DE,∴AH= AE. (7分)∵四边形ABCD是正方形,∴AB=DA,∠DAB=90°.∴∠1+∠2=90°.∴∠2=∠3.∵∠AEB=∠DHA=90°,∴△AEB≌△DHA. (8分)∴AH=BE.由(1)知四边形BE'FE是正方形,
∴BE=E'F.∴AH=E'F. (9分)由旋转可得CE'=AE,∴FE'= CE'.∴CF=FE'. (10分)
(3)3 . (12分)详解:由(1)知四边形BE'FE是正方形,∴FE'=BE,由旋转得CE'=AE,∵CF=3,∴BE=FE'=AE-3,在Rt△ABE中, AE2+BE2=AB2,即AE2+(AE-3)2=152,解得AE=12或-9(舍),作DH⊥AE于H点,∵∠DAH+∠ADH=∠DAH+∠EAB=90°,∴∠ADH=∠EAB,又∠AHD=∠AEB=90°,∴△DAH∽△ABE,∴ = =1,∴DH=AE=12,∴AH= = =9,∴HE=3,∴DE= = =3 .
思路分析 (1)根据旋转先证四边形BE'FE是矩形,再由旋转得BE'=BE,问题得解;(2)作DH⊥AE于点H,由 等腰三角形“三线合一”可得点H为AE的中点,根据四边形ABCD是正方形可证△AEB≌△DHA,可得 AH=BE,再根据(1)的结论及旋转可证;(3)由(1)可知BE=AE-3,在Rt△ABE中,AE2+BE2=AB2,解得AE=12,再 作DH⊥AE于H点,易证△DAH∽△ABE,从而求出DH、AH,最后在Rt△DHE中求出DE.
11.(2020四川南充,24,10分)如图,边长为1的正方形ABCD中,点K在AD上,连接BK,过点A,C作BK的垂线,垂 足分别为M,N,点O是正方形ABCD的中心,连接OM,ON.(1)求证:AM=BN;(2)请判定△OMN的形状,并说明理由;(3)若点K在线段AD上运动(不包括端点),设AK=x,△OMN的面积为y,求y关于x的函数关系式(写出x的范 围);若点K在射线AD上运动,且△OMN的面积为 ,请直接写出AK的长.
解析 (1)证明:∵AM⊥BM,CN⊥BN,∴∠AMB=∠BNC=90°.又∵∠ABC=90°,∴∠MAB+∠MBA=90°,∠NBC+∠MBA=90°,∴∠MAB=∠NBC. (1分)又AB=BC,∴△AMB≌△BNC,∴AM=BN. (2分)(2)△OMN是等腰直角三角形. (3分)理由如下:连接OB,∵O为正方形ABCD的中心, ∴∠MAB-∠OAB=∠NBC-∠OBC,即∠MAO=∠OBN. (4分)∵OA=OB,AM=BN,∴△AMO≌△BNO,∴OM=ON,∠AOM=∠BON. (5分)
∵∠AOB=∠AON+∠BON=90°,∴∠MON=90°.∴△OMN是等腰直角三角形. (6分)(3)在Rt△ABK中,BK= = .由BK·AM=AB·AK,得BN=AM= = . (7分)由AK2=KM·BK,得KM= = . (8分)∴MN=BK-BN-KM= - - = .∴S△OMN= MN2= .即y= (0
1.(2020天津部分区一模,9)如图,矩形ABCD中,连接AC,延长BC至点E,使BE=AC,连接DE.若∠BAC=40°,则 ∠E的度数是 ( ) A.65° B.60° C.50° D.40°
答案 A 如图,连接BD,交AC于点O, ∵矩形ABCD中,∠BAC=40°,OA=OB,∴∠ABD=40°,∴∠DBE=90°-40°=50°.∵AC=BD,AC=BE,∴BD=BE,∴△BDE中,∠E= (180°-∠DBE)=65°,故选A.
2.(2020天津河北3月模拟,10)如图,在矩形ABCD中,AB=4,BC=6,过对角线交点O作EF⊥AC交AD于点E,交 BC于点F,则DE的长是 ( ) A.1 B. C.2 D.
答案 D 连接CE,如图所示, ∵四边形ABCD是矩形,∴∠ADC=90°,CD=AB=4,AD=BC=6,OA=OC.∵EF⊥AC,∴AE=CE,设DE=x,则CE=AE=6-x,在Rt△CDE中,由勾股定理得x2+42=(6-x)2,解得x= ,即DE= .故选D.
3.(2019上海浦东新区二模,6)已知在四边形ABCD中,AD∥BC,对角线AC与BD相交于点O,AO=CO,添加 下列一个条件后,就能判定这个四边形是菱形的为 ( )A.BO=DO B.AB=BCC.AB=CD D.AB∥CD
答案 B ∵AD∥BC,∴∠ADO=∠CBO.在△ADO与△CBO中, ∴△ADO≌△CBO(AAS),∴AD=CB.又∵AD∥BC,∴四边形ABCD是平行四边形.∵AB=BC,∴四边形ABCD是菱形.故B正确.
4.(2019四川眉山东坡一模,10)如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB, 垂足为F,则EF的长为 ( ) A.1 B. C.4-2 D.3 -4
答案 C 在正方形ABCD中,∠ABD=∠ADB=45°,∵∠DAE=90°-∠BAE=67.5°,∴在△ADE中,∠AED=180°-∠ADB-∠DAE=67.5°,∴∠DAE=∠AED,∴AD=DE=4.∵正方形的边长为4,∴BD=4 ,∴BE=BD-DE=4 -4.∵EF⊥AB,∠ABD=45°,∴△BEF是等腰直角三角形,∴EF= BE= ×(4 -4)=4-2 .故选C.
5.(2018天津南开一模,11)如图,将菱形纸片ABCD折叠,使点A恰好落在菱形的对称中心O处,折痕为EF.若 菱形ABCD的边长为2 cm,∠A=120°,则EF= ( ) A.2 cm B.2 cm C. cm D.4 cm
答案 C 连接AO,交EF于点H,连接BD. 依题意知EF垂直平分AO,AO垂直平分BD,∴EF∥BD,AH=HO,∴点E、F分别是AB、AD的中点,则EF=2EH.在△AEF中,AE=AF=1 cm,又∠EAF=120°,∴∠AEH=30°,
∴EH=EA·cs 30°= cm.∴EF=2EH= cm.故选C.
二、填空题(每小题3分,共12分)6.(2019四川成都武侯模拟,14)如图,菱形ABCD的对角线AC、BD相交于点O,tan∠DAC= ,则∠DAB的度数为 .
7.(2020湖北武汉4月调考,14)如图,在菱形ABCD中,过点A作AH⊥BC,分别交BD,BC于点E,H,F为ED的中 点,∠BAF=120°,则∠C的度数为 .
解析 设∠CBD=x,∵四边形ABCD为菱形,∴AD∥BC,∠ABD=∠CBD=x,∴∠ADB=∠CBD=x.∵AH⊥BC,AD∥BC,∴∠DAH=∠AHB=90°.∵F为ED的中点,∴AF=FD,∴∠FAD=∠ADB=x,∴∠AFB=2x.在△ABF中,∠AFB+∠BAF+∠ABF=180°,即2x+120°+x=180°,解得x=20°,∴∠BAD=120°+x=140°,又∵四边形ABCD为菱形,∴∠C=∠BAD=140°.
8.(2020天津河西3月模拟,17)如图,已知点E在正方形ABCD的边AB上,以BE为边在正方形ABCD外部作正 方形BEFG,连接DF,M、N分别是DC、DF的中点,连接MN,若AB=9,BE=6,则MN的长为 .
解析 如图,连接CF, ∵正方形ABCD和正方形BEFG中,AB=9,BE=6,∴GF=GB=6,BC=9,∴GC=GB+BC=6+9=15,∴CF= = =3 .∵M、N分别是DC、DF的中点,∴MN= = .
9.(2019天津和平一模,17)如图,正方形ABCD的边长为2,正方形AEFG的边长为2 ,点B在线段DG上,则BE的长为 .
∴△DAG≌△BAE(SAS).∴DG=BE,∠DGA=∠BEA.∵∠AEO+∠AOE=90°,∠BOG=∠AOE,∴∠BGO+∠GOB=90°,即∠GBE=90°.设BE=x(x>0),则BG=x-2 ,又知EG=4,在Rt△BGE中,利用勾股定理可得x2+(x-2 )2=42,解得x= + .∴BE= + .
三、解答题(共33分)10.(2020江西南昌一模,15)如图,在矩形ABCD中,E、F分别是BC,AD边上的点,且AE=CF,若AC⊥EF,试判 断四边形AECF的形状,并说明理由.
解析 四边形AECF是菱形,理由如下:∵四边形ABCD是矩形,∴∠B=∠D=90°,AB=CD,AD=BC,AD∥BC.在Rt△ABE和Rt△CDF中, ∴Rt△ABE≌Rt△CDF(HL),∴BE=DF.∵BC=AD,∴BC-BE=AD-DF,即CE=AF,又∵CE∥AF,∴四边形AECF是平行四边形,又∵AC⊥EF,∴四边形AECF是菱形.
11.(2020海南琼海一模,19)如图,已知在四边形ABCD中,AD∥BC,AB⊥AD,BC=CD,BE⊥CD,垂足为点E, 点F在BD上,连接AF、EF.(1)求证:AD=ED;(2)如果AF∥CD,判断四边形ADEF是什么特殊四边形,证明你的结论.
解析 (1)证明:∵BC=CD,∴∠CDB=∠CBD.∵AD∥BC,∴∠ADB=∠CBD.∴∠ADB=∠CDB.∵AB⊥AD,BE⊥CD,∴∠BAD=∠BED=90°,又∵BD=BD,∴△ABD≌△EBD,∴AD=ED.(2)四边形ADEF是菱形.证明:∵AF∥CD,∴∠AFD=∠EDF.又∵∠EDF=∠ADF,∴∠AFD=∠ADF,∴AF=AD.又∵AD=ED,∴AF=DE.∴四边形ADEF是平行四边形,又∵AD=ED,∴四边形ADEF是菱形.
12.(2019甘肃定西一诊,24)如图,在△ABC中,点F是BC的中点,点E是线段AB的延长线上的动点,连接EF, 过点C作AB的平行线CD,与线段EF的延长线交于点D,连接CE、BD.(1)求证:四边形DBEC是平行四边形;(2)若∠ABC=120°,AB=BC=4,则在点E的运动过程中:①当BE= 时,四边形BECD是矩形,试说明理由;②当BE= 时,四边形BECD是菱形.
解析 (1)证明:∵AB∥CD,∴∠CDF=∠FEB,∠DCF=∠EBF.∵点F是BC的中点,∴BF=CF.在△DCF和△EBF中, ∴△DCF≌△EBF(AAS),∴DC=BE.又DC∥BE,∴四边形BECD是平行四边形.(2)①2.理由如下:当四边形BECD是矩形时,∠CEB=90°.∵∠ABC=120°,∴∠CBE=60°,∴∠ECB=30°,∴BE= BC=2.②4.详解:∵四边形BECD是菱形,∴BE=EC,∵∠ABC=120°,∴∠CBE=60°,∴△CBE是等边三角形,∴BE=BC=4.
B组 2018—2020年模拟·提升题组时间:50分钟 分值:65分一、选择题(每小题3分,共15分)
1.(2020辽宁大连金州一模,9)如图,将矩形纸片ABCD折叠,使点B落在AD上点F处,折痕为EC,若AB=3,BC =5,则AE的长为 ( ) A. B.1 C. D.
答案 C 由折叠知CF=BC=5,EF=BE.∵CD=AB=3,∠D=90°,∴DF= =4,∴AF=5-4=1.设AE=x,则BE=EF=3-x,∵∠A=90°,∴AE2+AF2=EF2,即x2+12=(3-x)2,解得x= ,∴AE= .故选C.
2.(2020海南琼海一模,5)如图,在矩形ABCD中,AD=2AB,点M、N分别在边AD、BC上,连接BM、DN.若四 边形MBND是菱形,则 等于 ( ) A. B. C. D.
答案 C ∵四边形MBND是菱形,∴MD=MB.∵四边形ABCD是矩形,∴∠A=90°.设AB=x,AM=y(x、y均为正数),则MB=2x-y.在Rt△ABM中,AB2+AM2=BM2,即x2+y2=(2x-y)2,解得x= y,∴MD=MB=2x-y= y,∴ = = .故选C.
3.(2019陕西宝鸡陈仓一模,8)如图,在矩形ABCD中,AD=10,AB=6,E为BC上一点,ED平分∠AEC,则CE的长 为 ( ) A.1 B.2 C.3 D.4
4.(2020甘肃兰州一诊,12)如图,在正方形ABCD中,点E,F分别为AB,AD的中点,CE,BF相交于点G,AB=2,则 CG= ( ) A. B. C. D.
答案 D 在正方形ABCD中,BC=AB=2,∠A=∠EBC=90°,∵点E,F分别为AB,AD的中点,∴AF=BE=1.在△AFB与△BEC中, ∴△AFB≌△BEC,∴∠FBA=∠ECB.∵∠ECB+∠BEC=90°,∴∠FBA+∠BEC=90°,∴∠EGB=90°.∵tan∠ECB= = = ,∴设BG=x,CG=2x,x>0,由勾股定理可知x2+4x2=4,解得x= (舍负),∴CG= ,故选D.
5.(2019天津红桥一模,11)如图,在正方形ABCD中,E为AD的中点,P为AB上的一个动点,若AB=2,则PE+PC 的最小值为 ( ) A.1+2 B.2 C.2+ D.
答案 D 作点C关于直线AB的对称点Q,连接EQ交AB于P,则此时PE+PC的值最小,PE+PC的最小值为 EQ的长.过E作EF⊥BC于F,则四边形ABFE是矩形,∴EF=AB=2,BF=AE= AD=1,∴QF=3,∴EQ= = = ,故选D.
二、填空题(每小题3分,共9分)6.(2020江西南昌二模,10)如图,在菱形ABCD中,∠BAD=45°,DE是AB边上的高,BE=1,则菱形的面积为 .
解析 设AB=x,∵四边形ABCD是菱形,∴AD=AB=x.∵∠BAD=45°,DE⊥AB,∴∠BAD=∠ADE=45°,∴AE=ED=x-1,在Rt△ADE中,由勾股定理得AD2=AE2+DE2,即x2=(x-1)2+(x-1)2,∴x=2+ 或x=2- (舍去),∴AD=AB=2+ ,∴DE= +1,∴菱形的面积=AB·DE=(2+ )×( +1)=4+3 .
7.(2019湖北武汉东西湖区模拟,14)如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折 叠,使点B落在矩形内的点F处,连接CF,则CF的长为 .
解析 连接BF,设BF与AE交于点H.∵BC=6,点E为BC的中点,∴BE=3.又∵AB=4,∠ABE=90°,∴AE= =5,易知BH⊥AE,∴BH= ,则BF= .∵FE=BE=EC,∴∠BFC=90°,根据勾股定理得,CF= = = .
8.(2019山西大同二模,15)如图,在正方形ABCD中,F是AD的中点,E是CD上一点,∠FBE=45°,则tan∠FEB 的值是 .
解析 ∵四边形ABCD为正方形,∴BA=BC,∠ABC=90°,把△BAF绕点B顺时针旋转90°得到△BCG,如图, ∴∠BCG=∠BAF=90°,∠FBG=∠ABC=90°,AF=CG,BG=BF.又∵∠BCE=90°,∴点G、C、E共线.∵∠EBF=45°,∴∠GBE=45°.在△BEF和△BEG中,
∴△BEF≌△BEG(SAS),∴∠FEB=∠GEB.设正方形的边长为2a,CE=x,则AF=CG=DF=a,DE=2a-x,EF=EG=x+a,在Rt△DEF中,∵DF2+DE2=EF2,∴a2+(2a-x)2=(x+a)2,解得x= a.在Rt△BCE中,tan∠CEB= = =3,∴tan∠FEB=3.
三、解答题(共41分)9.(2020辽宁鞍山铁东一模,21)在菱形ABCD中,点P是BC边上一点,连接AP,点E,F是AP上的两点,连接DE, BF,使得∠AED=∠ABC,∠ABF=∠BPF.求证:(1)△ABF≌△DAE;(2)DE=BF+EF.
证明 (1)∵四边形ABCD是菱形,∴AB=AD,AD∥BC,∴∠BPA=∠DAE.∵∠ABC=∠AED,∴∠BAF=∠ADE.∵∠ABF=∠BPF,∠BPA=∠DAE,∴∠ABF=∠DAE,又∵AB=DA,∴△ABF≌△DAE(ASA).(2)∵△ABF≌△DAE,∴AE=BF,DE=AF.∵AF=AE+EF=BF+EF,∴DE=BF+EF.
10.(2020甘肃兰州一诊,27)如图,在▱ABCD中,对角线AC,BD相交于点O,以AC为斜边的等腰直角三角形 AEC的边CE与AD交于点F,连接OE,使得OE=OD.在AD上截取AH=CD,连接EH,ED.(1)判断四边形ABCD的形状,并说明理由;(2)若AB=1,BC=3,求EH的长.
解析 (1)四边形ABCD是矩形,理由如下:∵四边形ABCD是平行四边形,∴OA=OC= AC,OB=OD= BD.∵△AEC是等腰直角三角形,∴OE⊥AC,OE= AC=OA.∵OE=OD,∴OA=OD,∴AC=BD,∴平行四边形ABCD是矩形.(2)∵平行四边形ABCD是矩形,∴AD=BC=3,∠ADC=90°,CD=AB=1.∵AH=CD,∴AH=1.∵∠AEC=∠ADC=90°,∴∠DCF+∠DFC=∠EAF+∠AFE=90°.∵∠AFE=∠DFC,∴∠DCF=∠EAF.
在△AEH和△CED中, ∴△AEH≌△CED(SAS),∴EH=ED,∠AEH=∠DEC.∵∠AEH+∠HEC=∠AEC=90°,∴∠CED+∠HEC=∠HED=90°,∴EH2+ED2=DH2,∴2EH2=DH2,∴EH= DH= (AD-AH)= ×(3-1)= .
11.(2019贵州毕节3月模拟,24)已知:如图,在菱形ABCD中,点E,O,F分别为AB,AC,AD的中点,连接CE,CF, OE,OF.(1)求证:△BCE≌△DCF;(2)当AB与BC满足什么关系时,四边形AEOF是正方形?请说明理由.
解析 (1)证明:∵四边形ABCD是菱形,∴∠B=∠D,AB=BC=DC=AD.∵点E,O,F分别为AB,AC,AD的中点,∴AE=BE=DF=AF,OF= DC,OE= BC,OE∥BC.在△BCE和△DCF中, ∴△BCE≌△DCF(SAS).(2)当AB⊥BC时,四边形AEOF是正方形,理由如下:由(1)得AE=OE=OF=AF,∴四边形AEOF是菱形.∵AB⊥BC,OE∥BC,∴OE⊥AB,∴∠AEO=90°,∴菱形AEOF是正方形.
12.(2019云南昆明模拟,21)如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE= AC,连接AE交OD于点F,连接OE.(1)求证:OE=AB;(2)若菱形ABCD的边长为2,∠ABC=60°,求AE的长.
解析 (1)证明:连接EC. ∵四边形ABCD是菱形,∴OA=OC= AC,AD=AB.∵DE∥AC且DE= AC,∴DE=OA=OC,∴四边形OADE、四边形OCED都是平行四边形,∴OE=AD,∴OE=AB.(2)∵AC⊥BD,∴平行四边形OCED是矩形,
∴∠OCE=90°.∵在菱形ABCD中,∠ABC=60°,∴△ABC为等边三角形,∴AC=AB=2,∴AO= AC=1,∴在矩形OCED中,CE=OD= = .∴在Rt△ACE中,AE= = .
一、选择题(每小题5分,共25分)
1.(2020北京,4)下列图形中,既是中心对称图形也是轴对称图形的是 ( )
答案 D 选项A不是中心对称图形,是轴对称图形;选项B既不是中心对称图形也不是轴对称图形;选项 C是中心对称图形,不是轴对称图形;选项D既是中心对称图形也是轴对称图形.故选D.
2.(2019内蒙古鄂尔多斯,7)如图,在▱ABCD中,∠BDC=47°42‘,依据尺规作图的痕迹,计算α的度数是 ( ) A.67°29' B.67°9' C.66°29' D.66°9'
答案 D 如图.∵四边形ABCD为平行四边形,∴AB∥CD,∴∠ABD=∠BDC=47°42'.由尺规作图的作法得EF垂直平分线段BD,BE平分∠ABD,∴EF⊥BD,∠ABE=∠DBE= ∠ABD=23°51'.∵∠BEF+∠EBD=90°,∴∠BEF=90°-23°51°=66°9',∴α的度数是66°9'.故选D.
3.(2019湖南岳阳,7)下列命题是假命题的是 ( )A.平行四边形既是轴对称图形,又是中心对称图形B.同角(或等角)的余角相等C.线段垂直平分线上的点到线段两端的距离相等D.正方形的对角线相等,且互相垂直平分
答案 A 平行四边形是中心对称图形,但不是轴对称图形,故选项A中的命题是假命题.“同角(或等角) 的余角相等”是真命题,“线段垂直平分线上的点到线段两端的距离相等”是真命题,“正方形的对角 线相等,且互相垂直平分”是真命题.故选A.
4.(2020湖南长沙,10)如图,一块直角三角板的60°角的顶点A与直角顶点C分别在两平行线FD、GH上,斜 边AB平分∠CAD,交直线GH于点E,则∠ECB的大小为( ) A.60° B.45° C.30° D.25°
答案 C ∵AB平分∠CAD,∠CAB=60°,∴∠DAE=60°,∵FD∥GH,∴∠ACE+∠CAD=180°,∴∠ACE=180°-∠CAB-∠DAE=60°,∵∠ACB=90°,∴∠ECB=90°-∠ACE=30°.
5.(2020浙江温州,10)如图,在Rt△ABC中,∠ACB=90°,以其三边为边向外作正方形,过点C作CR⊥FG于点 R,再过点C作PQ⊥CR分别交边DE,BH于点P,Q.若QH=2PE,PQ=15,则CR的长为 ( ) A.14 B.15 C.8 D.6
答案 A 如图,连接EC,CH,设AB交CR于点J, ∵四边形ACDE和四边形BCIH是正方形,∴∠ACE=∠BCH=45°,∠ACD=90°,∠BCI=90°,∴∠ACB+∠BCI=180°,∠ACE+∠BCH+∠ACB=180°,∴A,C,I共线,E,C,H共线.易知DE∥AI∥BH,∴∠CEP=∠CHQ,又∵∠PCE=∠QCH,∴△ECP∽△HCQ,∴ = = = .
∵PQ=15,PQ=PC+CQ,∴PC=5,CQ=10.∵EC∶CH=1∶2,∴AC∶BC=1∶2,设AC=a,BC=2a,a>0,∵CR⊥PQ,CR⊥FG,∴PQ∥FG.∵AB∥FG,∴PQ∥AB,又∵AC∥BQ,∴四边形ABQC为平行四边形,∴AB=CQ=10,∵在Rt△ABC中,AC2+BC2=AB2,即5a2=100,∴a=2 或a=-2 (舍),∴AC=2 ,BC=4 ,∴CJ= = =4,∵JR=AF=AB=10,∴CR=CJ+JR=14.故选A.
二、填空题(每小题5分,共20分)6.(2019贵州毕节,17)如图,以△ABC的顶点B为圆心,BA长为半径画弧,交BC边于点D,连接AD.若∠B=40°, ∠C=36°,则∠DAC的大小为 度.
7.(2020广东,15)如图,在菱形ABCD中,∠A=30°,取大于 AB的长为半径,分别以点A,B为圆心作弧相交于两点,过此两点的直线交AD边于点E(作图痕迹如图所示),连接BE,BD.则∠EBD的度数为 .
8.(2019山东枣庄,16)用一条宽度相等的足够长的纸条打一个结(如图1所示),然后轻轻拉紧、压平就可 以得到如图2所示的正五边形ABCDE.图中,∠BAC= .
9.(2019江苏苏州,15)“七巧板”是我们祖先的一项卓越创造,可以拼出许多有趣的图形,被誉为“东方 魔板”.图①是由边长为10 cm的正方形薄板分为7块制作成的“七巧板”,图②是用该“七巧板”拼成 的一个“家”的图形.该“七巧板”中7块图形之一的正方形边长为 cm(结果保留根号).
三、解答题(共4小题,共55分)10.(10分)(2019湖北黄石,21)如图,在△ABC中,∠BAC=90°,E为边BC上的点,且AB=AE,D为线段BE的中点, 过点E作EF⊥AE,过点A作AF∥BC,且AF、EF相交于点F.(1)求证:∠C=∠BAD;(2)求证:AC=EF.
证明 (1)∵AB=AE,D为线段BE的中点,∴AD⊥BC.∴∠C+∠DAC=90°.∵∠BAC=90°,∴∠BAD+∠DAC=90°,∴∠C=∠BAD.(2)∵AF∥BC,∴∠FAE=∠AEB.∵AB=AE,∴∠B=∠AEB,∴∠B=∠FAE,AB=AE,且∠BAC=∠AEF=90°,∴△ABC≌△EAF(ASA),∴AC=EF.
11.(15分)(2019辽宁本溪,21)如图,在四边形ABCD中,AB∥CD,AD⊥CD,∠B=45°,延长CD到点E,使DE= DA,连接AE.(1)求证:AE=BC;(2)若AB=3,CD=1,求四边形ABCE的面积.
解析 (1)证明:∵AB∥CD,∠B=45°,∴∠C+∠B=180°,∴∠C=135°.∵DE=DA,AD⊥CD,∴∠E=45°.∵∠E+∠C=180°,∴AE∥BC.又AB∥CD,∴四边形ABCE是平行四边形,∴AE=BC.(2)∵四边形ABCE是平行四边形,∴AB=CE=3,∴AD=DE=AB-CD=2,∴四边形ABCE的面积=3×2=6.
12.(15分)(2019广西百色,22)如图,菱形ABCD中,作BE⊥AD、CF⊥AB,分别交AD、AB的延长线于点E、 F.(1)求证:AE=BF;(2)若点E恰好是AD的中点,AB=2,求BD的值.
解析 (1)证明:∵四边形ABCD是菱形,∴AB=BC,AD∥BC,∴∠A=∠CBF.∵BE⊥AD,CF⊥AB,∴∠AEB=∠BFC=90°,∴△AEB≌△BFC(AAS),∴AE=BF.(2)∵E是AD的中点,BE⊥AD,∴直线BE是线段AD的垂直平分线,∴BD=AB=2.
13.(15分)(2019内蒙古通辽,25)如图,点P是正方形ABCD内的一点,连接CP,将线段CP绕点C顺时旋转90°, 得到线段CQ,连接BP,DQ.(1)如图1,求证:△BCP≌△DCQ;(2)如图,延长BP交直线DQ于点E.①如图2,求证:BE⊥DQ;②如图3,若△BCP为等边三角形,判断△DEP的形状,并说明理由.
解析 (1)证明:∵线段CP绕点C顺时针旋转90°至CQ.∴∠PCQ=90°,CP=CQ.∵四边形ABCD为正方形,∴BC=CD,∠BCD=90°,∴∠BCP=∠DCQ,∴△BCP≌△DCQ.(2)①由(1)知△BCP≌△DCQ,∴∠CDQ=∠CBP.设BE与DC交于点M,∵∠BMC=∠EMD,∴∠DEM=∠BCM=90°,∴BE⊥DQ.②△DEP为等腰直角三角形.理由:∵线段CP绕点C顺时针旋转90°至CQ.
2021版《5年中考3年模拟》全国版中考数学:21版53中考全国数学教参目录: 这是一份2021版《5年中考3年模拟》全国版中考数学:21版53中考全国数学教参目录,共2页。
2021版《5年中考3年模拟》全国版中考数学:§7.2 概 率: 这是一份2021版《5年中考3年模拟》全国版中考数学:§7.2 概 率,共21页。
2021版《5年中考3年模拟》全国版中考数学:§7.1 统 计: 这是一份2021版《5年中考3年模拟》全国版中考数学:§7.1 统 计,共21页。












