

2021版《5年中考3年模拟》全国版中考数学:§5.1 圆的性质
展开考点一 圆的有关概念和垂径定理
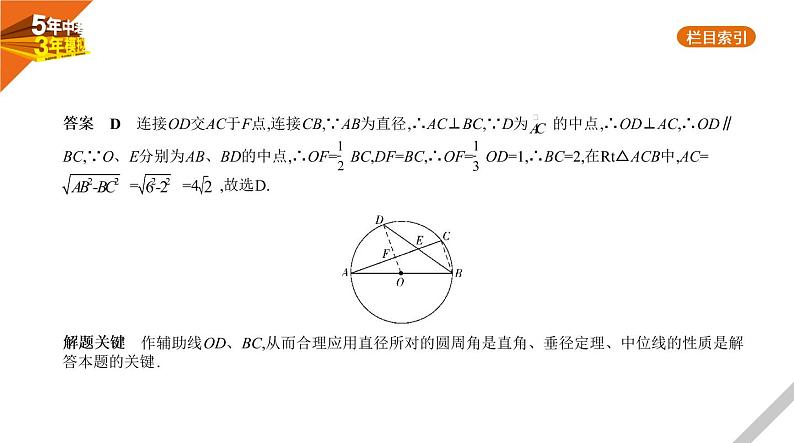
1.(2020湖北武汉,9,3分)如图,在半径为3的☉O中,AB是直径,AC是弦,D是 的中点,AC与BD交于点E.若E是BD的中点,则AC的长是 ( ) A. B.3 C.3 D.4
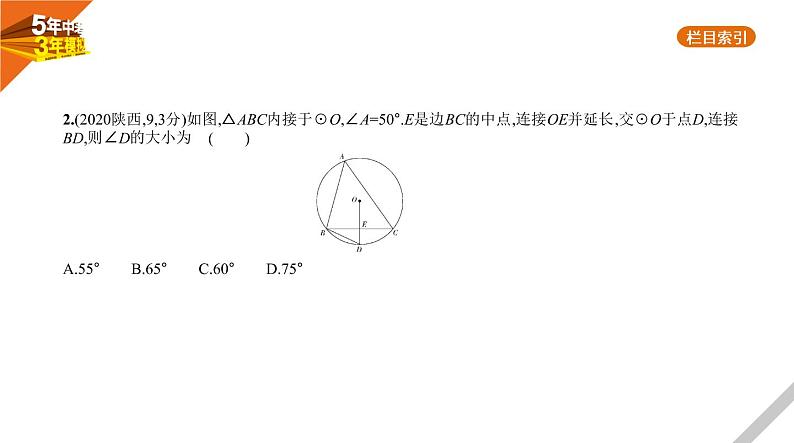
答案 D 连接OD交AC于F点,连接CB,∵AB为直径,∴AC⊥BC,∵D为 的中点,∴OD⊥AC,∴OD∥BC,∵O、E分别为AB、BD的中点,∴OF= BC,DF=BC,∴OF= OD=1,∴BC=2,在Rt△ACB中,AC= = =4 ,故选D.
解题关键 作辅助线OD、BC,从而合理应用直径所对的圆周角是直角、垂径定理、中位线的性质是解 答本题的关键.
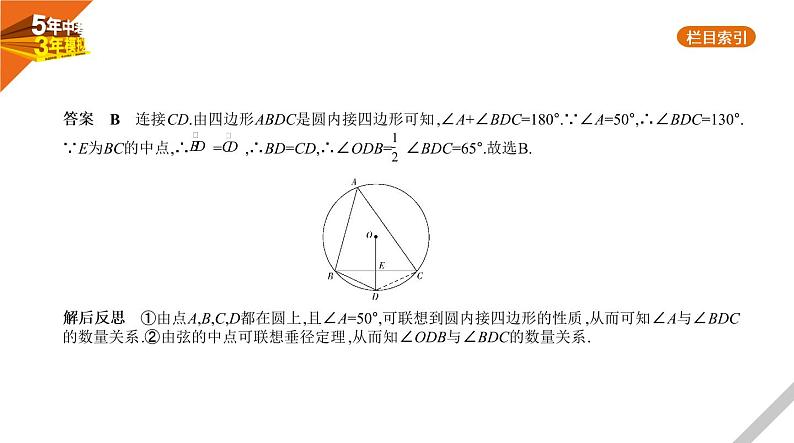
2.(2020陕西,9,3分)如图,△ABC内接于☉O,∠A=50°.E是边BC的中点,连接OE并延长,交☉O于点D,连接 BD,则∠D的大小为 ( ) A.55° B.65° C.60° D.75°
答案 B 连接CD.由四边形ABDC是圆内接四边形可知,∠A+∠BDC=180°.∵∠A=50°,∴∠BDC=130°. ∵E为BC的中点,∴ = ,∴BD=CD,∴∠ODB= ∠BDC=65°.故选B.
解后反思 ①由点A,B,C,D都在圆上,且∠A=50°,可联想到圆内接四边形的性质,从而可知∠A与∠BDC 的数量关系.②由弦的中点可联想垂径定理,从而知∠ODB与∠BDC的数量关系.
3.(2019湖北黄冈,7,3分)如图,一条公路的转弯处是一段圆弧( ),点O是这段弧所在圆的圆心,AB=40 m,点C是 的中点,点D是AB的中点,且CD=10 m.则这段弯路所在圆的半径为 ( ) A.25 m B.24 m C.30 m D.60 m
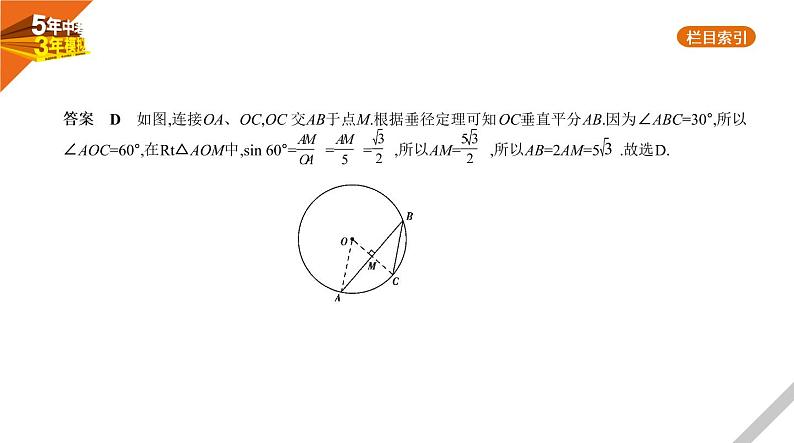
4.(2018山东威海,10,3分)如图,☉O的半径为5,AB为弦,点C为 的中点,若∠ABC=30°,则弦AB的长为 ( ) A. B.5 C. D.5
答案 D 如图,连接OA、OC,OC 交AB于点M.根据垂径定理可知OC垂直平分AB.因为∠ABC=30°,所以 ∠AOC=60°,在Rt△AOM中,sin 60°= = = ,所以AM= ,所以AB=2AM=5 .故选D.
5.(2017新疆,9,5分)如图,☉O的半径OD垂直于弦AB,垂足为点C.连接AO并延长交☉O于点E,连接BE,CE, 若AB=8,CD=2,则△BCE的面积为 ( ) A.12 B.15 C.16 D.18
答案 A ∵☉O的半径OD垂直于弦AB,AB=8,∴AC=BC= AB=4.设OA=r,则OC=OD-CD=r-2,在Rt△AOC中,由勾股定理得42+(r-2)2=r2,解得r=5,∴AE=10.∵AE为☉O的直径,∴AB⊥BE.在Rt△ABE中,BE= = =6,∴S△BCE= BC·BE= ×4×6=12.故选A.
考点二 圆心角、圆周角、弧、弦之间的关系
1.(2020海南,10,3分)如图,已知AB是☉O的直径,CD是弦,若∠BCD=36°,则∠ABD等于 ( ) A.54° B.56° C.64° D.66°
答案 A 根据圆周角定理的推论得∠BCD=∠A,∵∠BCD=36°,∴∠A=36°,根据直径所对的圆周角是 直角可得∠ADB=90°,∴∠ABD=90°-36°=54°,故选A.
2.(2020辽宁营口,7,3分)如图,AB为☉O的直径,点C,点D是☉O上的两点,连接CA,CD,AD,若∠CAB=40°,则 ∠ADC的度数是 ( ) A.110° B.130° C.140° D.160°
答案 B 连接CB,∵AB是☉O的直径,∴∠ACB=90°,∴∠ABC=90°-∠CAB=50°.∵四边形ADCB是圆内 接四边形,∴∠ADC=180°-∠ABC=130°.故选B.
3.(2019吉林,5,2分)如图,在☉O中, 所对的圆周角∠ACB=50°,若P为 上一点,∠AOP=55°,则∠POB的度数为 ( ) A.30° B.45° C.55° D.60°
答案 B 由题意可得∠AOB=2∠ACB=100°.∴∠POB=100°-55°=45°.故选B.
4.(2019陕西,9,3分)如图,AB是☉O的直径,EF、EB是☉O的弦,且EF=EB,EF与AB交于点C,连接OF.若∠ AOF=40°,则∠F的度数是 ( ) A.20° B.35° C.40° D.55°
答案 B 连接OE.∵EF=EB,∴∠EOF=∠EOB.∵∠AOF=40°,∴∠BOF=180°-∠AOF=140°,∴∠EOF=∠EOB= ×(360°-140°)=110°.∵OE=OF,∴∠F=∠OEF= (180°-∠EOF)=35°,故选B.
5.(2018湖北武汉,10,3分)如图,在☉O中,点C在优弧 上,将弧 折叠后刚好经过AB的中点D.若☉O的半径为 ,AB=4,则BC的长是 ( ) A.2 B.3 C. D.
答案 B 连接AO,并延长交☉O于点D',连接BD',则∠ABD'=90°.连接CD',DD',DD'交BC于点E,连接OD, OB,OC.∵D为AB的中点,∴OD⊥AB.∵AB=4,∴BD= AB=2.∵OB= ,∴OD= =1,∴BD'=2OD=2,即BD= BD',显然点D与点D'关于直线BC对称.∵∠ABD'=90°,∴∠ABC=∠CBD'=45°,根据圆周角定理得 ∠AOC=90°,∴∠D'OC=90°,∴CD'= OC= .∵∠CBD'=45°,BD'=2,∴BE=ED'= ,根据勾股定理得CE= =2 ,所以BC=BE+CE=3 ,故选B.
方法指导 在求解涉及圆的性质的问题时,通常运用垂径定理或圆周角定理得到相等的线段或角或垂 直关系,求解过程中常需作合适的辅助线构造直角三角形,利用勾股定理等知识进行求解.
6.(2020四川南充,16,4分)△ABC内接于☉O,AB为☉O的直径,将△ABC绕点C旋转到△EDC,点E在☉O上, 已知AE=2,tan D=3,则AB= .
解析 ∵AB为☉O的直径,∴∠AEB=∠ACB=90°,∴∠ECD=∠ACB=90°,∴tan D= =3.设CE=3x(x>0),CD=x,则DE= x,∴AB=DE= x.∵AC=CE,BC=CD,∠ACB=∠ECD,∴ = ,∠ACE=∠BCD,∴△ACE∽△BCD,∴ = =3,∴BD= ,∴BE=DE-BD= x- .
∵AE2+BE2=AB2,∴22+ =( x)2,∴x= ,∴AB= .
7.(2019内蒙古包头,24,10分)如图,在☉O中,B是☉O上一点,∠ABC=120°,弦AC=2 ,弦BM平分∠ABC交AC于点D,连接MA,MC. (1)求☉O半径的长;(2)求证:AB+BC=BM.
解析 (1)∵∠ABC=120°,BM平分∠ABC,∴∠MBA=∠MBC= ∠ABC=60°.易知∠ACM=∠ABM=60°,∠MAC=∠MBC=60°,∴△AMC是等边三角形.如图,连接OA,OC, ∴AO=CO,∠AOC=2∠AMC=120°,∴∠OAC=∠OCA=30°.作OH⊥AC于点H,
∴AH=CH= AC= .在Rt△AOH中,cs∠OAH= ,即 = ,∴AO=2.∴☉O的半径为2. (4分)(2)证明:在BM上截取BE=BC,连接CE.∵∠MBC=60°,BE=BC,∴△EBC为等边三角形,∴CE=CB=BE,∠BCE=60°,∴∠BCD+∠DCE=60°.∵∠ACM=60°,∴∠ECM+∠DCE=60°,∴∠ECM=∠BCD.∵△AMC为等边三角形,∴AC=MC,∴△ACB≌△MCE,∴AB=ME.∵ME+EB=BM,∴AB+BC=BM. (10分)
考点三 圆内接三角形、四边形
1.(2020吉林,6,2分)如图,四边形ABCD内接于☉O.若∠B=108°,则∠D的大小为 ( ) A.54° B.62° C.72° D.82°
答案 C 根据圆内接四边形的性质得∠B+∠D=180°,∵∠B=108°,∴∠D=180°-108°=72°,故选C.
2.(2019甘肃兰州,6,4分)如图,四边形ABCD内接于☉O,若∠A=40°,则∠C= ( ) A.110° B.120° C.135° D.140°
答案 D 由圆的内接四边形的性质可得∠A+∠C=180°,∴∠C=180°-40°=140°,故选D.
3.(2020贵州贵阳,14,4分)如图,△ABC是☉O的内接正三角形,点O是圆心,点D,E分别在边AC,AB上,若DA =EB,则∠DOE的度数是 度.
解析 连接OA,OB,∵△ABC是☉O的内接正三角形,∴∠AOB=2∠ACB=120°,∵AO=BO,∴∠OAB=∠OBA= (180°-∠AOB)=30°,∴∠DAO=∠CAB-∠OAB=30°,∵AD=BE,OA=OB,∴△OAD≌△OBE(SAS),∴∠DOA=∠EOB,∴∠DOE=∠DOA+∠AOE=∠EOB+∠AOE=∠AOB=120°.
4.(2018内蒙古呼和浩特,12,3分)同一个圆的内接正方形和正三角形的边心距的比为 .
1.(2018山东菏泽,6,3分)如图,在☉O中,OC⊥AB,∠ADC=32°,则∠OBA的度数是 ( ) A.64° B.58° C.32° D.26°
2.(2020宁夏,12,3分)我国古代数学经典著作《九章算术》中记载了一个“圆材埋壁”的问题:“今有圆 材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?”意思是:今有一圆柱形木材,埋在墙壁 中,不知其大小.用锯去锯这木材,锯口深ED=1寸,锯道长AB=1尺(1尺=10寸).这根圆柱形木材的直径是 寸.
解析 由垂径定理可知OE垂直平分AB,∴AD=5寸,设半径OA=x寸,则OD=(x-1)寸.在Rt△AOD中,AD2+ OD2=OA2,∴52+(x-1)2=x2,解得x=13,∴直径为26寸.
3.(2019安徽,19,10分)筒车是我国古代发明的一种水利灌溉工具.如图1,明朝科学家徐光启在《农政全 书》中用图画描绘了筒车的工作原理.如图2,筒车盛水桶的运行轨道是以轴心O为圆心的圆.已知圆心在 水面上方,且圆被水面截得的弦AB的长为6米,∠OAB=41.3°.若点C为运行轨道的最高点(C,O的连线垂直 于AB),求点C到弦AB所在直线的距离.(参考数据:sin 41.3°≈0.66,cs 41.3°≈0.75,tan 41.3°≈0.88) 图1 图2
解析 连接CO并延长,交AB于点D,则CD⊥AB,所以D为AB的中点,所求运行轨道的最高点C到弦AB所在 直线的距离即为线段CD的长. 在Rt△AOD中,∵AD= AB=3,∠OAD=41.3°,∴OD=AD·tan 41.3°≈3×0.88=2.64,OA= ≈ =4,∴CD=CO+OD=AO+OD=4+2.64=6.64.答:运行轨道的最高点C到弦AB所在直线的距离约为6.64米. (10分)
思路分析 本题考查垂径定理和三角函数的应用,通过垂径定理求得AD的长,再通过解三角形,求得AO 和OD的长,从而求出点C到弦AB所在直线的距离.
1.(2018江苏淮安,8,3分)如图,点A、B、C、D在☉O上,∠AOC=140°,点B是 的中点,则∠D的度数是 ( ) A.70° B.55° C.35.5° D.35°
答案 D 如图,连接OB.∵点B是 的中点,∴ = ,∴∠AOB= ∠AOC= ×140°=70°,∴∠D= ∠AOB= ×70°=35°.
方法总结 在圆中,见到弧的中点时,就要想到等弧、相等的圆心角、圆周角以及相等的弦.
2.(2017陕西,9,3分)如图,△ABC是☉O的内接三角形,∠C=30°,☉O的半径为5.若点P是☉O上的一点,在△ ABP中,PB=AB,则PA的长为 ( ) A.5 B. C.5 D.5
答案 D 连接OB、OA、OP. ∵∠C=30°,∴∠AOB=60°.∵OA=OB,∴△OAB是等边三角形,∴AB=5.∵PB=AB=OA=OP,∴四边形OABP是菱形,∴OB⊥AP,∴AP=2AB·cs 30°=2×5×cs 30°=2×5× =5 .故选D.
3.(2018甘肃武威,9,3分)如图,☉A过点O(0,0),C( ,0),D(0,1),点B是x轴下方☉A上的一点,连接BO,BD,则∠OBD的度数是 ( ) A.15° B.30° C.45° D.60°
4.(2020四川成都,13,4分)如图,A,B,C是☉O上的三个点,∠AOB=50°,∠B=55°,则∠A的度数为 .
5.(2018吉林,13,3分)如图,A,B,C,D是☉O上的四个点, = .若∠AOB=58°,则∠BDC= 度.
6.(2019浙江温州,14,5分)如图,☉O分别切∠BAC的两边AB,AC于点E,F,点P在优弧( )上.若∠BAC=66°,则∠EPF等于 度.
7.(2019天津,18,3分)如图,在每个小正方形的边长均为1的网格中,△ABC的顶点A在格点上,B是小正方形 边的中点,∠ABC=50°,∠BAC=30°,经过点A,B的圆的圆心在边AC上.(1)线段AB的长等于 ;(2)请用 的直尺,在如图所示的网格中,画出一个点P,使其满足∠PAC=∠PBC=∠PCB,并简要说明点P的位置是如何找到的(不要求证明) .
答案 (1) (2)如图,取圆与网格线的交点E、F,连接EF,与AC相交,得圆心O;AB与网格线相交于点D,连接DO并延长, 交☉O于点Q,连接QC并延长,与点B,O的连线BO相交于点P,连接AP,则点P满足∠PAC=∠PBC=∠PCB
解析 (1)根据勾股定理得AB= = .(2)取圆与网格线的交点E、F,连接EF与AC相交,根据90度的圆周角所对的弦是直径,可得EF与AC的交 点为圆心O;AB与网格线相交于点D,连接DO并延长交☉O于点Q,连接QC并延长,与点B,O的连线BO相交 于点P,连接AP.由图形可知点D为AB的中点,OD⊥AB,∵OA=OB,∠BAC=30°,∴∠BAC=∠ABO=30°,∠AOD=∠BOD=60°,∴∠BOC=60°,∵∠ABC=50°,∴∠CBP=20°,∵∠AOD=∠COQ=60°,∴∠BOC=∠COQ.∵OB=OQ,OC=OC,∴△COQ≌△COB,∴∠Q=∠CBO=20°,∵∠AOP=∠POQ=120°,且OA=OQ,OP=OP,
∴△POQ≌△POA,∴∠Q=∠CAP=20°,∵∠ABC=50°,∠BAC=30°,∴∠ACB=100°,∵∠ACP=∠Q+∠COQ=20°+60°=80°,∴∠PCB=∠ACB-∠ACP=100°-80°=20°,∴∠PAC=∠PBC=∠PCB=20°,点P符合条件.
难点突破 点P位置的确定需要学生清楚∠BAC=30°,经过点A、B的圆的圆心在边AC上,进而确定圆心 位置,利用圆的对称性把∠PAC转化到∠Q,最后只要求∠PCB=20°,便可把所求问题进行有效转化,显然 射线QC与线段OB的交点即为所求的点P.
8.(2019福建,24,12分)如图,四边形ABCD内接于☉O,AB=AC,AC⊥BD,垂足为E,点F在BD的延长线上,且 DF=DC,连接AF,CF.(1)求证:∠BAC=2∠CAD;(2)若AF=10,BC=4 ,求tan∠BAD的值.
解析 (1)证明:∵AC⊥BD,∴∠AED=90°,在Rt△AED中,∠ADE=90°-∠CAD.∵AB=AC,∴ = ,∴∠ACB=∠ABC=∠ADE=90°-∠CAD.在△ABC中,∠BAC+∠ABC+∠ACB=180°,∴∠BAC=180°-(∠ABC+∠ACB)=180°-2(90°-∠CAD),即∠BAC=2∠CAD.(2)∵DF=DC,∴∠FCD=∠CFD.∵∠BDC=∠FCD+∠CFD,∴∠BDC=2∠CFD.∵∠BDC=∠BAC,且由(1)知∠BAC=2∠CAD,∴∠CFD=∠CAD,∵∠CAD=∠CBD,∴∠CFD=∠CBD,∴CF=CB.∵AC⊥BF,∴BE=EF,故CA垂直平分BF,∴AC=AB=AF=10.设AE=x,则CE=10-x.
在Rt△ABE和Rt△BCE中,AB2-AE2=BE2=BC2-CE2,又∵BC=4 ,∴102-x2=(4 )2-(10-x)2,解得x=6.∴AE=6,CE=4,∴BE= =8.∵∠DAE=∠CBE,∠ADE=∠BCE,∴△ADE∽△BCE,∴ = = ,∴DE=3,AD=3 .过点D作DH⊥AB,垂足为H.
∵S△ABD= AB·DH= BD·AE,BD=BE+DE=11,∴10DH=11×6,故DH= .在Rt△ADH中,AH= = ,∴tan∠BAD= = .说明:本参考答案仅给出一种解法供参考.
1.(2019四川成都,9,3分)如图,正五边形ABCDE内接于☉O,P为 上的一点(点P不与点D重合),则∠CPD的度数为 ( ) A.30° B.36° C.60° D.72°
2.(2018四川自贡,9,4分)如图,若△ABC内接于半径为R的☉O,且∠A=60°,连接OB、OC,则边BC的长为 ( ) A.R B. R C. R D. R
答案 D 作OH⊥BC于H.由圆周角定理得∠BOC=2∠A=120°.因为OH⊥BC,OB=OC,所以BH=HC,∠BOH=∠HOC=60°.在Rt△BOH中,BH=OB·sin 60°= R,∴BC=2BH= R.
3.(2019山东潍坊,11,3分)如图,四边形ABCD内接于☉O,AB为直径,AD=CD,过点D作DE⊥AB于点E,连接 AC交DE于点F.若sin∠CAB= ,DF=5,则BC的长为 ( ) A.8 B.10 C.12 D.16
答案 C 连接BD,如图, ∵AB为直径,∴∠ADB=∠ACB=90°,∵AD=CD,∴∠DAC=∠DCA,又∠DCA=∠ABD,∴∠DAC=∠ABD,∵DE⊥AB,∴∠ABD+∠BDE=90°,又∠ADE+∠BDE=90°,∴∠ABD=∠ADE,∴∠ADE=∠DAC,
∴FD=FA=5.在Rt△AEF中,∵sin∠FAE= = ,∴EF=3,∴AE= = =4,DE=DF+EF=5+3=8,∵∠ADE=∠DBE,∠AED=∠BED,∴△ADE∽△DBE,∴DE∶BE=AE∶DE,即8∶BE=4∶8,∴BE=16,∴AB=AE+BE=4+16=20,在Rt△ABC中,∵sin∠CAB= = ,∴BC=20× =12.故选C.
思路分析 连接BD,由圆周角定理及AD=CD可得∠ADE=∠DAC,进而得到FD=FA=5,在Rt△AEF中,根 据正弦的定义计算出EF=3,则AE=4,DE=8,接着证明△ADE∽△DBE,利用对应边成比例得到BE=16,则 AB=20,然后在Rt△ABC中,利用正弦的定义计算出BC的长.
4.(2018四川内江,24,6分)已知△ABC的三边a、b、c满足a+b2+|c-6|+28=4 +10b,则△ABC的外接圆半径= .
解析 ∵a+b2+|c-6|+28=4 +10b,∴(a-1-4 +4)+(b2-10b+25)+|c-6|=0,∴( -2)2+(b-5)2+|c-6|=0,∴ -2=0,b-5=0,c-6=0,解得a=5,b=5,c=6,∴AC=BC=5,AB=6,作CD⊥AB于点D,连接OA,则点O在CD上,AD=3,CD=4,设△ABC的外接圆的半径为r,则OC=r,OD=4-r,OA=r,∴32+(4-r)2=r2,解得r= ,即△ABC的外接圆半径为 .
设计意图 本题巧妙地把三角形外接圆与非负数性质结合起来,先用非负数的性质求出三角形的三边 长,再用勾股定理把外接圆半径与边长联系起来,难度不大,但需要一定的思维能力及多角度思考问题的 能力.
5.(2019陕西,17,5分)如图,在△ABC中,AB=AC,AD是BC边上的高.请用尺规作图法,求作△ABC的外接圆. (保留作图痕迹,不写作法)
6.(2020内蒙古呼和浩特,23,10分)某同学在学习了正多边形和圆之后,对正五边形的边及相关线段进行 研究,发现多处出现著名的黄金分割比 ≈0.618.如图,圆内接正五边形ABCDE,圆心为O,OA与BE交于点H,AC,AD与BE分别交于点M、N.根据圆与正五边形的对称性,只对部分图形进行研究.(其他可同理 得出)(1)求证:△ABM是等腰三角形且底角等于36°,并直接说出△BAN的形状;(2)求证: = ,且其比值k= ;(3)由对称性知AO⊥BE,由(1)(2)可知 也是一个黄金分割数,据此求sin 18°的值.
解析 (1)连接圆心O与正五边形除A外的各顶点,在正五边形中,∠AOE=360°÷5=72°,∴∠ABE= ∠AOE=36°,同理∠BAC= ×72°=36°,∴AM=BM,∴△ABM是等腰三角形且底角等于36°.∵∠BOD=∠BOC+∠COD=72°+72°=144°,∴∠BAD= ∠BOD=72°,∴∠BNA=180°-∠BAD-∠ABE=72°,∴AB=NB,即△ABN为等腰三角形.
(2)证明:∵∠ABM=∠ABE,∠AEB= ∠AOB=36°=∠BAM,∴△BAM∽△BEA,∴ = ,而AB=BN,∴ = ,设BM=y,AB=x,则AM=AN=y,AE=BN=x,∵∠AMN=∠MAB+∠MBA=72°=∠BAN,∠ANM=∠ANB,∴△AMN∽△BAN,∴ = ,即 = ,则y2=x2-xy,
两边同除以x2,得 =1- ,设 =t,则t2+t-1=0,解得t= 或 (舍),∴ = = = .(3)∵∠MAN=36°,根据对称性可知:∠MAH=∠NAH= ∠MAN=18°,而AO⊥BE, = ,∴sin 18°=sin∠MAH= = = = .
7.(2020陕西,25,12分)问题提出(1)如图1,在Rt△ABC中,∠ACB=90°,AC>BC,∠ACB的平分线交AB于点D.过点D分别作DE⊥AC,DF⊥ BC,垂足分别为E,F,则图1中与线段CE相等的线段是 ;问题探究(2)如图2,AB是半圆O的直径,AB=8.P是 上一点,且 =2 ,连接AP,BP.∠APB的平分线交AB于点C,过点C分别作CE⊥AP,CF⊥BP,垂足分别为E,F,求线段CF的长;问题解决(3)如图3,是某公园内“少儿活动中心”的设计示意图.已知☉O的直径AB=70 m,点C在☉O上,且CA=CB. P为AB上一点,连接CP并延长,交☉O于点D,连接AD,BD.过点P分别作PE⊥AD,PF⊥BD,垂足分别为E,F. 按设计要求,四边形PEDF内部为室内活动区,阴影部分是户外活动区,圆内其余部分为绿化区.设AP的长 为x(m),阴影部分的面积为y(m2).①求y与x之间的函数关系式;②按照“少儿活动中心”的设计要求,发现当AP的长度为30 m时,整体布局比较合理.试求当AP=30 m 时,室内活动区(四边形PEDF)的面积.
图1 图2 图3
解析 (1)CF,FD,DE. (3分)详解:∵∠ACB=90°,DE⊥AC,DF⊥BC,∴四边形DFCE是矩形.又∵CD是∠ACB的平分线,∴DE=DF,∴四边形DFCE是正方形.∴CE=CF=DF=DE.(2)如图,连接OP. ∵AB是直径, =2 ,∴∠AOP=60°.∴∠B=30°.
由题意知,矩形PECF为正方形. (5分)在Rt△APB中,PB=AB·cs 30°=4 .在Rt△CBF中,BF= = CF.∵PF=CF,∴CF+ CF=4 .∴CF=6-2 . (7分)(3)如图.①∵AB为直径,∴∠ACB=∠ADB=90°.∵AC=BC,∴∠ADC=∠BDC.∴PE=PF.∴四边形PEDF为正方形.∴∠APE+∠BPF=90°,∠PEA=∠PFB=90°.∴将△APE绕点P逆时针旋转90°,得到△A'PF,PA'=PA,则A'、F、B三点共线,△PA'B为直角三角形,∠A'PB=90°.∴S△PAE+S△PBF=S△PA'B= PA'·PB= x(70-x). (9分)
在Rt△ABC中,AC=BC=35 ,∴S△ABC= AC2=1 225.∴y=S△PA'B+S△ABC= x(70-x)+1 225=- x2+35x+1 225.(10分) ②当x=30时,PA'=30,PB=40.在Rt△PA'B中,A'B= =50.∵S△PA'B= A'B·PF= PB·PA',
∴ ×50×PF= ×30×40.∴PF=24.∴S四边形PEDF=PF2=242=576(m2).∴当AP=30 m时,室内活动区(四边形PEDF)的面积为576 m2. (12分)
A组 2018—2020年模拟·基础题组时间:45分钟 分值:50分一、选择题(每小题3分,共15分)
1.(2020广西崇左江州一模,6)如图,圆O是△ABC的外接圆,∠A=68°,则∠OBC的大小是 ( ) A.22° B.26° C.32° D.68°
2.(2020辽宁鞍山铁东一模,6)如图,在☉O中,弦AB垂直平分半径OC,OC=2,则弦AB的长为 ( ) A.2 B. C.2 D.
3.(2020北京朝阳一模,6)如图,☉O的直径AB垂直于弦CD,垂足为E,CD=4,tan C= ,则AB的长为 ( ) A.2.5 B.4 C.5 D.10
4.(2019新疆乌鲁木齐高新区一模,8)如图,☉O中,半径OC⊥弦AB于点D,点E在☉O上,∠E=22.5°,AB=4,则 半径OB等于 ( ) A. B.2 C.2 D.3
5.(2019云南曲靖一模,7)如图,四边形ABCD是☉O的内接四边形,若∠BOD=144°,则∠C的度数是 ( ) A.14° B.72° C.36° D.108°
二、填空题(每小题3分,共15分)6.(2020北京密云一模,13)如图,AB为☉O的直径,点C为☉O上一点,点D为 的中点,且OD与AC相交于点E,若☉O的半径为4,∠CAB=30°,则弦AC的长度为 .
7.(2020福建泉州模拟,13)如图,☉O是△ABC的外接圆,∠A=45°,则cs∠OCB的值是 .
8.(2019四川成都武侯模拟,13)如图,M是△ABC中BC边上的一点,AM的延长线交△ABC的外接圆于D,已 知:AD=12 cm,BD=CD=6 cm,则DM的长为 cm.
9.(2019湖北襄阳襄州模拟,15)如图,在☉O的内接五边形ABCDE中,∠B+∠E=210°,则∠CAD= °.
10.(2019黑龙江哈尔滨香坊一模,18)如图,AB是☉O的直径,∠ABT=50°,BT交☉O于点C,E是AB上一点,延 长CE交☉O于点D,连接BD,则∠CDB的度数是 °.
三、解答题(共20分)11.(2020广西崇左江州一模,23)如图,☉O是△ABC的外接圆,AB为直径,OD∥BC交☉O于点D,交AC于点 E,连接AD,BD,CD.(1)求证:AD=CD;(2)若AB=10,cs∠ABC= ,求tan∠DBC的值.
解析 (1)证明:∵AB为☉O的直径,∴∠ACB=90°.∵OD∥BC,∴∠AEO=∠ACB=90°,∴OD⊥AC,∴ = ,∴AD=CD.(2)∵AB=10,∴OA=OD= AB=5.∵OD∥BC,∴∠AOE=∠ABC.在Rt△AEO中,OE=OA·cs∠AOE=OA·cs∠ABC=5× =3,∴DE=OD-OE=5-3=2,AE= = =4.在Rt△AED中,tan∠DAE= = = ,∵∠DBC=∠DAE,∴tan∠DBC= .
12.(2019上海金山一模,22)如图,已知AB是半圆O的直径,C为半圆上一点,D是 的中点,CH⊥AB于H,垂足为H,连接OD交弦BC于E,交CH于F,连接EH.(1)求证:△BHE∽△BCO;(2)若OC=4,BH=1,求EH的长.
解析 (1)证明:∵OD为半圆O的半径,D是 的中点,∴OD⊥BC,BE=CE= BC.∵CH⊥AB,∴∠CHB=90°,∴HE= BC=BE,∴∠B=∠EHB.∵OB=OC,∴∠B=∠OCB,∴∠EHB=∠OCB,又∵∠B=∠B,∴△BHE∽△BCO.(2)∵△BHE∽△BCO,∴ = .∵OC=OB=4,BH=1,∴ = ,解得BE= (舍负),∴EH=BE= .
13.(2019湖北武汉东西湖区模拟,21)如图,在Rt△ABC中,∠ACB=90°,以BC为直径的☉O交AB于点D,E为 的中点,CE交AB于点H,且AH=AC,AF平分∠CAH交BC于F.(1)求证:BE∥AF;(2)若AC=6,BC=8,求EH的长.
解析 (1)证明:∵AH=AC,AF平分∠CAH,∴∠HAF=∠CAF,AF⊥EC,∴∠HAF+∠ACH=90°.∵∠ACB=90°,即∠BCE+∠ACH=90°,∴∠HAF=∠BCE.∵E为 的中点,∴ = ,∴∠EBD=∠BCE,∴∠HAF=∠EBD,∴BE∥AF.(2)连接OH、CD.∵BC为☉O的直径,∴∠BDC=90°.∵∠ACB=90°,AC=6,BC=8,∴AB= = =10.∵AH=AC=6,∴BH=AB-AH=10-6=4.∵∠EBH=∠ECB,∠BEH=∠CEB,∴△EBH∽△ECB,∴ = = ,∴EB=2EH.在Rt△EBH中,由勾股定理得BE2+EH2=BH2,即(2EH)2+EH2=42,∴EH= (舍负).
B组 2018—2020年模拟·提升题组时间:30分钟 分值:45分一、选择题(每小题3分,共15分)
1.(2020福建福清模拟,9)已知△ABC内接于☉O,连接AO并延长交BC于点D,若∠B=62°,∠C=50°,则∠ ADB的度数是 ( ) A.68° B.72° C.78° D.82°
答案 C 延长AD交☉O于E,连接CE, 则∠E=∠B=62°,∠ACE=90°,∴∠CAE=90°-62°=28°,∴∠ADB=∠CAE+∠ACB=78°,故选C.
2.(2020陕西西安西北工大附中二模,9)如图,四边形ABCD内接于半径为6的☉O中,连接AC,若AB=CD,∠ ACB=45°,∠ACD= ∠BAC,则BC的长度为 ( ) A.6 B.6 C.9 D.9
答案 A 连接OA、OB,作BH⊥AC于H,如图, ∵AB=CD,∴ = ,∴∠CAD=∠ACB=45°.∵∠BCD+∠BAD=180°,即∠ACD+∠ACB+∠CAD+∠BAC=180°,又∠ACD= ∠BAC,∴ ∠BAC+45°+45°+∠BAC=180°,解得∠BAC=60°.∵∠AOB=2∠ACB=90°,OA=OB,∴△OAB为等腰直角三角形,∴AB= OA=6 .
在Rt△ABH中,∵∠BAH=60°,∴BH=AB·sin∠BAH=6 × =3 .在Rt△BCH中,∵∠BCH=45°,∴BC= BH= ×3 =6 .故选A.
3.(2020海南琼海一模,12)如图,四边形ABCD内接于☉O,AB=9,AD=15,∠BCD=120°,AC平分∠BAD,则弦 AC的长是 ( ) A.7 B.8 C.12 D.13
答案 B 过C作CE⊥AD于E,CF⊥AB交AB的延长线于F,则∠BFC=∠DEC=90°.∵AC平分∠BAD,CF⊥AF,CE⊥AD,∴CF=CE.由勾股定理得AF2=AC2-CF2,AE2=AC2-CE2,∴AF=AE.∵A、B、C、D四点共圆,∴∠FBC=∠D,∠BAD+∠BCD=180°,又∵∠BCD=120°,∴∠BAD=60°.∵AC平分∠BAD,∴∠BAC=∠DAC=30°.在△FBC和△EDC中, ∴△FBC≌△EDC(AAS),∴BF=DE.∵AB=9,AD=15,∴AF+AE=AB+BF+AD-DE=9+BF+15-DE=9+15=24,
∴AF=AE=12. ∵∠BAC=30°,∠AFC=90°,∴AC=2CF,∴CF2+122=(2CF)2,解得CF=4 (舍负),∴AC=2CF=8 ,故选B.
4.(2019湖北武汉硚口一模,10)如图,正方形ABCD和正△AEF都内接于☉O,EF与BC、CD分别相交于 点G、H.若AE=3,则EG的长为 ( ) A. B. C. D.
答案 B 如图,连接AC、BD、OF,则AC与BD交于点O,设AC交EF于点I,☉O的半径是r, 则OF=OA=r,易知AO是∠EAF的平分线,∴∠OAF=60°÷2=30°,AC⊥EF,EI= EF= .∵OA=OF,∴∠OFA=∠OAF=30°,∴∠COF=30°+30°=60°,∴FI=r·sin 60°= r,∴EF= r×2= r=AE=3,
∴r= ,∴OI= ,∴CI=OC-OI= .∵EF⊥AC,∠BCA=45°,∴∠IGC=∠BCI=45°.∴CI=GI= ,∴EG=EI-GI= - = ,故选B.
5.(2018四川内江资中一模,12)在半径等于5 cm的圆内有长为5 cm的弦,则此弦所对的圆周角为 ( )A.120° B.30°或120°C.60° D.60°或120°
∴OD平分∠AOB,即∠AOD=∠BOD= ∠AOB,∴在直角三角形AOD中,sin∠AOD= = ,∴∠AOD=60°,∴∠AOB=120°,又圆心角∠AOB(小于180°的∠AOB)与圆周角∠AEB所对的弧都为劣弧AB,∴∠AEB= ∠AOB=60°.∵四边形AEBF为圆O的内接四边形,∴∠AFB+∠AEB=180°,∴∠AFB=180°-∠AEB=120°.则弦AB所对的圆周角为60°或120°.故选D.
二、填空题(每小题3分,共9分)6.(2020上海嘉定二模,16)如图,点A、B、C在☉O上,其中点C是劣弧AB的中点.请添加一个条件,使得四 边形AOBC是菱形,所添加的这个条件可以是 (使用数学符号语言表达).
答案 AC=AO(或AC=OB或∠AOB=120°或OA∥CB等)
7.(2019云南昆明模拟,4)如图,AB是☉O的直径,C,D两点在☉O上,若∠BCD=40°,则∠ABD的度数为 .
解析 ∵AB是☉O的直径,∴∠ACB=90°,∴∠ACD=90°-∠BCD=50°,∴∠ABD=∠ACD=50°.
8.(2019湖北仙桃模拟,15)如图,已知AB是☉O的直径,BC为弦,∠ABC=30度.过圆心O作OD⊥BC交弧BC 于点D,连接DC,则∠DCB= 度.
三、解答题(共21分)9.(2020四川成都龙泉驿三诊,20)如图,在△ABC中,AB=AC,以AB为直径的☉O分别交BC,AC于点D,E,连 接EB,OD,ED,设EB交OD于点F.(1)求证:OD⊥BE;(2)若DE= ,AB=10,求AE的长;(3)若△CDE的面积是△OBF的面积的 ,求 的值.
解析 (1)证明:连接AD,∵AB是☉O的直径,∴∠ADB=90°.∵AB=AC,∴∠BAD=∠CAD,∴ = ,∴OD⊥BE.(2)∵AB是☉O的直径,∴∠AEB=90°,∴∠BEC=90°.由(1)可知BD=CD=DE,∴BC=2DE=2 .∵四边形ABDE内接于☉O,∴∠BAC+∠BDE=180°.又∵∠CDE+∠BDE=180°,∴∠CDE=∠BAC.又∵∠C=∠C,∴△CDE∽△CAB,∴ = ,即 = ,∴CE=2,∴AE=AC-CE=AB-CE=8.(3)∵ = ,∴设S△CDE=5k,S△OBF=6k,k>0.
∵BD=CD,∴S△CDE=S△BDE=5k.∵BD=CD,AO=BO,∴OD∥AC,∴△OBF∽△ABE,∴ = = ,∴S△ABE=4S△OBF=24k,∴S△CAB=S△CDE+S△BDE+S△ABE=34k.由(2)知△CDE∽△CAB,∴ = = ,∴ = = ,∵BC=2CD,∴ = .
10.(2019黑龙江哈尔滨香坊一模,26)△ABC内接于☉O,AC为☉O的直径,∠A=60°,点D在AC上,连接BD, 作等边三角形BDE,连接OE.(1)如图1,求证:OE=AD;(2)如图2,连接CE,求证:∠OCE=∠ABD;(3)如图3,在(2)的条件下,延长EO交☉O于点G,在OG上取点F,使OF=2OE,延长BD到点M,使BD=DM,连接 MF,若tan∠BMF= ,OD=3,求线段CE的长.
解析 (1)证明:如图1所示,连接OB, 图1∵∠A=60°,OA=OB,∴△AOB为等边三角形,∴OA=OB=AB,∠A=∠ABO=∠AOB=60°.∵△DBE为等边三角形,∴DB=DE=BE,∠DBE=∠BDE=∠DEB=60°,∴∠ABD+∠DBO=∠DBO+∠OBE=60°,∴∠ABD=∠OBE,∴△ADB≌△OEB(SAS),∴OE=AD.(2)证明:如图2所示,连接OB.
由(1)可知△ADB≌△OEB,∴∠BOE=∠A=60°,又∵∠BOA=60°,∴∠EOC=60°,∴∠BOE=∠EOC.又∵OE=OE,OB=OC,∴△BOE≌△COE(SAS),∴∠OCE=∠OBE,∴∠OCE=∠ABD.(3)如图3所示,过点M作AB的平行线交AC于点Q,过点D作DN⊥EG于点N,连接MG.
∵MQ∥AB,∴∠QMD=∠ABD.∵∠ADB=∠QDM,BD=DM,∠ABD=∠QMD,∴△ADB≌△QDM(ASA),∴AB=MQ,AD=DQ.∵∠A=60°,∠ABC=90°,∴∠ACB=30°,∴AB= AC=AO=CO=OG,∴MQ=OG,易知AB∥GO,∴MQ∥GO,∴四边形MQOG为平行四边形.∴MG=OQ.设AD=x,则OE=x,OF=2x,∵OD=3,∴OA=OG=3+x,GF=3-x.∵DQ=AD=x,∴OQ=MG=3-x,∴MG=GF.∵∠DOG=60°,OQ∥MG,∴∠MGF=120°,∴∠GMF=∠GFM=30°.易知∠ABD=∠ODE,∠ODN=30°,∠QMF=∠MFG=30°,∴∠DMF=∠EDN.
中考数学模拟汇编一39圆的有关性质: 这是一份中考数学模拟汇编一39圆的有关性质,共25页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
中考数学模拟汇编二39圆的有关性质: 这是一份中考数学模拟汇编二39圆的有关性质,共13页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2021年全国中考数学真题分类汇编--圆 与圆的有关性质(无答案): 这是一份2021年全国中考数学真题分类汇编--圆 与圆的有关性质(无答案),共19页。












