
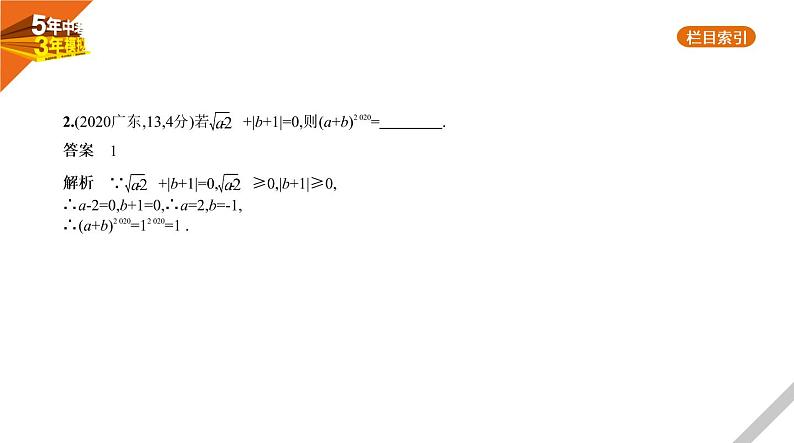




2021版《5年中考3年模拟》全国版中考数学:§1.2 整 式
展开1.(2018重庆A卷,8,4分)按如图所示的运算程序,能使输出的结果为12的是 ( ) A.x=3,y=3 B.x=-4,y=-2C.x=2,y=4 D.x=4,y=2
答案 C 由运算程序可知,需先判断y的符号,再进行代数式的选择.A选项中,y≥0,故将x、y的值代入x2 +2y,输出的结果为15;B选项中,y<0,故将x、y的值代入x2-2y,输出的结果为20;C选项中,y≥0,故将x、y的 值代入x2+2y,输出的结果为12;D选项中,y≥0,故将x、y的值代入x2+2y,输出的结果为20.故选C.
2.(2020广东,13,4分)若 +|b+1|=0,则(a+b)2 020= .
3.(2020四川成都,21,4分)已知a=7-3b,则代数式a2+6ab+9b2的值为 .
解析 ∵a=7-3b,∴a2+6ab+9b2=(7-3b)2+6·(7-3b)·b+9b2=49-42b+9b2+42b-18b2+9b2=49-42b+42b+9b2+9b2-18b2=49.
一题多解 ∵a2+6ab+9b2=(a+3b)2,a=7-3b,∴原式=(7-3b+3b)2=72=49.
4.(2018四川成都,21,4分)已知x+y=0.2,x+3y=1,则代数式x2+4xy+4y2的值为 .
解析 ∵x+y=0.2①,x+3y=1②,∴①+②得2x+4y=1.2,即x+2y=0.6.又∵x2+4xy+4y2=(x+2y)2,∴原式=0.62=0.3 6.
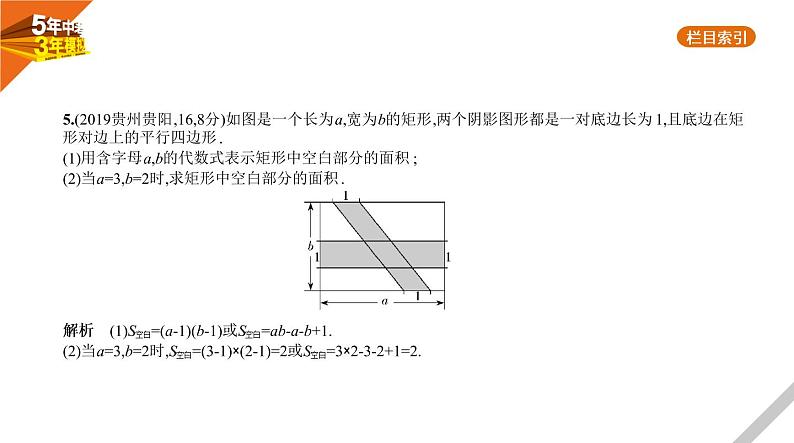
5.(2019贵州贵阳,16,8分)如图是一个长为a,宽为b的矩形,两个阴影图形都是一对底边长为1,且底边在矩 形对边上的平行四边形.(1)用含字母a,b的代数式表示矩形中空白部分的面积;(2)当a=3,b=2时,求矩形中空白部分的面积.
解析 (1)S空白=(a-1)(b-1)或S空白=ab-a-b+1.(2)当a=3,b=2时,S空白=(3-1)×(2-1)=2或S空白=3×2-3-2+1=2.
考点二 整式及其运算法则
1.(2020吉林,4,2分)下列运算正确的是 ( )A.a2·a3=a6 B.(a2)3=a5C.(2a)2=2a2 D.a3÷a2=a
答案 D a2·a3=a5,选项A错误;(a2)3=a6,选项B错误;(2a)2=4a2,选项C错误;a3÷a2=a,选项D正确.故选D.
解后反思 有关整式的计算问题,首先明确所考查的运算类型,再根据各自的运算法则计算即可.在运算 的过程中,一定要注意指数、系数和符号的处理,同时还应熟记乘法公式,灵活运用.
2.(2020四川成都,5,3分)下列计算正确的是 ( )A.3a+2b=5ab B.a3·a2=a6C.(-a3b)2=a6b2 D.a2b3÷a=b3
答案 C 3a和2b不是同类项,不能合并,故A错;a3·a2=a5,故B错;(-a3b)2=a6b2,故C对;a2b3÷a=ab3,故D错.故选 C.
3.(2020陕西,5,3分)计算: = ( )A.-2x6y3 B. x6y3C.- x6y3 D.- x5y4
方法指导 an·am=an+m,(anbm)k=ankbmk.
4.(2019新疆,4,5分)下列计算正确的是 ( )A.a2·a3=a6 B.(-2ab)2=4a2b2C.x2+3x2=4x4 D.-6a6÷(2a2)=-3a3
答案 B 因为a2·a3=a5,x2+3x2=4x2,-6a6÷(2a2)=-3a4,所以选项A,C,D错误,故选B.
5.(2019山西,2,3分)下列运算正确的是 ( )A.2a+3a=5a2 B.(a+2b)2=a2+4b2C.a2·a3=a6 D.(-ab2)3=-a3b6
答案 D 2a+3a=5a,选项A错误;(a+2b)2=a2+4ab+4b2,选项B错误;a2·a3=a5,选项C错误;(-ab2)3=-a3b6,选项D 正确.故选D.
6.(2019陕西,5,3分)下列计算正确的是 ( )A.2a2·3a2=6a2 B.(-3a2b)2=6a4b2C.(a-b)2=a2-b2 D.-a2+2a2=a2
答案 D 2a2· 3a2 =6a4 ,选项A错误;(-3a2b)2=9a4b2,选项B错误;(a-b)2=a2-2ab+b2 ,选项C错误;-a2+2a2=a2 ,选 项D正确,故选D.
7.(2018内蒙古包头,5,3分)如果2xa+1y与x2yb-1是同类项,那么 的值是 ( )A. B. C.1 D.3
8.(2019湖北黄冈,10,3分)- x2y是 次单项式.
9.(2020吉林,15,5分)先化简,再求值:(a+1)2+a(1-a)-1,其中a= .
10.(2019甘肃兰州,18,5分)化简:a(1-2a)+2(a+1)(a-1).
解析 原式=a-2a2+2a2-2=a-2.
1.(2019贵州贵阳,3,3分)选择计算(-4xy2+3x2y)(4xy2+3x2y)的最佳方法是 ( )A.运用多项式乘多项式法则B.运用平方差公式C.运用单项式乘多项式法则D.运用完全平方公式
答案 B 本题属于多项式乘多项式问题,从两个多项式结构来看,3x2y相同,-4xy2与4xy2互为相反数,故可 以运用平方差公式计算,故选B.
2.(2020江西,7,3分)计算:(a-1)2= .
答案 a2-2a+1
解析 (a-1)2=a2-2a+1.
3.(2020辽宁营口,13,3分)(3 + )(3 - )= .
4.(2020新疆,17,7分)先化简,再求值:(x-2)2-4x(x-1)+(2x+1)(2x-1),其中x=- .
5.(2018吉林,15,5分)某同学化简a(a+2b)-(a+b)(a-b)出现了错误,解答过程如下:原式=a2+2ab-(a2-b2) (第一步)=a2+2ab-a2-b2 (第二步)=2ab-b2. (第三步)(1)该同学解答过程从第 步开始出错,错误原因是 ;(2)写出此题正确的解答过程.
解析 (1)二; (1分)去括号法则用错. (2分)(2)原式=a2+2ab-(a2-b2)=a2+2ab-a2+b2=2ab+b2. (5分)
1.(2020四川成都,11,4分)分解因式:x2+3x= .
答案 x(x+3)
解析 x2+3x=x(x+3).
2.(2020宁夏,9,3分)分解因式:3a2-6a+3= .
答案 3(a-1)2
解析 原式=3(a2-2a+1)=3(a-1)2.
3.(2019内蒙古呼和浩特,11,3分)因式分解:x2y-4y3= .
答案 y(x+2y)(x-2y)
解析 原式=y(x2-4y2)=y(x+2y)(x-2y).
4.(2019甘肃兰州,13,4分)因式分解:a3+2a2+a= .
答案 a(a+1)2
解析 a3+2a2+a=a(a2+2a+1)=a(a+1)2.
5.(2019云南,2,3分)分解因式:x2-2x+1= .
解析 x2-2x+1=(x-1)2.
6.(2019黑龙江齐齐哈尔,18(2),4分)因式分解:a2+1-2a+4(a-1).
解析 原式=(a-1)2+4(a-1)=(a-1)(a-1+4)=(a-1)(a+3).
1.(2018内蒙古包头,13,3分)若a-3b=2,3a-b=6,则b-a的值为 .
解析 由题意得(a-3b)+(3a-b)=8,∴4(a-b)=8,∴b-a=-2.
2.(2018吉林,9,3分)若a+b=4,ab=1,则a2b+ab2= .
解析 ∵a+b=4,ab=1,∴a2b+ab2=(a+b)ab=4×1=4.
3.(2020湖南长沙,14,3分)某数学老师在课外活动中做了一个有趣的游戏:首先发给A、B、C三个同学相 同数量的扑克牌(假定发到每个同学手中的扑克牌数量足够多),然后依次完成以下三个步骤:第一步,A同学拿出二张扑克牌给B同学;第二步,C同学拿出三张扑克牌给B同学;第三步,A同学手中此时有多少张扑克牌,B同学就拿出多少张扑克牌给A同学.请你确定,最终B同学手中剩余的扑克牌的张数为 .
解析 设开始发给每个同学的扑克牌的数量都是x,则第一步,A同学手中扑克牌的数量是x-2,B同学手中扑克牌的数量是x+2;第二步,B同学手中扑克牌的数量是x+2+3=x+5,C同学手中扑克牌的数量是x-3;第三步,A同学手中扑克牌的数量是2(x-2),B同学手中扑克牌的数量是x+5-(x-2)=7.故最终B同学手中剩余的扑克牌的张数是7.
4.(2019广东,16,4分)图1所示的图形是一个轴对称图形,且每个角都是直角,长度如图所示,小明按图2所 示的方法玩拼图游戏,两两相扣,相互间不留空隙,那么小明用9个这样的图形拼出来的图形的总长度是 (结果用含a、b的代数式表示). 图1 图2
解析 只有一个图形时的长度为a;当两个图形拼在一起时,长度为a+b;当三个图形拼在一起时,长度为a +2b;……,由此可发现规律,每增加一个图形,总长度增加b,所以9个图形拼在一起时总长度为a+8b.
疑难突破 解决规律探究型问题的一般思路是通过对所给的具体数据进行全面、仔细的观察,并分 析、比较,从中发现规律,得出一般性结论.
5.(2019河北,18,4分)如图,约定:上方相邻两数之和等于这两数下方箭头共同指向的数.示例: 即4+3=7. 则(1)用含x的式子表示m= ;(2)当y=-2时,n的值为 .
答案 (1)3x (2)1
解析 (1)根据约定可得x+2x=m,即m=3x.(2)根据约定及(1)可得n=2x+3,y=m+n=3x+2x+3=5x+3,当y=-2时,5x+3=-2,解得x=-1.所以n=2x+3=2×(-1)+3= 1.
1.(2020江西,2,3分)下列计算正确的是 ( )A.a3+a2=a5 B.a3-a2=aC.a3·a2=a6 D.a3÷a2=a
答案 D 对于A,B,a3,a2不是同类项,不能合并,故A、B不正确;对于C,a3·a2=a3+2=a5,故C不正确;对于D,a3÷ a2=a3-2=a,故D正确.
2.(2020广西北部湾经济区,4,3分)下列运算正确的是 ( )A.2x2+x2=2x4 B.x3·x3=2x3C.(x5)2=x7 D.2x7÷x5=2x2
答案 D 2x2+x2=3x2,故A错误;同底数幂相乘,底数不变,指数相加,x3·x3=x6,故B错误;幂的乘方,底数不变, 指数相乘,(x5)2=x10,故C错误;2x7÷x5=2x2,故D正确.故选D.
3.(2020山西,3,3分)下列运算正确的是 ( )A.3a+2a=5a2 B.-8a2÷(4a)=2aC.(-2a2)3=-8a6 D.4a3·3a2=12a6
答案 C 对于选项A,3a+2a=5a,故A错误;对于选项B,-8a2÷(4a)=-2a,故B错误;对于选项D,4a3·3a2=12a5, 故D错误,故选C.
4.(2019广东,4,3分)下列计算正确的是 ( )A.b6÷b3=b2 B.b3·b3=b9C.a2+a2=2a2 D.(a3)3=a6
答案 C 同底数幂相除,底数不变,指数相减,b6÷b3=b3,A选项错误;同底数幂相乘,底数不变,指数相加,b3· b3=b6,B选项错误;a2+a2=2a2,C选项正确;幂的乘方,底数不变,指数相乘,(a3)3=a9,D选项错误.故选C.
5.(2019山东潍坊,2,3分)下列运算正确的是 ( )A.3a×2a=6a B.a8÷a4=a2C.-3(a-1)=3-3a D. = a9
6.(2019河南,4,3分)下列计算正确的是 ( )A.2a+3a=6a B.(-3a)2=6a2C.(x-y)2=x2-y2 D.3 - =2
7.(2019安徽,2,4分)计算a3·(-a)的结果是 ( )A.a2 B.-a2 C.a4 D.-a4
答案 D a3·(-a)=-a4,故选D.
8.(2018山西,3,3分)下列运算正确的是 ( )A.(-a3)2=-a6 B.2a2+3a2=6a2C.2a2·a3=2a6 D. =-
9.(2017湖北武汉,3,3分)下列计算的结果是x5的为 ( )A.x10÷x2 B.x6-xC.x2·x3 D.(x2)3
答案 C 选项A,x10÷x2=x8,该选项不符合题意;选项B,x6与x不能合并,该选项不符合题意;选项C,x2·x3=x5, 该选项符合题意;选项D,(x2)3=x6,该选项不符合题意.故选C.
10.(2019天津,13,3分)计算x5·x的结果等于 .
解析 根据“同底数幂相乘,底数不变,指数相加”,可得x5·x=x6.
11.(2020湖北武汉,17,8分)计算:[a3·a5+(3a4)2]÷a2.
解析 原式=(a8+9a8)÷a2=10a8÷a2=10a6.
12.(2019吉林,15,5分)先化简,再求值:(a-1)2+a(a+2),其中a= .
13.(2019湖北武汉,17,8分)计算:(2x2)3-x2·x4.
解析 原式=8x6-x6=7x6.
1.(2018河北,4,3分)将9.52变形正确的是 ( )+(10+0.5)×(10-0.5)×10×0.5++9×0.5+0.52
答案 C 9.52=(10-0.5)2=102-2×10×0.5+0.52,故选C.
2.(2018湖北黄冈,10,3分)若a- = ,则a2+ 的值为 .
1.(2019山东潍坊,6,3分)下列因式分解正确的是 ( )A.3ax2-6ax=3(ax2-2ax)B.-x2+y2=(-x+y)(-x-y)C.a2+2ab+4b2=(a+2b)2D.-ax2+2ax-a=-a(x-1)2
答案 D A.3ax2-6ax=3ax(x-2),故此选项错误;B.-x2+y2=y2-x2=(y+x)(y-x),故此选项错误;C.a2+2ab+4b2无法 分解因式,故此选项错误;D.-ax2+2ax-a=-a(x-1)2,故此选项正确.故选D.
2.(2018安徽,5,4分)下列分解因式正确的是 ( )A.-x2+4x=-x(x+4)B.x2+xy+x=x(x+y)C.x(x-y)+y(y-x)=(x-y)2D.x2-4x+4=(x+2)(x-2)
答案 C 对于A,结果应是-x(x-4);对于B,结果应是x(x+y+1);对于D,结果应是(x-2)2,故选C.
3.(2020辽宁营口,11,3分)分解因式:ax2-2axy+ay2= .
答案 a(x-y)2
解析 ax2-2axy+ay2=a(x2-2xy+y2)=a(x-y)2.
4.(2020新疆,11,5分)分解因式:am2-an2= .
答案 a(m+n)(m-n)
解析 am2-an2=a(m2-n2)=a(m+n)(m-n).
5.(2019吉林,7,3分)分解因式:a2-1= .
答案 (a+1)(a-1)
解析 a2-1=(a+1)(a-1).
6.(2019浙江温州,11,5分)分解因式:m2+4m+4= .
解析 m2+4m+4=m2+2×2×m+22=(m+2)2.
7.(2019吉林长春,10,3分)分解因式:ab+2b= .
答案 b(a+2)
解析 提取公因式b,则ab+2b=b(a+2).
8.(2018内蒙古呼和浩特,11,3分)分解因式a2b-9b= .
答案 b(a+3)(a-3)
解析 a2b-9b=b(a2-9)=b(a+3)(a-3).
A组 2018—2020年模拟·基础题组时间:30分钟 分值:50分一、选择题(每小题3分,共21分)
1.(2020江西南昌一模,3)下列各式计算正确的是 ( )A.2a2-a2=a2 B.(3a)2=3a2C.-2(a-1)=-2a+1 D.(a+b)2=a2+b2
答案 A 2a2-a2=a2,所以A选项中的计算正确;(3a)2=9a2,所以B选项中的计算错误;-2(a-1)=-2a+2,所以C 选项中的计算错误;(a+b)2=a2+2ab+b2,所以D选项中的计算错误.故选A.
2.(2020湖北荆州4月模拟,6)若单项式-3x2y2m+n与2xm+ny4是同类项,则m2+2mn的算术平方根为 ( )A.0 B.2 C.-2 D.±2
3.(2020辽宁鞍山铁东一模,5)下列运算中正确的是 ( )A.3a+2b=5ab B.2a2+3a2=5a5C.a10÷a5=a2 D.(xy2)3=x3y6
答案 D 3a与2b不是同类项,不能合并,故A选项中的运算不正确;2a2+3a2=5a2,故B选项中的运算不正 确;a10÷a5=a5,故C选项中的运算不正确;(xy2)3=x3y6,故D选项中的运算正确.故选D.
4.(2019新疆喀什一模,5)计算(-2a2)·3a的结果是 ( )A.-6a2 B.-6a3 C.12a3 D.6a3
答案 B (-2a2)·3a=(-2×3)×(a2·a)=-6a3.故选B.
5.(2019内蒙古巴彦淖尔模拟,5)若单项式3x2m-1y5与单项式-5x3yn是同类项,则m,n的值分别为 ( )A.3,5 B.2,3 C.2,5 D.3,-2
答案 C ∵单项式3x2m-1y5与单项式-5x3yn是同类项,∴2m-1=3,n=5,∴m=2,故m,n的值分别为2,5.故选C.
6.(2018重庆江北质检,3)计算(-5x3y)2的结果是 ( )A.25x5y2 D.-10x6y2
答案 B (-5x3y)2=(-5)2·(x3)2·y2=25x6y2,故选B.
7.(2018湖北武汉武昌一模,5)若(x-2)(x+9)=x2+px+q,则p、q的值分别是 ( )A.7,18 B.7,-18C.-7,18 D.-7,-18
答案 B ∵(x-2)(x+9)=x2+7x-18=x2+px+q,∴p=7,q=-18.故选B.
二、填空题(每小题3分,共6分)8.(2020黑龙江绥化一模,11)分解因式:x3-6x2+9x= .
答案 x(x-3)2
解析 x3-6x2+9x=x(x2-6x+9)=x(x-3)2.
9.(2019云南曲靖一模,11)若x2-2x=3,则多项式2x2-4x+3的值为 .
解析 ∵x2-2x=3,∴原式=2(x2-2x)+3=6+3=9.
三、解答题(共23分)10.(2020江西南昌一模,13)化简:(2x+1)(2x-1)+(x+1)·(1-2x).
解析 (2x+1)(2x-1)+(x+1)(1-2x)=4x2-1+x-2x2+1-2x=2x2-x.
11.(2020甘肃兰州一诊,18)先化简,再求值:4a(a-1)-(1+2a)2,其中a=- .
12.(2019江西上饶广丰一模,13)已知x满足x2-4x-2=0,求(2x-3)2-(x+y)(x-y)-y2的值.
解析 原式=4x2-12x+9-x2+y2-y2=3x2-12x+9,∵x2-4x-2=0,∴x2-4x=2,∴原式=3(x2-4x)+9=3×2+9=6+9=15.
13.(2019吉林长春宽城一模,15)先化简,再求值:(2x-1)2+(x+2)(x-2)-4x(x-1),其中x= .
B组 2018—2020年模拟·提升题组时间:25分钟 分值:40分一、选择题(每小题3分,共15分)1.(2020海南琼海一模,2)下列运算正确的是 ( )A.a2+3a3=4a5 B.(a+b)2=a2+b2C.(b+a)(a-b)=a2-b2 D.(-3a3)2=6a6
答案 C a2与3a3不是同类项,不能合并,故A选项中的运算错误;(a+b)2=a2+2ab+b2,故B选项中的运算错 误;(b+a)(a-b)=a2-b2,故C选项中的运算正确;(-3a3)2=9a6,故D选项中的运算错误.故选C.
2.(2020湖北黄石模拟,5)化简5(2x-3)-4(3-2x)之后,可得下列哪一个结果 ( )A.2x-27 B.8x-15C.12x-15 D.18x-27
答案 D 5(2x-3)-4(3-2x)=5(2x-3)+4(2x-3)=9(2x-3)=18x-27.故选D.
3.(2019湖北仙桃模拟,7)若a+b=3,a2+b2=7,则ab等于 ( )A.2 B.1 C.-2 D.-1
答案 B ∵a+b=3,a2+b2=7,∴2ab=(a+b)2-(a2+b2)=32-7=2,∴ab=1.故选B.
4.(2018湖北孝感孝南一模,9)用棋子摆出下列一组图形: 按照这种规律摆下去,第n个图形用的棋子个数为 ( )A.3n B.6n C.3n+6 D.3n+3
答案 D ∵第1个图形需用棋子3+3=6个;第2个图形需用棋子3×2+3=9个;第3个图形需用棋子3×3+3=12个;……∴第n个图形需用棋子(3n+3)个.故选D.
5.(2019福建石狮一模,10)若(a-c+b)2=21,(a+c+b)2=2 019,则a2+b2+c2+2ab的值是 ( )A.1 020 B.1 998C.2 019 D.2 040
答案 A (a-c+b)2=a2+b2+c2-2ac-2bc+2ab=21①,(a+c+b)2=a2+b2+c2+2ac+2bc+2ab=2 019②,①+②,得2(a2+b2+c2)+4ab=2 040,所以a2+b2+c2+2ab=1 020.故选A.
二、填空题(每小题3分,共9分)6.(2020甘肃兰州一诊,13)分解因式:x3y-9xy= .
答案 xy(x+3)(x-3)
解析 x3y-9xy=xy(x2-9)=xy(x+3)(x-3).
7.(2020上海奉贤二模,7)计算:9a3b÷(3a2)= .
解析 原式=(9÷3)a3-2b=3ab.
8.(2019北京东城二模,11)如果x-y= ,那么代数式(x+2)2-4x+y(y-2x)的值是 .
三、解答题(共16分)9.(2020吉林长春一模,15)先化简,再求值:(a-1)2-2a·(a-1)+(2a+1)(2a-1),其中a= .
10.(2020吉林长春名校调研,15)先化简,再求值:b(b-2a)-(a-b)2,其中a=-3,b=- .
解析 原式=b2-2ab-a2+2ab-b2=-a2,当a=-3时,原式=-9.
2021年全国中考数学真题分类汇编--数与式:整式(试卷版): 这是一份2021年全国中考数学真题分类汇编--数与式:整式(试卷版),共4页。
2021年全国中考数学真题分类汇编--数与式:列代数式及求代数式的值(试卷版): 这是一份2021年全国中考数学真题分类汇编--数与式:列代数式及求代数式的值(试卷版),共5页。
2021年全国中考数学真题分类汇编--数与式:分式(试卷版): 这是一份2021年全国中考数学真题分类汇编--数与式:分式(试卷版),共4页。












