



2021版《5年中考3年模拟》全国版中考数学:§6.4 视图与投影
展开1.(2020山西,5,3分)泰勒斯是古希腊时期的思想家,科学家,哲学家,他最早提出了命题的证明,泰勒斯曾通 过测量同一时刻标杆的影长,标杆的高度,金字塔的影长,推算出金字塔的高度,这种测量原理,就是我们 所学的 ( )A.图形的平移 B.图形的旋转C.图形的轴对称 D.图形的相似
答案 D 根据在同一时刻的太阳光下物体的影长和物体的实际高度成比例,得到两个三角形相似,进 而推算出金字塔的高度,测量原理是图形的相似.故选D.
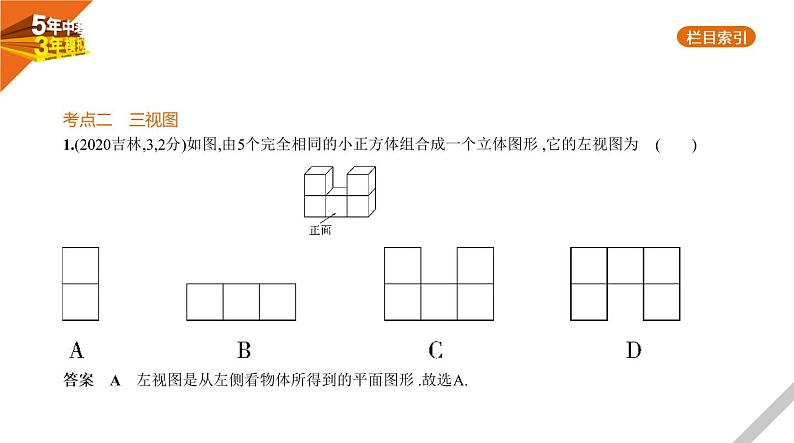
2.(2020贵州贵阳,6,3分)下列四幅图中,能表示两棵树在同一时刻太阳光下的影子的图是 ( )
答案 C 两棵树在同一时刻太阳光下的影子方向相同,树高和影长成正比,所以C选项正确.故选C.
3.(2019吉林,13,3分)在某一时刻,测得一根高为1.8 m的竹竿的影长为3 m,同时同地测得一栋楼的影长为 90 m,则这栋楼的高度为 m.
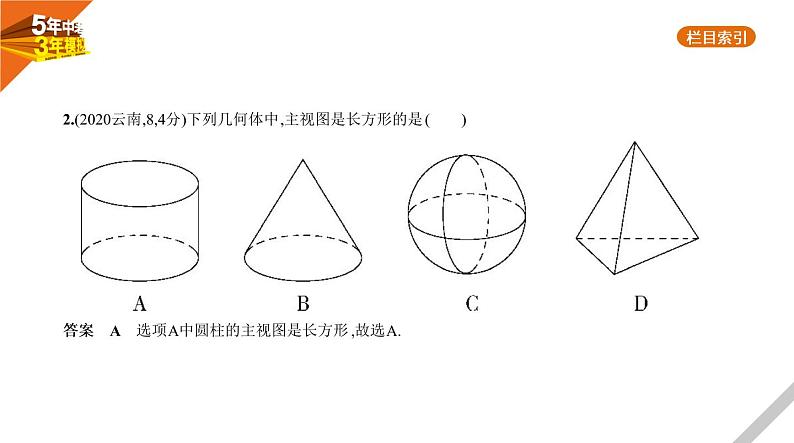
1.(2020吉林,3,2分)如图,由5个完全相同的小正方体组合成一个立体图形,它的左视图为 ( )
答案 A 左视图是从左侧看物体所得到的平面图形.故选A.
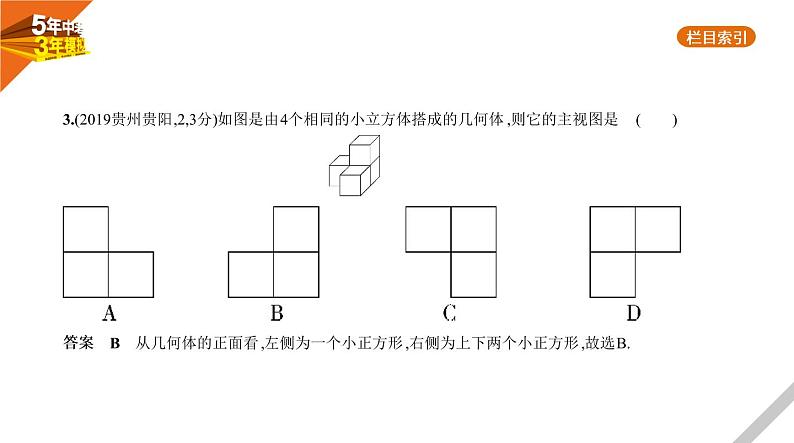
2.(2020云南,8,4分)下列几何体中,主视图是长方形的是( )
答案 A 选项A中圆柱的主视图是长方形,故选A.
3.(2019贵州贵阳,2,3分)如图是由4个相同的小立方体搭成的几何体,则它的主视图是 ( )
答案 B 从几何体的正面看,左侧为一个小正方形,右侧为上下两个小正方形,故选B.
4.(2019陕西,2,3分)如图是由两个正方体组成的几何体,则该几何体的俯视图为 ( )
答案 C 从上面看易得小正方体的俯视图落在大正方体的俯视图的内部的右上角,故选C.
5.(2019内蒙古呼和浩特,7,3分)如图是一个几何体的三视图,其中主视图与左视图完全一样,则这个几何 体的表面积是 ( ) A.80-2π B.80+4πC.80 D.80+6π
答案 B 根据几何体的三视图可知,该几何体为内部有一个圆孔的长方体,圆孔的直径为2,孔长与长方 体的高相等.长方体的长和宽均为4,高为3,所以该几何体的表面积为4×3×4+2×(42-π)+3×2π=80+4π,故 选B.
6.(2019江西,3,3分)如图是手提水果篮抽象的几何体,以箭头所指的方向为主视图方向,则它的俯视图为 ( )
答案 A 由俯视图的定义易知选A.
7.(2019黑龙江齐齐哈尔,6,3分)如图是由几个相同大小的小正方体搭建而成的几何体的主视图和俯视 图,则搭建这个几何体所需要的小正方体的个数至少为 ( ) A.5 B.6 C.7 D.8
答案 B 结合主视图和俯视图可知这个几何体共有2层,底层有4个小正方体,第2层最少有2个小正方 体.故搭建这个几何体的小正方体的个数最少是6.故选B.
8.(2019内蒙古包头,4,3分)一个圆柱体的三视图如图所示,若其俯视图为圆,则这个圆柱体的体积为 ( ) A.24 B.24π C.96 D.96π
答案 B 由左视图知底面圆的半径为2,∴圆柱体的体积为6×π×22=24π,故选B.
9.(2018黑龙江齐齐哈尔,13,3分)三棱柱的三视图如图所示,已知△EFG中,EF=8 cm,EG=12 cm,∠EFG=45 °,则AB的长为 cm.
10.(2020内蒙古呼和浩特,12,3分)一个几何体的三视图如图所示,则该几何体的表面积为 .
考点三 几何体的平面展开图
1.(2020江西,5,3分)如图所示,正方体的展开图为 ( )
答案 A 动手操作可知选A.
2.(2019山西,3,3分)某正方体的每个面上都有一个汉字,如图是它的一种展开图,那么在原正方体中,与 “点”字所在面相对的面上的汉字是 ( ) A.青 B.春 C.梦 D.想
答案 B 正方体的展开图中隔一行或隔一列的两个面可能是相对面,题图中的“点”与“春”所在面 隔着“亮”“青”一列,因此“点”与“春”所在面是相对面,故选B.
3.(2020山西,14,3分)如图是一张长12 cm,宽10 cm的矩形铁皮,将其剪去两个全等的正方形和两个全等的 矩形,剩余部分(阴影部分)可制成底面积是24 cm2的有盖的长方体铁盒.则剪去的正方形的边长为 cm.
考点一 投影(2016北京,14,3分)如图,小军、小珠之间的距离为2.7 m,他们在同一盏路灯下的影长分别为1.8 m,1.5 m. 已知小军、小珠的身高分别为1.8 m,1.5 m,则路灯的高为 m.
1.(2020宁夏,8,3分)图2是图1长方体的三视图,若用S表示面积,S主=a2,S左=a2+a,则S俯= ( ) A.a2+a B.2a2 C.a2+2a+1 D.2a2+a
答案 A 由长方体及三视图可知俯视图与左视图的面积相等,故选A.
2.(2020四川成都,2,3分)如图所示的几何体由4个大小相同的小立方块搭成,其左视图是 ( )
答案 D 从左面看到的是上下叠放在一起的两个小正方形,故选D.
3.(2020山西,4,3分)下列几何体都是由4个大小相同的小正方体组成的,其中主视图与左视图相同的几何 体是 ( )
4.(2020新疆,2,5分)如图所示,该几何体的俯视图是 ( )
答案 C 从上面往下看该几何体的俯视图是横放的四个正方形,符合题意的是C,故选C.
5.(2020湖北武汉,5,3分)下图是由4个相同的正方体组成的立体图形,它的左视图是 ( )
答案 A 从左边看,得到的图形是A中图形.
6.(2020云南昆明,7,4分)由5个完全相同的正方体组成的几何体的主视图是 ( )
答案 A 从正面看,可以看到从左到右共3列,第1、2列是一层,第3列是两层,所以选A.
7.(2020内蒙古包头,6,3分)如图,将小立方块①从6个大小相同的小立方块所搭的几何体中移走后,所得几 何体 ( ) A.主视图改变,左视图改变B.俯视图不变,左视图改变C.俯视图改变,左视图改变D.主视图不变,左视图不变
答案 C 主视图是从物体的正面看到的平面图形,把小立方块①移走后,主视图不发生改变;俯视图是 从物体的上面看到的平面图形,把小立方块①移走后,俯视图发生改变;左视图是从物体的左面看到的平 面图形,把小立方块①移走后,左视图发生改变,故选C.
8.(2019浙江温州,3,4分)某露天舞台如图所示,它的俯视图是 ( )
答案 B 俯视图是一个矩形里面有个小的矩形,边为实线且上边重合.故选B.
9.(2019河北,14,2分)图2是图1中长方体的三视图,若用S表示面积,且S主=x2+2x,S左=x2+x,则S俯= ( ) 图1 图2
A.x2+3x+2 B.x2+2C.x2+2x+1 D.2x2+3x
答案 A 由长方体的三视图可知长方体的高为x,根据S主=x2+2x可得长方体底面长方形的长为(x+2);根 据S左=x2+x可得长方体底面长方形的宽为(x+1),所以S俯=(x+2)(x+1)=x2+3x+2,故选A.
思路分析 首先根据长方体的主视图求出长方体底面长方形的长,进而根据长方体的左视图求出长方 体底面长方形的宽,两者的乘积即为长方体俯视图的面积.
10.(2019吉林,2,2分)如图,由6个相同的小正方体组合成一个立体图形,它的俯视图为 ( )
答案 D 从上面看这个立体图形,应该是一排并列的4个正方形.故选D.
11.(2019安徽,3,4分)一个由圆柱和长方体组成的几何体如图水平放置,它的俯视图是( )
答案 C 俯视图是一个正方形内有一个内切圆,且内切圆是看得见的,为实线,故选C.
12.(2019河南,5,3分)图①是由大小相同的小正方体搭成的几何体,将上层的小正方体平移后得到图②.关 于平移前后几何体的三视图,下列说法正确的是 ( ) A.主视图相同 B.左视图相同C.俯视图相同 D.三种视图都不相同
答案 C 根据题图①,图②中几何体的特征可知,它们的俯视图的形状均为“ ”,即平移前后几何体的俯视图相同.故选C.
13.(2018四川成都,3,3分)如图所示的正六棱柱的主视图是 ( )
答案 A 主视图是从正面看得到的图形,从正面看是左右相邻的3个矩形,中间的矩形面积较大,两边相 同,故选A.
1.(2018河南,3,3分)某正方体的每个面上都有一个汉字,如图是它的一种展开图,那么在原正方体中,与 “国”字所在面相对的面上的汉字是 ( ) A.厉 B.害 C.了 D.我
答案 D 根据正方体的展开图的特点可知,与“国”字所在面相对的面上的汉字是“我”,故选D.
2.(2017北京,3,3分)下图是某个几何体的展开图,该几何体是 ( ) A.三棱柱 B.圆锥 C.四棱柱 D.圆柱
答案 A 三棱柱上下底面为三角形,侧面是三个矩形;圆锥的展开图由扇形和圆组成;四棱柱上下底面 为四边形,侧面是四个矩形;圆柱的展开图由两个圆形和一个矩形组成.故选A.
A组 2018—2020年模拟·基础题组时间:30分钟 分值:45分一、选择题(每小题3分,共36分)
1.(2020甘肃兰州一诊,3)如图是由5个大小相同的正方体摆成的立体图形,它的左视图是 ( )
答案 C 从左往右看,得到从左往右2列正方形的个数依次为2,1,故选C.
2.(2020湖北武汉4月调考,5)已知某个几何体的主视图和俯视图如图,则该几何体可能为 ( )
3.(2020辽宁鞍山铁东一模,2)一个几何体的三视图如图所示,则这个几何体是 ( ) A.圆锥 B.长方体 C.圆柱 D.球
答案 B 由主视图与左视图都是等高的矩形,主视图与俯视图都是等长的矩形,得几何体是长方体,故 选B.
4.(2020内蒙古包头4月模拟,9)一个圆柱的三视图如图所示,则这个圆柱的体积为 ( ) A.24 B.24π C.96 D.96π
答案 B 由三视图可知圆柱的底面直径为4,∴底面半径r=2,又高h=6,∴V=πr2h=π·22×6=24π,故选B.
5.(2020天津河北3月模拟,5)如图所示的工件的俯视图是( )
答案 C 从上边看是两个同心圆,外圆是实线,内圆是虚线,故选C.
6.(2020山西晋中平遥一模,7)AB和DE是直立在水平地面上的两根立柱,AB=7米,某一时刻测得它在阳光 下的投影BC=4米,同时,测量出DE在阳光下的投影长为6米,则DE的长为 ( )A. 米 B. 米 C. 米 D. 米
答案 B 如图,设同一时刻DE在阳光下的投影为EF, 易知△ABC∽△DEF,∴ = ,又∵AB=7米,BC=4米,EF=6米,∴ = ,∴DE= 米.故选B.
7.(2019天津西青一模,5)如图是一个由6个相同的正方体组成的立体图形,它的主视图是 ( )
答案 D 从正面看一共是三列两层,左起第一列是1个小正方形,第二、三列各有2个小正方形,故选D.
8.(2019四川成都邛崃二诊,7)图中三视图对应的正三棱柱是 ( )
答案 A 由俯视图得正三棱柱两个底面在水平方向,由主视图得有一条侧棱在正前方,于是可判定A选 项正确.故选A.
9.(2019江西宜春高安一模,2)按图1放置的一个机器零件,若其主(正)视图如图2,则其俯视图是 ( )
答案 D 根据主视图可知,从上面看可得到左右相邻的3个矩形.故选D.
10.(2019黑龙江哈尔滨平房一模,5)下面两幅图是由几个小正方体搭成的几何体的主视图与俯视图,则搭 成这个几何体的小正方体有 ( ) A.3个 B.4个 C.5个 D.6个
答案 C 由俯视图可得该几何体最底层有4个小正方体,根据主视图可得该几何体第二层只有最右边 一列有1个小正方体,则搭成这个几何体的小正方体有4+1=5个.故选C.
11.(2019江西上饶广丰一模,4)我国古代数学著作《九章算术》中,将底面是直角三角形,且侧棱与底面 垂直的三棱柱称为“堑堵”,已知“堑堵”的三视图如图所示(网格图中每个小正方形的边长均为1),则 该“堑堵”的体积为( ) A.16+16 B.16+8 C.24+16 D.16
12.(2018贵州黔南州一模,8)如图是几个小立方块所搭成的几何体的俯视图,小正方形中的数字表示该位 置上小立方块的个数,则这个几何体的主视图是 ( )
二、解答题(共9分)13.(2019湖北咸宁咸安一模,18)如图所示是某个几何体从三种不同方向所看到的图形.(1)说出这个几何体的名称;(2)根据图中有关数据,求这个几何体的表面积.
B组 2018—2020年模拟·提升题组时间:30分钟 分值:36分一、选择题(每小题3分,共30分)1.(2020江西南昌一模,2)如图所示,把图1中正方体的一个角切割掉,形成了图2中的几何体,则图2中几何 体的俯视图是 ( )图1 图2
答案 C 从上面看题图2中几何体,看到的是正方形,且含有一条对角线,对角线从左上到右下,且为实 线,故选C.
2.(2020江西南昌二模,3)已知一种户外帐篷的实物图及其主视图如图所示,则它的左视图为 ( )
3.(2020黑龙江绥化一模,4)如图是由棱长为1的正方体搭成的某几何体的三视图,则图中棱长为1的正方 体的个数是 ( ) A.9 B.8 C.7 D.6
答案 B 该几何体共两层,由俯视图易得底层有6个正方体,由主视图和左视图得第二层有2个正方体, 故共有6+2=8个正方体,故选B.
4.(2020湖北黄石模拟,4)六个大小相同的正方体搭成的几何体如图所示,其俯视图是 ( )
答案 B 俯视图中共两行三列,从左到右分别有2,1,2个正方形,从前到后分别有2,3个正方形,故选B.
5.(2020四川成都青白江一诊,3)如图,夜晚路灯下有一排同样高的旗杆,离路灯越近,旗杆的影子 ( ) A.越长 B.越短C.一样长 D.随时间变化而变化
答案 B 如图,易得AB
7.(2019陕西西安工大附中一模,2)某校九年级(1)班在“迎中考百日誓师”活动中打算制作一个带有正 方体挂坠的倒计时牌挂在班级,正方体的每个面上分别书写“成功舍我其谁”六个字.如图是该班同学 设计的正方体挂坠的平面展开图,那么“我”字对面的字是 ( )A.舍 B.我 C.其 D.谁
答案 D 将该正方体表面展开图折叠成正方体知,“我”与“谁”是相对面,故选D.
8.(2019黑龙江哈尔滨松北一模,4)下列四个几何体中,左视图为圆的几何体是 ( )
答案 A A中球的左视图是圆,选项A正确;B中正方体的左视图是正方形,选项B错误;C中圆锥的左视 图是等腰三角形,选项C错误;D中圆柱的左视图是长方形,选项D错误.故选A.
9.(2019辽宁铁岭一模,2)桌上摆着一个由若干个相同正方体组成的几何体,其三视图如图所示,则组成此 几何体需要正方体的个数是 ( ) A.6 B.7 C.8 D.9
10.(2018天津南开一模,5)下面给出一个由7个相同的立方体叠成的几何体,如果用 表示1个立方体,用 表示两个立方体叠加,用 表示三个立方体叠加,那么从正前方观察该几何体,可画出的平面图形是 ( )
二、填空题(每小题3分,共6分)11.(2019黑龙江齐齐哈尔一模,12)如图是由几个相同的小正方体搭建而成的几何体的主视图和俯视图, 则搭建这个几何体所需要的小正方体至少有 个.
解析 由主视图和俯视图知,底层有5个小正方体,第二层至少有2个小正方体,第三层至少有1个,因此搭 成这个几何体的小正方体的个数最少是8.
12.(2018甘肃定西一模,13)如图是由一些完全相同的小正方体搭成的几何体的俯视图和左视图,则组成 这个几何体的小正方体的个数最少是 .
解析 根据几何体的左视图可得这个几何体共有3层,从俯视图中可以看出最底层小正方体的个数是4.(1)当从上往下数的第一层有1个小正方体,第二层有1个小正方体时,组成这个几何体的小正方体的个数 是1+1+4=6;(2)当从上往下数的第一层有1个小正方体,第二层有2个小正方体时,组成这个几何体的小正方体的个数 是1+2+4=7;(3)当从上往下数的第一层有2个小正方体,第二层有2个小正方体时,组成这个几何体的小正方体的个数 是2+2+4=8.综上可得,组成这个几何体的小正方体的个数是6或7或8.所以组成这个几何体的小正方体的个数最少是6.故答案为6.
一、选择题(每小题5分,共25分)
1.(2019辽宁本溪,2)下列图形中,既是轴对称图形又是中心对称图形的是 ( )
答案 B A选项中的图形不是中心对称图形,是轴对称图形,不符合题意;B选项中的图形既是轴对称图 形又是中心对称图形,符合题意;C选项中的图形是中心对称图形,不是轴对称图形,不符合题意;D选项中 的图形不是中心对称图形,是轴对称图形,不符合题意.故选B.
2.(2020山东潍坊,7)如图,点E是▱ABCD的边AD上的一点,且 = ,连接BE并延长交CD的延长线于点F.若DE=3,DF=4,则▱ABCD的周长为 ( ) A.21 B.28 C.34 D.42
3.(2019辽宁盘锦,7)如图,点P(8,6)在△ABC的边AC上,以原点O为位似中心,在第一象限内将△ABC的各 边缩小到原来的 ,得到△A'B'C',点P在A'C'上的对应点P'的坐标为 ( ) A.(4,3) B.(3,4)C.(5,3) D.(4,4)
答案 A ∵点P(8,6)在△ABC的边AC上,以原点O为位似中心,在第一象限内将△ABC的各边缩小到原 来的 ,得到△A'B'C',∴点P在A'C'上的对应点P'的坐标为(4,3).故选A.
4.(2020浙江杭州,4)如图,在△ABC中,∠C=90°,设∠A,∠B,∠C所对的边分别为a,b,c,则 ( ) A.c=bsin B B.b=csin B C.a=btan B D.b=ctan B
5.(2019湖北宜昌,15)如图,平面直角坐标系中,点B在第一象限,点A在x轴的正半轴上,∠AOB=∠B=30°, OA=2,将△AOB绕点O逆时针旋转90°,点B的对应点B'的坐标是 ( ) A.(-1,2+ ) B.(- ,3)C.(- ,2+ ) D.(-3, )
答案 B 如图,作B'H⊥y轴于H. ∵∠AOB=∠B=30°,∴OA=AB=2.又由旋转的性质可得OA'=A'B'=OA=2,∠A'B'O=∠A'OB'=30°,∴∠B'A'H=60°.∵B'H⊥A'H,∴∠A'B'H=30°,∴AH'= A'B'=1,B'H= ,∴OH=3,∴B'的坐标是(- ,3),故选B.
二、填空题(每小题5分,共20分)
6.(2019内蒙古赤峰,17)如图,一根竖直的木杆在离地面3.1 m处折断,木杆顶端落在地面上,且与地面成38 °角,则木杆折断之前高度约为 m.(参考数据:sin 38°≈0.62,cs 38°≈0.79,tan 38°≈0.78)
7.(2020黑龙江齐齐哈尔,14)如图是一个几何体的三视图,依据图中给出的数据,计算出这个几何体的侧 面积是 .
8.(2019广西柳州,17)如图,在△ABC中,sin B= ,tan C= ,AB=3,则AC的长为 .
9.(2019辽宁鞍山,16)如图,在矩形ABCD中,AB=5,BC=6,点M,N分别在AD,BC上,且AM= AD,BN= BC,E为直线BC上一动点,连接DE,将△DCE沿DE所在直线翻折得到△DC'E,当点C'恰好落在直线MN上时,CE的 长为 .
∵∠CDM=∠DCN=∠NMD=90°,∴四边形CDMN是矩形,∴CN=DM=4,∠CNM=90°,NE=CN-CE=4-CE.在Rt△C'NE中,∵NE2+C'N2=C'E2,∴(4-CE)2+22=CE2,解得CE= .当点C'落在NM的延长线上时,如图2.在Rt△C'MD中,C'M= = =3,∴C'N=MN+C'M=5+3=8.∵∠CDM=∠DCN=∠NMD=90°,∴四边形CDMN是矩形,∴CN=DM=4,∠CNM=∠MNE=90°,
NE=CE-CN=CE-4.在Rt△C'NE中,∵NE2+C'N2=C'E2,∴(CE-4)2+82=CE2,解得CE=10.故答案为 或10.
图1 图2
三、解答题(共4小题,共55分)10.(10分)(2019广西桂林,20)如图,在网格中,每个小正方形的边长均为1个单位长度,我们将小正方形的 顶点叫做格点,△ABC的三个顶点均在格点上.(1)将△ABC先向右平移6个单位长度,再向上平移3个单位长度,得到△A1B1C1,画出平移后的△A1B1C1;(2)建立适当的平面直角坐标系,使得点A的坐标为(-4,3);(3)在(2)的条件下,直接写出点A1的坐标.
解析 (1)△A1B1C1如图所示.(2)直角坐标系如图所示. (3)A1(2,6).
11.(15分)(2020浙江杭州,19)如图,在△ABC中,点D,E,F分别在AB,BC,AC边上,DE∥AC,EF∥AB.(1)求证:△BDE∽△EFC;(2)设 = .①若BC=12,求线段BE的长;②若△EFC的面积是20,求△ABC的面积.
解析 (1)证明:因为DE∥AC,所以∠BED=∠C,又因为EF∥AB,所以∠B=∠FEC,所以△BDE∽△EFC.(2)①因为EF∥AB,所以 = = .因为BC=12,所以 = ,所以BE=4.②因为EF∥AB,所以△EFC∽△BAC,因为 = ,所以 = .设△EFC的面积为S1,△ABC的面积为S,所以 = .因为S1=20,所以S=45,所以△ABC的面积是45.
解后反思 由相似三角形的判定定理来判定相似.以相似三角形为背景求某些线段的长及面积常常运 用相似三角形的性质求解.相似三角形的性质包括:(1)对应角相等;(2)对应边成比例;(3)周长比等于相似 比;(4)面积比等于相似比的平方.解本题的关键是灵活运用相似三角形的性质.
12.(15分)(2020贵州贵阳,21)脱贫攻坚工作让老百姓过上了幸福的生活.图①是政府给贫困户新建的房 屋,图②是房屋的侧面示意图,它是一个轴对称图形,对称轴是房屋的高AB所在的直线.为了测量房屋的 高度,在地面上C点测得屋顶A的仰角为35°,此时地面上C点、屋檐上E点、屋顶上A点三点恰好共线,继 续向房屋方向走8 m到达点D时,又测得屋檐E点的仰角为60°,房屋的顶层横梁EF=12 m,EF∥CB,AB交 EF于点G(点C,D,B在同一水平线上).(参考数据:sin 35°≈0.6,cs 35°≈0.8,tan 35°≈0.7, ≈1.7)(1)求屋顶到横梁的距离AG;(2)求房屋的高AB(结果精确到1 m).
解析 (1)∵房屋的侧面示意图是轴对称图形,AB所在直线是对称轴,EF∥CB,∴AG⊥EF,EG= EF=6,∠AEG=∠ACB=35°.在Rt△AGE中,∠AGE=90°,∠AEG=35°,∵tan∠AEG= ,EG=6,tan 35°≈0.7,∴AG=6tan 35°≈4.2.答:屋顶到横梁的距离AG约是4.2米.(2)过点E作EH⊥CB于点H,设EH=x米,在Rt△EDH中,∠EHD=90°,∠EDH=60°,∵tan∠EDH= ,∴DH= .在Rt△ECH中,∠EHC=90°,∠ECH=35°,∵tan∠ECH= ,∴CH= .
∵CH-DH=CD=8,∴ - =8,∵tan 35°≈0.7, ≈1.7,∴x≈9.52.∴AB=AG+BG=4.2+9.52=13.72≈14.答:房屋的高AB约是14米.
13.(15分)(2019黑龙江绥化,28)如图①,在正方形ABCD中,AB=6,M为对角线BD上任意一点(不与B、D重 合),连接CM,过点M作MN⊥CM,交线段AB于点N.(1)求证:MN=MC;(2)若DM∶DB=2∶5,求证:AN=4BN;(3)如图②,连接NC交BD于点G.若BG∶MG=3∶5,求NG·CG的值.
解析 (1)如图,过M分别作ME∥AB交BC于E,MF∥BC交AB于F, 则四边形BEMF是平行四边形.∵四边形ABCD是正方形,∴∠ABC=90°,∠ABD=∠CBD=∠BME=45°,∴ME=BE,∴平行四边形BEMF是正方形,∴ME=MF.∵CM⊥MN,∴∠CMN=90°.∵∠FME=90°,∴∠CME=∠FMN,
又∠MEC=∠MFN=90°,∴△MFN≌△MEC(ASA),∴MN=MC.(2)由(1)得FM∥AD,EM∥CD,∴ = = = ,∴AF=2.4,CE=2.4.∵△MFN≌△MEC,∴FN=EC=2.4,∴AN=4.8,BN=6-4.8=1.2,∴AN=4BN.(3)如图,把△DMC绕点C逆时针旋转90°得到△BHC,连接GH.
由旋转的性质可得△DMC≌△BHC,∠BCD=90°,∴MC=HC,DM=BH,∠CDM=∠CBH=45°,∠DCM=∠BCH,∴∠MBH=90°,∠MCH=90°.∵MC=MN,MC⊥MN,∴△MNC是等腰直角三角形,∴∠MCN=∠MNC=45°,∴∠NCH=45°,∴△MCG≌△HCG(SAS),
中考数学模拟汇编一45投影与视图: 这是一份中考数学模拟汇编一45投影与视图,共18页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
中考数学模拟汇编二45投影与视图: 这是一份中考数学模拟汇编二45投影与视图,共8页。试卷主要包含了选择题,填空题等内容,欢迎下载使用。
初中数学中考复习 考点33 视图与投影(解析版): 这是一份初中数学中考复习 考点33 视图与投影(解析版),共16页。












