人教版八年级下册19.3 课题学习 选择方案精品课件ppt

这是一份人教版八年级下册19.3 课题学习 选择方案精品课件ppt，共28页。PPT课件主要包含了学习目标，课堂导入，新知探究，随堂练习，课堂小结，拓展提升等内容，欢迎下载使用。

1.会建立实际问题的数学模型，将实际问题转化为数学问题.2.会综合运用一次函数的图象和性质、方程（组）和不等式（组）等知识解决方案设计问题.
做一件事情，有时有不同的实施方案.比较这些方案，从中选择最佳方案作为行动计划，是非常必要的.在选择方案时，往往需要从数学角度进行分析，涉及变量的问题常用到函数.
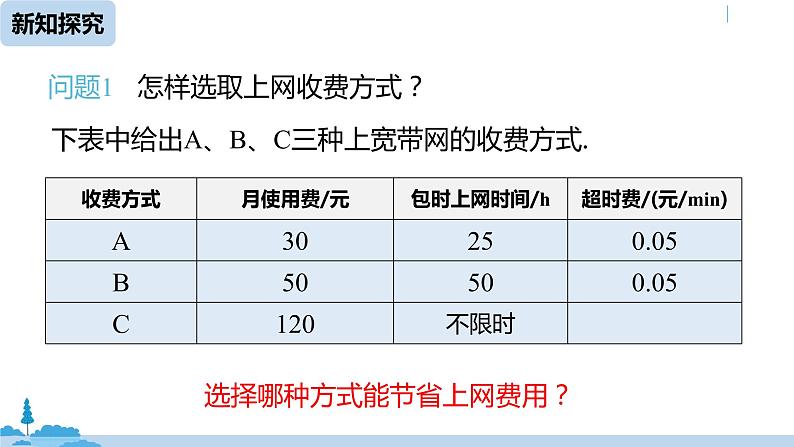
问题1 怎样选取上网收费方式？
下表中给出A、B、C三种上宽带网的收费方式.
选择哪种方式能节省上网费用？
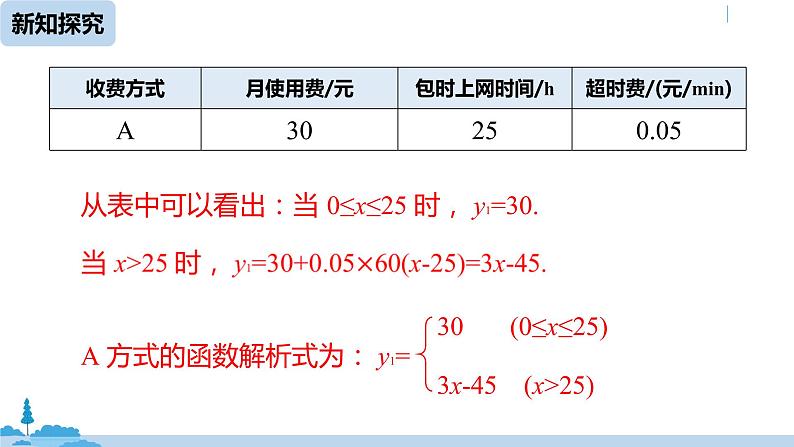
思考1 上表中哪些方式上网费用是变化的，哪些是不变的？
A、B 方式的上网费用是随着时间的变化而变化的，C 方式的上网费用是不变的.
思考2 A、B 方式中上网费用是怎样构成的？
A、B 方式的上网费用是由月使用费用 + 超时费用构成的.
思考3 设上网时间为 x h，则 A、B 方式的上网费用 y1、y2 都是关于 x 的函数，比较哪种方式更优惠应该怎么比较？
x 代表上网时间，则需要比较在 x>0 的范围内，考虑何时： （1） y1>y2 （2）y1=y2 （3）y1从表中可以看出：当 0≤x≤25 时， y1=30.
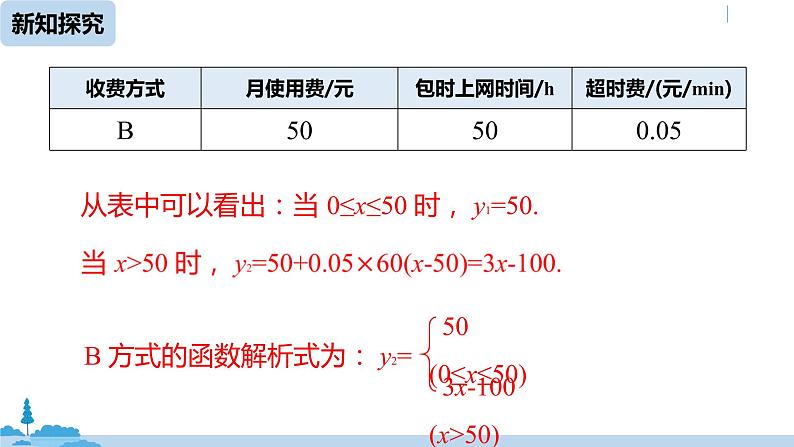
从表中可以看出：当 0≤x≤50 时， y1=50.
从表中可以看出：无论上网时间多久，每月只用交一次费用即可.
C 方式的函数解析式为： y3= 120 (x≥0)
在同一坐标系中分别画出A、B、C三种方式的函数图象，并进行比较：
从图中可以看出：在直线 l1 的左侧，A 方式最省钱.
从图中可以看出：在直线 l1和直线 l2 之间，B 方式最省钱.
从图中可以看出：在直线 l2的右侧，C 方式最省钱.
问题2 怎样租车？
某学校计划在总费用 2300 元的限额内，租用汽车送 234 名学生和 6 名教师集体外出活动，每辆汽车上至少要有 1 名教师.现有甲、乙两种大客车，它们的载客量和租金如表所示：
思考1 租车方案有哪几种？
①单独租用甲种客车；②单独租用乙种客车；③同时租用甲种客车和乙种客车.
思考2 如果甲、乙都租，你能确定合租车辆的范围吗？
汽车总数不能小于 6 辆，不能超过 8 辆.
设租用甲种客车 x 辆，则租用乙种客车 (6-x) 辆.租车总费用为 y 元.
从人数上：6 名教师和 234 名学生共计 240 人，所以甲种客车和乙种客车总共的载客量要≥240.
从费用上：学校计划的费用是 2300 元，所以甲种客车和乙种客车总共的费用要≤2300.
方案一：当 x=4 时，即需用甲种客车 4 辆，乙种客车 2 辆.
方案二：当 x=5 时，即需用甲种客车 5 辆，乙种客车 1 辆.
通过一次函数的性质来判断：
用一次函数选择最佳方案的一般步骤
1.析：分析题意，弄清数量关系.
2.列：列出函数解析式、不等式或方程.
3.求：求出自变量取不同值对应的函数值的大小，或函数的最大（小）值.
4.选：结合实际需要选择最佳方案.
一家电信公司提供两种手机月通话方式供用户选择，其中一种有月租，另一种无月租，这两种收费方式的通话费用 y（元）与通话时间 x（分钟）之间的函数关系如图所示.请你判断下列叙述是否正确.
（1）l1描述的是无月租费用的收费方式.
（2）l2描述的是有月租费用的收费方式.
（3）当每月的通话时间超过 400 分钟的时候选择有月租的收费方式更省钱.
正确，超过 400 分钟后， l1 方式的费用小于 l2 方式的费用.
学校计划为“我和我的祖国”演讲比赛购买奖品.已知购买 3 个 A 奖品和 2 个 B 奖品共需 120 元；购买 5 个 A 奖品和 4个 B 奖品共需 210 元.
（1）求 A、B 两种奖品的单价；
解：（1）设 A 奖品的单价为 x 元，B 奖品的单价为 y 元.
所以 A 奖品的单价为 30 元，B 奖品的单价为 15 元.