人教版八年级下册18.1 平行四边形综合与测试优秀课件ppt

这是一份人教版八年级下册18.1 平行四边形综合与测试优秀课件ppt，共49页。PPT课件主要包含了平行四边形的性质，练一练等内容，欢迎下载使用。
两组对边分别平行的四边形是平行四边形。
平行四边形的两组对边分别相等
两组对边分别相等的四边形是平行四边形。
平行四边形两组对角分别相等
两组对角分别相等的四边形是平行四边形。
平行四边形对角线互相平分
对角线互相平分的四边形是平行四边形。
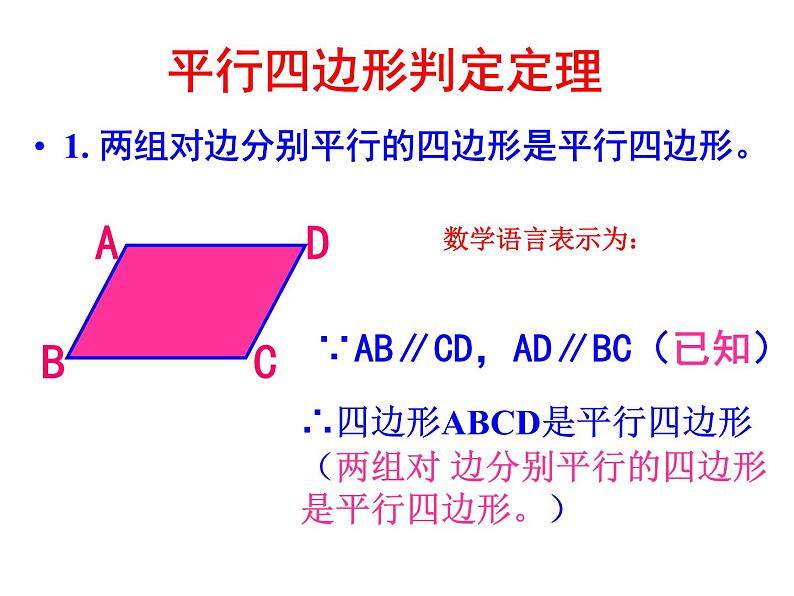
1. 两组对边分别平行的四边形是平行四边形。
∵AB∥CD，AD∥BC（已知）
∴四边形ABCD是平行四边形（两组对 边分别平行的四边形是平行四边形。）
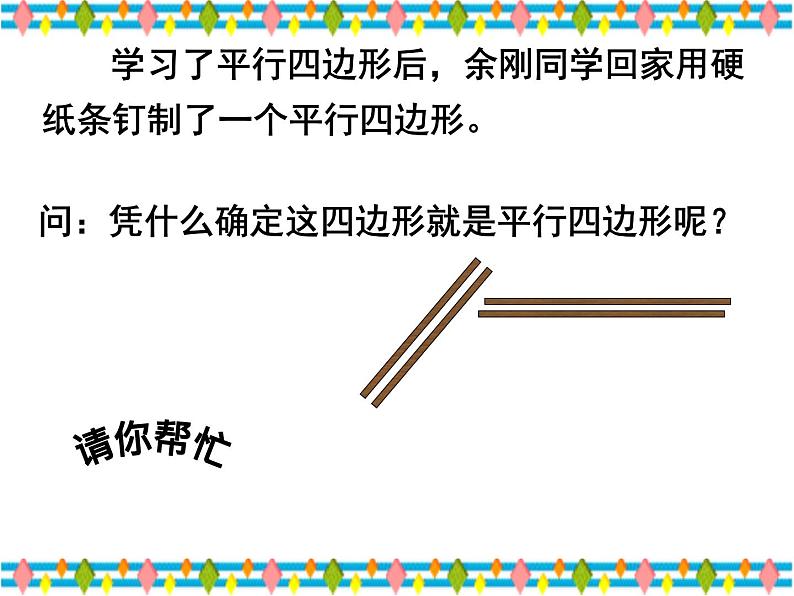
学习了平行四边形后，余刚同学回家用硬纸条钉制了一个平行四边形。
问：凭什么确定这四边形就是平行四边形呢？
猜想：两组对边分别相等的四 边形是平行四边形。
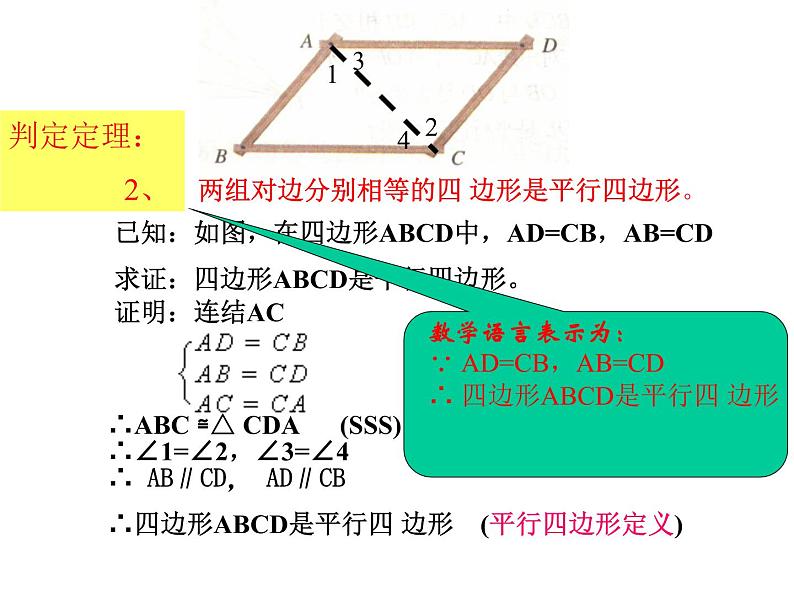
已知：如图，在四边形ABCD中，AD=CB，AB=CD
求证：四边形ABCD是平行四边形。
∴ABC ≌△ CDA (SSS)
∴∠1=∠2，∠3=∠4
∴ AB∥CD， AD∥CB
∴四边形ABCD是平行四 边形 (平行四边形定义)
判定定理： 2、
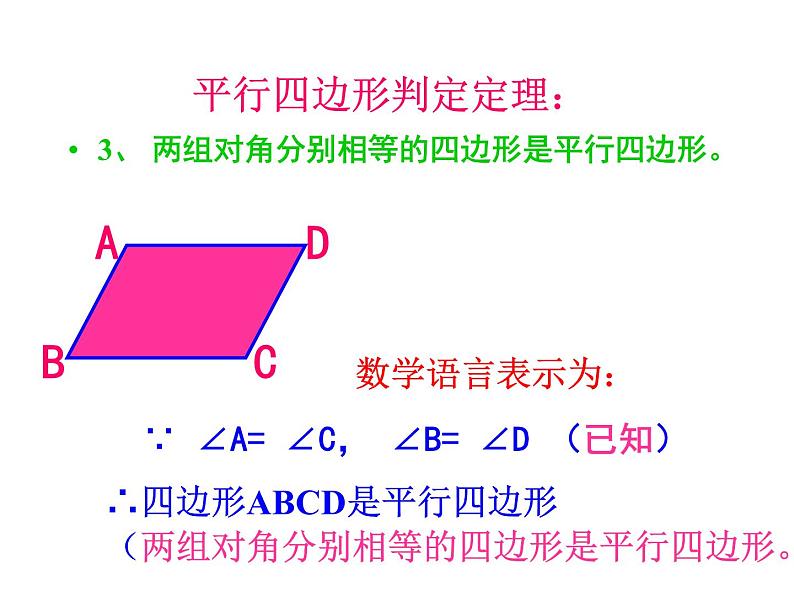
3、 两组对角分别相等的四边形是平行四边形。
∵ ∠A= ∠C， ∠B= ∠D （已知）
∴四边形ABCD是平行四边形（两组对角分别相等的四边形是平行四边形。）
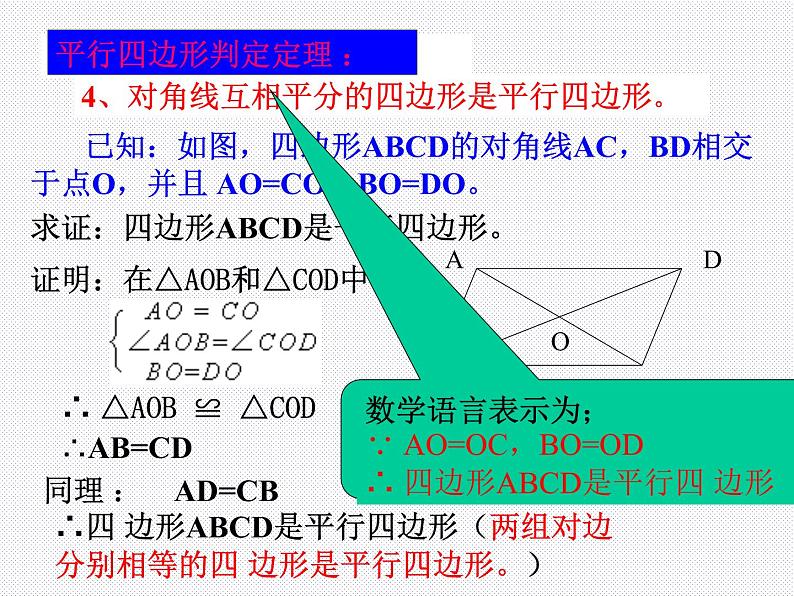
4、对角线互相平分的四边形是平行四边形。
已知：如图，四边形ABCD的对角线AC，BD相交于点O，并且 AO=CO，BO=DO。
证明：在△AOB和△COD中
∴ △AOB ≌ △COD (SAS)
同理 ： AD=CB
∴四 边形ABCD是平行四边形（两组对边分别相等的四 边形是平行四边形。）
你能根据上述判定定理证明
平行四边形判定定理 ：
1、两组对边分别平行的四边形是平行四边形。（定义）
平行四边形的判定方法（P87）
2、两组对边分别相等的四边形是平行四边形。（判定定理）
4、对角线互相平分的四边形是平行四边形。 （判定定理）
3、两组对角分别相等的四边形是平行四边形（判定定理）
例1： 已知：如图 ，E、F是平行四边形ABCD对角线AC 上的两点，并且 AE=CF。 求证：四边形BFDE是平行四边形。
证明：连结BD，交AC于点O
∵四边形ABCD是平行四边形
∴AO=CO ，BO=DO
∴四边形BFDE是平行四边形 (对角线互相平分的四边形是平行四边形)
上的两点,且E.F是OA.OC的中点.
上的两点,且DE⊥OA.BF⊥OC.
某同学说：“只要给我一把尺，我就能判断一个四边形是否为平行四边形。” 请你说出该同学是怎样判断的。
是非题 1、有三个角是直角的四边形是平行四边形
2、有两组对边分别相等的四边形是平行四边形
3、两条对角线相等的四边形是平行四边形
4、任意相邻两个角都互补的四边形是平行四边形
5、一组对边平行，另一组对边相等的四边形一定是平行四边形
6、有两条边相等，并且另外的两条边也相等的四边形一定是平行四边形
在平行四边形ABCD中，E、F为对角线BD上两点，且＿＿＿＿＿＿，请添加一个条件，使四边形AECF是平行四边形。 　　　
通过了本节课学习,你有哪些收获?
18.1.2 平行四边形的判定二
将一根木棒从AB平移到DC，AB与DC之间的位置关系、数量关系？
四边形ABCD是什么样的图形？
猜测：一组对边平行且相等的四边 形是平行四边形
猜测：一组对边平行且相等的四边形是平行四边形
已知：四边形ABCD中 AB∥CD， AB＝CD
求证：四边形ABCD是平行 四边形
判定方法（5）(P88)
一组对边平行且相等（记作：“ ”） 的四边形是平行四边形
归纳：平行四边形判定方法
(1) AB∥CD, BC∥AD
(2) AB=CD，BC=AD
(4) ∠A= ∠C ， ∠ B=∠ D
(3) AO=OC, BO=OD
(5) AB∥CD,AB=CD
1、什么叫三角形的中线？有几条？
2、三角形的中线有哪些性质？
　　连结三角形的顶点和对边中点的线段叫三角形的中线.
①三角形的每一条中线把三角形的面积平分.②三角形的中线相交于同一点.……
P89连结三角形两边中点的线段叫三角形的中位线。
1、一个三角形有几条中位线？
2、这三条中位线把三角形分成几个三角形？
DE是△ABC的中位线
三角形的中位线与三角形的中线有什么区别？
中位线是两条边中点的连线，而中线是一个顶点和对边中点的连线。
三角形的中位线具有怎样的性质呢？
即DE与BC有什么样的位置关系和数量关系？
1、如图在等边△ABC中，AD=BD，AE=EC，
△ADE是什么三角形？
DE与BC有什么样的位置关系和数量关系？
一般的三角形的中位线与第三边有什么样的位置关系和数量关系呢？
DE是△ABC的什么线？
猜想：三角形的中位线平行于第三边，并且等于第三边的一半。
∵DE=EF 、∠AED=∠CEF 、AE=EC∴△ADE ≌ △CFE
证明：如 图，延 长DE 到 F，使EF=DE ，连 结CF.
∴AD=FC 、∠A=∠ECF∴AB∥FC
又AD=DB ∴BD∥ CF且 BD =CF所以 ，四边形BCFD是平行四边形
∴DF∥BC，DF＝BC
P88例4已知在△ABC 中，DE是△ABC 的中位线 求证：DE ∥ BC，且DE= BC 。
P88已知：如图，点D、E分别是△ABC的边AB、AC的中点，求证DE∥BC且DE= BC
证明：延长DE到F,使EF=DE,连接FC、DC、AF.
∴四边形ADCF是平行四边形
∴四边形DBCF是平行四边形
CF∥DA，CF=DA
∴CF∥BD，CF=BD
DF∥BC，DF=BC
三角形的中位线的定理（P89）
三角形的中位线平行于第三边，并且等于它的一半
1.△ABC中,D、E分别是AB、AC的中点， BC=10cm，则DE=______.
2. △ABC中,D、E分别是AB、AC的中点，∠A=50°, ∠B=70°,则∠AED=_____.
例1：口答 （1）三角形的周长为18cm，这个三角形的三条中位线围成三角形的周长是多少？为什么？
（2）如图，E是平行四边形ABCD的AB边上的中点，且AD=10cm，那么OE= cm。
（3）如图：如果AD= AC，AE= AB，DE=2cm，那么BC= cm。
（4）在△ABC中，E、F、G、H分别为AC、CD、 BD、 AB的中点，若AD=3，BC=8，则四边形EFGH的周长是 。
作业：新支点P61 第二课时
平行四边形的判定三(P89)
1、三角形中位线的定义
连接三角形两边中点的线段叫做三角形的中位线
三角形的中位线平行于三角形的第三边，且等于第三边的一半
例2：如图，点D、E、F分别是△ABC的边AB、BC、CA的中点，求证：（1）∠A= ∠DEF （2）四边形AFED的周长等于AB+AC
（1）图中有几个平行四边形？
（2）这四个三角形有什么关系？
例3：已知，如图AD是△ABC的中线，EF是中位线，求证：AD与EF互相平分
例4：求证顺次连结四边形各边中点所得的四边形是平行四边形。
已知：E、F、G、H分别是四边形ABCD中AB、 BC、CD、DA的中点。求证：EFGH是平行四边形。
任意四边形四边中点连线所得的四边形一定是平行四边形。
例5：如图，任意四边形ABCD，E、F分别是AD、BC的中点，试说明EF与两条对角线AC、BD有什么关系。
任意四边形一组对边中点的连线段小于两条对角线和的一半。
例6：已知，四边形ABCD中，F是AB的中点，E是CD的中点，求证：EF　 （AD+BC）
（1）点G不在EF上时
如图，l1 // l2 ， 线段AB//CD//EF, 且点A、C、E在l1上，B、D、F在l2上，则AB、CD、EF的长短相等吗？为什么？
夹在两平行线间的平行线段相等。（补充）
如图，l1 // l2 ，点A、C、E在l1上，线段AB、CD、EF都垂直与l2 ，垂足分别为B、D、F，则AB、CD、EF的长短相等吗？为什么？
一条直线上的任一点到另一条直线的距离，叫做这两条平行线间的距离。（P89）
平行线间的距离处处相等（P89）
它与点与点的距离、点到直线的距离的联系与区别
如图，在平行四边形ABCD的一组对边AD、BC上截取EF＝MN，连接EM、FN，EM和FN有怎样的关系？为什么？
课后巩固1．（填空）一个三角形的周长是135cm，过三角形各顶点作对边的平行线，则这三条平行线所组成的三角形的周长是 cm．2．（填空）已知：△ABC中，点D、E、F分别是△ABC三边的中点，如果△DEF的周长是12cm，那么△ABC的周长是 cm．
3、两条平行线间的距离
一条直线上的任一点到另一条直线的距离，叫做这两条平行线间的距离
平行线间的距离处处相等