初中数学人教版八年级下册17.1 勾股定理完美版ppt课件

这是一份初中数学人教版八年级下册17.1 勾股定理完美版ppt课件，共60页。PPT课件主要包含了a2+b2c2，有趣的总统证法，自主评价等内容，欢迎下载使用。

斯学派，他们首先发现了勾股定理，因此
在国外人们通常称勾股定理为毕达哥拉斯
年希腊曾经发行了一枚纪念票。
定理。为了纪念毕达哥拉斯学派，1955
两千多年前，古希腊有个毕达哥拉斯学派，他们首先发现了勾股定理，因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派，1955年希腊曾经发行了一枚纪念邮票。
相传，毕达哥拉斯发现这一定理时，曾宰牛百头，广设盛宴，表示庆贺，对这个定理的重视可想而知。
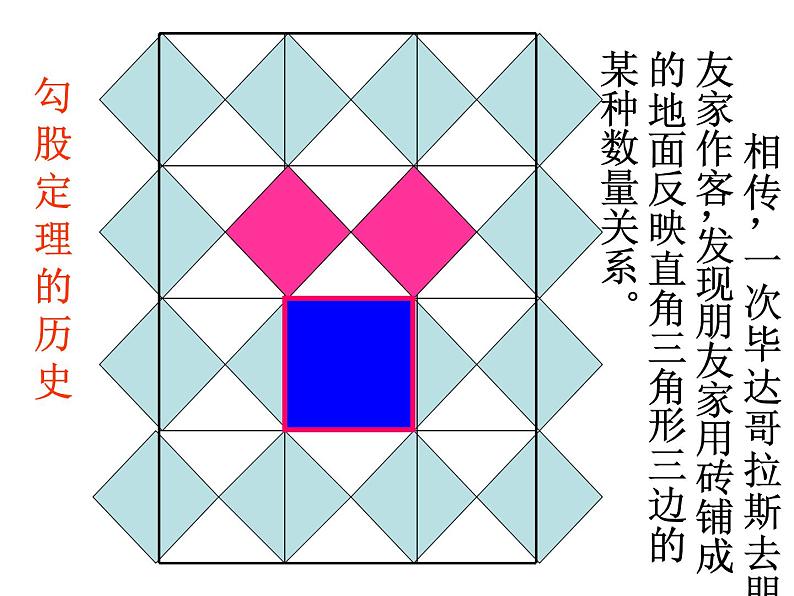
相传，一次毕达哥拉斯去朋友家作客，发现朋友家用砖铺成的地面反映直角三角形三边的某种数量关系。
我国是最早了解勾股定理的国家之一。早在三千多年前，周朝数学家商高就提出，将一根直尺折成一个直角，如果勾等于三，股等于四，那么弦就等于五，即“勾三、股四、弦五”，它被记载于我国古代著名的数学著作《周髀算经》中。
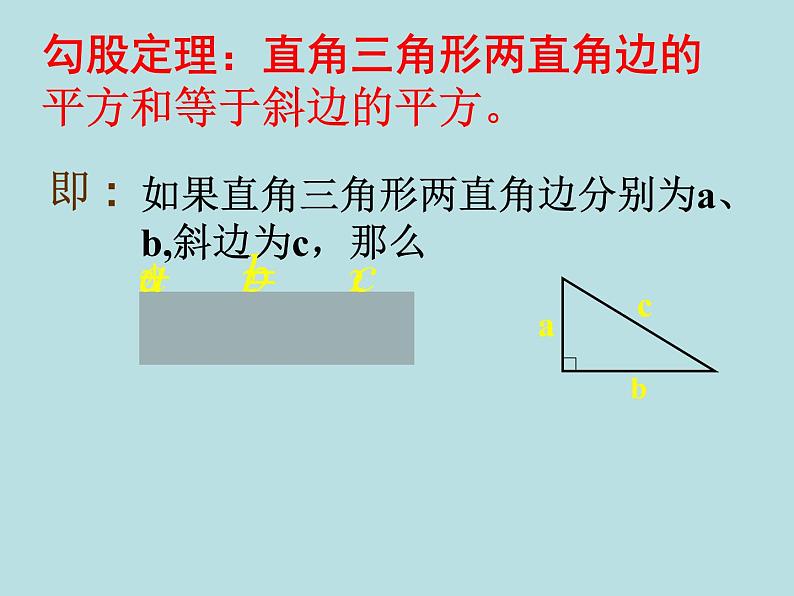
勾股定理：直角三角形两直角边的平方和等于斜边的平方。
如果直角三角形两直角边分别为a、b,斜边为c，那么
那么勾股定理是如何证明的呢？
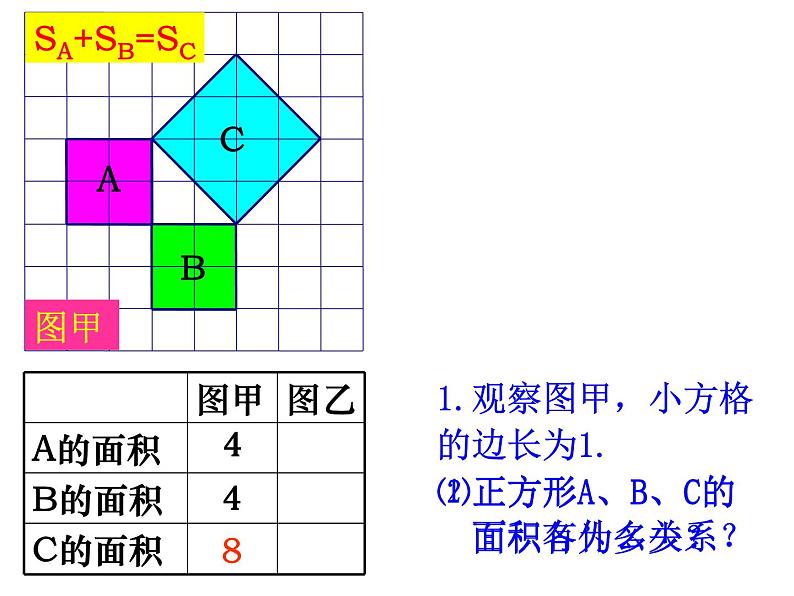
1.观察图甲，小方格的边长为1.⑴正方形A、B、C的　面积各为多少？
⑵正方形A、B、C的 面积有什么关系？
2.观察图乙，小方格的边长为1.⑴正方形A、B、C的　面积各为多少？
2.观察图乙，小方格的边长为1.
3.猜想a、b、c 之间的关系？
∵ S大正方形=4×S直角三角形+ S小正方形
∴a2 +b2 =c2
如果直角三角形两直角边分别为a， b，斜边为c，那么
勾股定理是几何中一个非常重要的定理，自古以来人们进行了大量的长期的研究，目前世界上可查到的证明方法有三百多种。
我国有记载的最早勾股定理的证明，是三国时，我国古代数学家赵爽在他所著的《勾股圆方图注》中，用四个全等的直角三角形拼成一个中空的正方形来证明的。
每个直角三角形的面积叫朱实，中间的正方形面积叫黄实，大正方形面积叫弦实，这个图也叫弦图。
美国第二十任总统伽菲尔德的证法在数学史上被传为佳话人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明，就把这一证法称为“总统”证法。
c2 = a2 + b2
直角三角形两直角边的平方和等于斜边的平方。
结论：在直角三角形中，已知两边可以求第三边.
例1 在Rt△ABC中,BC=24,AC=7,求AB的长.
如果将题目变为： 在Rt△ABC中,AB=41, BC=40,求AC的长呢？
∵ Rt△ABC中, ∠C是直角
AC2+BC2=AB2
1 .在Rt△ABC中，∠Ｃ=90°. (1) 已知：a=6，ｂ=8，求c；　 (2) 已知：a=40，c=41，求b； (3) 已知：c=13，b=5，求a； (4) 已知: a:b=3:4, c=15,求a、b.
(1)在直角三角形中,已知两边,可求第三边;(2)可用勾股定理建立方程.
2、已知：Rt△ＡBC中，AB＝４，AC＝３,则BC的长为 .
3、如图,折叠长方形的一边，使点D落在BC边上的点F处，若AB=8，AD=10.求：EC的长.
4、如图， △ABC 中，CD⊥AB于D求证：AC2 – BC2 = AB ·（AD -BD）
1、在Rt△ABC中，∠C=90°, (1)已知a=3,b=4,则c=______ (2)已知a=6,c=10,则b=_____ (3)已知a=2,b=4,则c=______2、直角三角形的两条边长分别为 5、12，则第三边长为 .
4、如图，在△ABC中，AB=AC，D点在CB延长线上，求证：AD2-AB2=BD·CD
如图，在△ABC中，AB=AC，D点在CB延长线上，求证：AD2-AB2=BD·CD
∵AB=AC，∴BE=CE
AD2=AE2+DE2
AB2=AE2+BE2
∴ AD2-AB2=(AE2+DE2)-(AE2+BE2)
= (DE+BE)·( DE- BE)
= (DE+CE)·( DE- BE)
探究1、求下列各边长：
探究2、求下列各边长：
练习1、在Rt△ABC中，∠Ｃ=90°， AB=10
(1) ∠A=30°，求：BC、AC(2) ∠A=45°，求：BC、AC
练习2、一个3m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?
探究3、在数轴上画出表示 的点。
利用勾股定理作出长为 的线段.
如图,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是( ) (π的值取3)
如图,正四棱柱的底面边长为5cm,侧棱长为8cm,一只蚂蚁欲从正四棱柱的底面上的点A沿棱柱侧面到点C1处吃食物,那么它需要爬行的最短路径是多少？
将四棱柱的侧面展开,连结AC1,
直角三角形两直角边分别为5厘米、12厘米，那么斜边上的高是多少？
如图，在△ABC中，∠ACB = 90。，CD是高，若AB=13cm，AC = 5cm，求CD的长；
∴AC2+BC2=AB2
18.1　勾股定理逆定理
如果直角三角形两直角边分别为a、b，斜边为c，那么
互逆命题: 两个命题中, 如果第一个命题的题设是第二个命题的结论, 而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题. 如果把其中一个叫做原命题, 那么另一个叫做它的逆命题.
互逆定理: 如果一个定理的逆命题经过证明是真命题, 那么它也是一个定理, 这两个定理叫做互逆定理, 其中一个叫做另一个的逆定理.
我们已经学习过哪些互逆的定理。
（1）任何一个命题都有逆命题；原命题与逆命题的关系是题设和结论相互转换（2）原命题正确，逆命题不一定正确；原命题不正确，逆命题可能正确。（3）一个定理未必有逆定理。
（1）等腰三角形的两底角相等
原命题：如果一个三角形是等腰三角形，那么这个三角形的两底角相等。
逆命题：如果一个三角形的两底角相等，那么这个三角形是等腰三角形。
写出下列命题的逆命题并判断它们是否成立:
（2）两直线平行，同位角相等
原命题：如果两条直线平行，那么同位角相等。
逆命题：如果同位角相等，那么两直线平行。
（3）三内角之比为1:2:3的三角形为 直角三角形
原命题：如果一个三角形三内角之比为1：2：3， 那么这个三角形是直角三角形。
逆命题：如果一个三角形是直角三角形， 那么这个三角形三内角之比为1：2：3。
说出下列命题的逆命题，并说明这些命题的逆命题成立吗？（1）两条直线平行，内错角相等；（2）如果两个实数相等，那么它们的绝对值相等；（3）全等三角形的对应角相等；（4）到角的两边距离相等的点在角的平分线上。
例1 判断由a、b、c组成的三角形是不是直角三角形：(1) a＝15 , b ＝8 , c＝17
(2) a＝13 , b ＝15 , c＝14
解：∵152＋82＝225＋64＝289 172＝289 ∴ 152＋82＝172 ∴这个三角形是直角三角形
下面以a,b,c为边长的三角形是不是直角三角形？如果是那么哪一个角是直角？
(1) a=25 b=20 c=15 ____ _____ ;
(2) a=13 b=14 c=15 ____ _____ ;
(4) a:b: c=3:4:5 _____ _____ ;
像25,20,15,能够成为直角三角形三条边长的三个正整数，称为勾股数.
A、锐角三角形 B、直角三角形C、钝角三角形 D、等边三角形
已知：如图，四边形ABCD中，∠B＝900，AB＝3，BC＝4，CD＝12，AD＝13,求四边形ABCD的面积?
分析：先来判断a,b,c三边哪条最长，可以代m,n为满足条件的特殊值来试，m=5,n=4.则a=9,b=40,c=41,c最大。
∴△ABC是直角三角形
2、什么叫做互逆命题、原命题与逆命题
3、什么称为互为逆定理。
1、运用勾股定理计算①知两边长直接求一边。②只知一边长，可运用方程求另两边。③对于含45度和30度的直角三角形，可用比例求边长。 2、运用勾股定理证明：构造直角三角形
（1）直角三角形的两条直角边长分别为3、4，则斜边长为 .（2）等腰直角三角形的腰长是1，则底边长为 . （3）直角三角形中，30度的角所对的边为5，则另两边长为 .
4、等腰三角形底边上的高为8，周长为32，求：这个三角形的面积。
5、在平面直角坐标系中，点（-3，-4）与原点之间的距离是_______，点（3，- 4）与点（2，1）之间的距离是_______.
7.若正方形的面积为3cm2，则它的对角线长是 .8.一个直角三角形的三边为三个连续偶数，则它的三边长分别为 .
6.在 ABC中,C=90°, (1)若c=10,a:b=3:4,a=____,b=___. (2)若a=8,b=15,则c=______.
9、已知，如图，在Rt△ABC中，∠C=90°，∠1=∠2，CD=1.5, BD=2.5, 求AC的长.
10、如图，一块直角三角形的纸片，两直角边AC=6㎝，BC=8㎝。现将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合，求CD的长．
11、如图，在Rt △ABC中， ∠C=90°, ∠A=15°,BC=1,求△ABC的面积。
12、 △ABC中， ∠A=45°， ∠B=30°，BC=8，求AC的边长。
13、如图，小颍同学折叠一个直角三角形的纸片，使A与B重合，折痕为DE，若已知AC=10cm，BC=6cm,你能求出CE的长吗？
14、 如图，∠ACB=∠ABD=90°，CA=CB，∠DAB=30°，AD=8，求：AC的长。
15、如图，在四边形ABCD中，∠BAD =900，∠DBC = 900 ， AD = 3，AB = 4，BC = 12， 求CD；
16、直角三角形两直角边分别为5厘米、12厘米，那么斜边上的高是多少？
8.△ABC中,周长是24,∠C=90°,且 b=6,则三角形的面积是多少?
∵周长是24，且b=6
∴a+c=24-6=18
设a=x,则c=18-x
∴x2+62=(18-x)2
已知三角形ABC中，AB=10，BC=21，AC=17，求BC边上的高线AD。
解：设BD=X，则DC=21－X。
∴AD2=AB2-BD2=102-X2
AD2=AC2-CD2=172-（21-X）2
∴102-X2=172-（21-X）2
∴AD2=102-62=64
8.△ABC中,周长是 , ∠C=90°,且 c=2,则三角形的面积是多少?
9.直角三角形中,斜边长是 , 面积为2,则三角形的周长是多少?
如图，在Rt△ABC中C=90，AC=BC,且BC=5, 求三角形ABC的面积和底边上的高
如图，在Rt△ABC中C=90， A=30，,且AC=3, 求BC的长和三角形ABC的面积
12.如图，△ABC中，∠A=45°， ∠B=30°，BC=8. 求AC的长.
6.如图,四边形ABCD中,∠B=∠D=90°,∠C=45°,AD=1,BC=2,求CD的长.
（1） ∠B=90°, ∠C=45°, BC=2
（2） ∠B=90°, ∠C=45°, 则∠E=45°
∵∠ADE=90°, ∠C=45°, AD=1
10.如图，在四边形ABCD中，∠BAD =900，∠DBC = 900 ， AD = 3，AB = 4，BC = 12，求CD和四边形ABCD的面积；
9.在等腰△ABC中，AB＝AC＝13cm ，BC=10cm,求△ABC的面积。
∵ AB＝AC, AD⊥BC
2、等腰三角形底边上的高为8，周长为32，求这个三角形的面积
解：设这个三角形为ABC，高为AD，设BD为X，则AB为（16-X），
由勾股定理得：X2+82=(16-X)2
即X2+64=256-32X+X2
∴ S∆ABC=BC•AD/2=2 •6 •8/2=48
2.三角形ABC中,AB=10,AC=17,BC边上的高线AD=8,求（1）BD （2）CD （3）BC
例4、在下图中，BC长为3厘米，AB长为4厘米，AF长为12厘米，求正方形CDEF的面积。
AC2=32+42=52
SCDEF=FC2=AF2+AC2=122+52 =132=169厘米2
例5、如图，直角三角形三边上的半圆面积之间有什么关系？
即：两直角边上的半圆面积之和等于斜边上半圆的面积。
1、小明从家出发向正北方向走了150米，接着向正东方向走到离家250米远的地方，小明向正东方向走了多远？
2、一架云梯长25米，斜靠在一面墙上，梯子底端离墙7米。（1）这个梯子的顶端距地面有多高？（2）如果梯子的顶端下滑了4米，那么梯子的底部在水平方向也滑动了4米吗？
郑凯想知道学校旗杆的高，他发现旗杆顶端的绳子垂到地面还多1米，当他把绳子的下端拉开5米后，发现下端刚好接触地面，你能帮他算出旗杆的高吗？
如图是一个三级台阶，它的每一级的长宽和高分别为20dm、3dm、2dm，A和B是这个台阶两个相对的端点，A点有一只蚂蚁，想到B点去吃可口的食物，则蚂蚁沿着台阶面爬到B点最短路程是多少？
已知：在Rt△ABC中，∠C=900, ∠A,∠B,∠C的对边分别为a,b,c,设△ABC的面积为S,周长为P
（2）如果a+b-c=m，观察上表猜想
=_______(用含有m的代数式表示)。
（3）证明（2）中的结论。
如图，长方体的长为15 cm，宽为 10 cm，高为20 cm，点B离点C 5 cm,一只蚂蚁如果要沿着长方体的表面从点 A爬到点B，需要爬行的最短距离是多少？
葭生池中 今有方池一丈， 葭生其中央， 出水一尺， 引葭赴岸， 适与岸齐。 问：水深、葭长各几何？
则有: (x-1)2+52=x2
所以：葭长13尺，水深12尺。
7.有一个圆柱,它的高等于12厘米,底面半径等于3厘米,在圆柱下底面上的A点有一只蚂蚁,它想从点A爬到点B , 蚂蚁沿着圆柱侧面爬行的最短路程是多少? (π的值取3)
长18cm (π的值取3)
∵ AB2=92+122=81+144=225=
∴ AB=15(cm)
蚂蚁爬行的最短路程是15厘米.