





人教版八年级下册17.1 勾股定理一等奖课件ppt
展开古希腊著名哲学家、数学家、 天文学家
商高是公元前十一世纪的中国人。当时中国的朝代是西周,是奴隶社会时期。在中国古代大约是战国时期西汉的数学著作《周髀算经》中记录着商高同周公的一段对话。商高说:"…故折矩,勾广三,股修四,经隅五。"什么是"勾、股"呢?在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。商高那段话的意思就是说:当直角三角形的两条直角边分别为3(短边)和4(长边)时,径隅(就是弦)则为5。以后人们就简单地把这个事实说成"勾三股四弦五"。由于勾股定理的内容最早见于商高的话中,所以人们就把这个定理叫作"商高定理"。
希腊的著明数学家毕达格拉斯有次应邀参加一位富有政要的餐会,这位主人豪华宫殿般的餐厅铺着是正方形美丽的大理石地砖,由于大餐迟迟不上桌,这些饥肠辘辘的贵宾颇有怨言;但这位善于观察和理解的数学家却凝视脚下这些排列规则、美丽的方形磁砖,但毕达哥拉斯不只是欣赏磁砖的美丽,而是想到它们[和数]之间的关系,于是 拿了画笔并且蹲在地板上,选了一块磁砖以它的对角线 AB为边画一个正方形,他发现这个正方形面积恰好等于两块磁砖的面积和。他很好奇 于是再以两块磁砖拼成的矩形之对角线作另一个正方形,他发现这个正方形之面积等于5块磁砖的面积,也就是以两股为边作正方形面积之和。至此毕达哥拉斯作了大胆的假设: 任何直角三角形,其斜边的平方恰好等于另两边平方之和。那一顿饭,这位古希腊数学大师,视线都一直没有离开地面。
希腊的著明数学家毕达格拉斯发现了这个定理,因此世界上许多国家都称勾股定理为“毕达格拉斯”定理.为了庆祝这一定理的发现,毕达哥拉斯学派杀了一百头牛酬谢供奉神灵,因此这个定理又有人叫做“百牛定理”.
一个周末的傍晚,伽菲尔德突然发现附近的一个小石凳上,有两个小孩正在聚精会神地谈论着什么,只见一个小男孩正俯着身子用树枝在地上画着一个直角三角形.于是伽菲尔德便问他们在干什么?只见那个小男孩头也不抬地说:“ 请问先生,如果直角三角形的两条直角边分别为 3和4,那么斜边长为多少呢?”伽菲尔德答到:“是5呀.”小男孩又问道:“如果两条直角边分别为5和7,那么这个直角三角形的斜边长又是多少?”伽菲尔德不加思索地回答到:“那斜边的平方一定等于5的平方加上7的平方.”小男孩又说道:“先生,你能说出其中的道理吗?”伽菲尔德一时语塞,无法解释了,心理很不是滋味. 于是伽菲尔德不再散步,立即回家,潜心探讨小男孩给他留下的难题.他经过反复的思考与演算,终于弄清楚了其中的道理,并给出了简洁的证明方法.1881年,伽菲尔德就任美国第二十任总统后来,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就把这一证法称为“总统”证法。
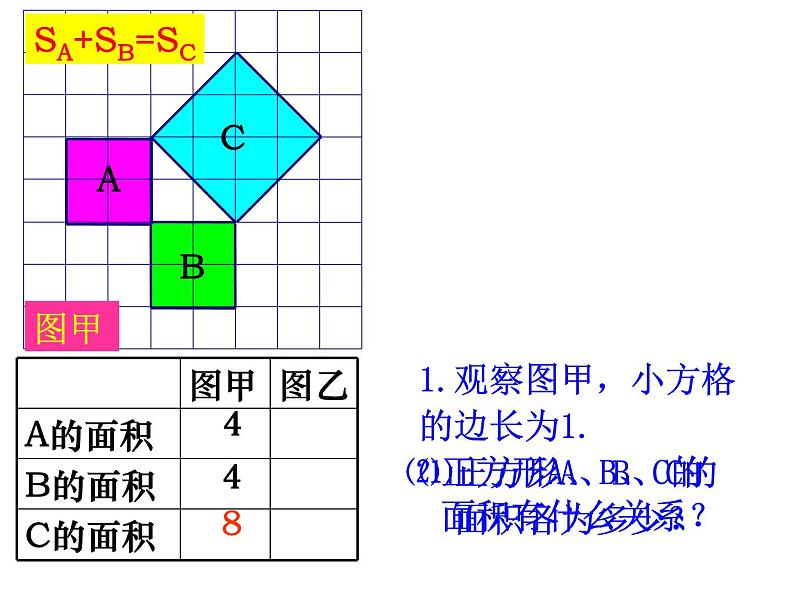
1.观察图甲,小方格的边长为1.⑴正方形A、B、C的 面积各为多少?
⑵正方形A、B、C的 面积有什么关系?
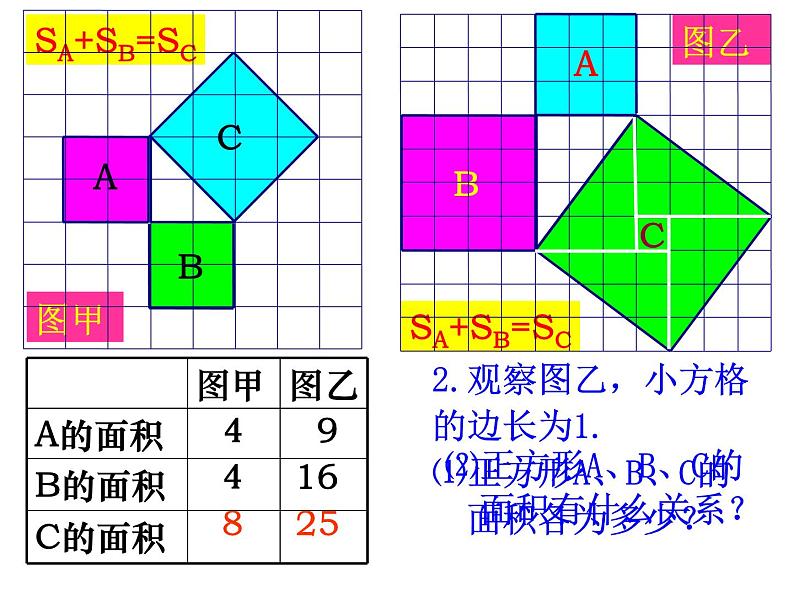
2.观察图乙,小方格的边长为1.⑴正方形A、B、C的 面积各为多少?
2.观察图乙,小方格的边长为1.
3.猜想a、b、c 之间的关系?
如果直角三角形两直角边分别为a, b,斜边为c,那么
即直角三角形两直角边的平方和等于 斜边的平方.
是不是所有的直角三角形都具有这样的特点呢?这就需要我们对一个一般的直角三角形进行证明.到目前为止,对这个命题的证明方法已有几百种之多.下面我们就来看一看我国数学家赵爽是怎样证明这个命题的.
看左边的图案,这个图案是公元 3 世纪我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.赵爽根据此图指出:四个全等的直角三角形(红色)可以如图围成一个大正方形,中间的部分是一个小正方形 (黄色).
化简得: c2 =a2+ b2.
这个图形里蕴涵着怎样博大精深的知识呢?
它标志着我国古代数学的伟大成就!
勾股定理(毕达哥拉斯定理) (gu-gu therem)
如果直角三角形两直角边分别为a, b,斜边为c,那么
1、如图:Rt△ABC中,∠C=90°,AC=12,BC=5,求AB的长解:在Rt△ABC中,∠C=____°,BC=____ , AC=____ ,根据勾股定理得 AB²= ²+ ²所以 AB= =
2、如图:Rt△ABC中,∠C=90°,AB=10,BC=6,求AC的长解:在Rt△ABC中,∠C=____°,BC=____ , AB=____ ,根据勾股定理得 AC²= ²- ²所以 AC= = ______
求下列直角三角形中未知边的长:
可用勾股定理建立方程.
1、Rt△ABC中,∠B=90°,AC=160, BC=128,求AB的长 (要求:画出示意图,并写出求解过程)
2、在波平如静的湖面上,有一朵美丽的红莲 ,它高出水面1米 ,一阵大风吹过,红莲被吹至一边,花朵齐及水面,如果知道红莲移动的水平距离为2米 ,问这里水深多少?
x2+22=(x+1)2
勾股定理从边的角度刻画了直角三角形的又一个特征. 人类对勾股定理的研究已有近3000年的历史,在西方,勾股定理又被称为“毕达哥拉斯定理”、“百牛定理”、“驴桥定理”等等 .
收集有关勾股定理的证明方法,下节课展示、交流.
数学八年级下册17.2 勾股定理的逆定理优秀课件ppt: 这是一份数学八年级下册17.2 勾股定理的逆定理优秀课件ppt,共13页。PPT课件主要包含了你知道吗,画一画,明确下面问题等内容,欢迎下载使用。
初中人教版17.1 勾股定理一等奖ppt课件: 这是一份初中人教版17.1 勾股定理一等奖ppt课件,共36页。PPT课件主要包含了SA+SBSC,a2+b2c2,用拼图法证明,证法一,S大正方形=c2,证法二,美国总统的证明,证法三等内容,欢迎下载使用。
八年级下册17.1 勾股定理获奖课件ppt: 这是一份八年级下册17.1 勾股定理获奖课件ppt,共30页。PPT课件主要包含了勾股定理1,看一看,单位面积,SA+SBSC,议一议,Sa+SbSc,a2+b2c2,勾股定理,毕达哥拉斯定理,拼一拼试一试等内容,欢迎下载使用。













