初中数学29.2 三视图精品ppt课件

第二十九章  投影与视图

29.2  三视图

第3课时  由三视图确定几何体的面积或体积

学习目标：

1.   能熟练地画出物体的三视图和由三视图想象出物体形状，进一步提高空间想象能力.
2.   由三视图想象出立体图形后能进行简单的面积或体积的计算.

重点：由三视图想象出立体图形后能进行简单的面积或体积的计算.

难点：能熟练地画出物体的三视图和由三视图想象出物体形状，进一步提高空间想象能力.

一、知识链接

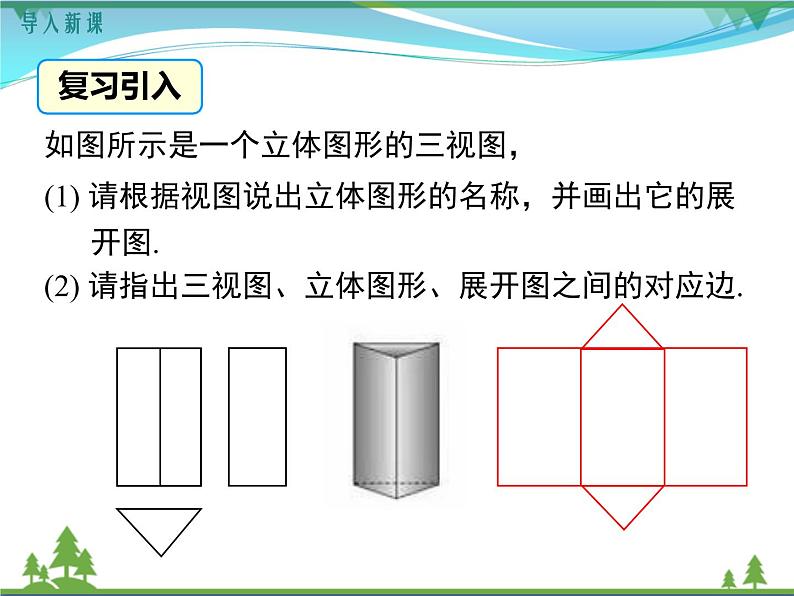
如图所示是一个立体图形的三视图，

(1) 请根据视图说出立体图形的名称，并画出它的展开图.

(2) 请指出三视图、立体图形、展开图之间的对应边.

一、要点探究

探究点1：三视图的有关计算

【典例精析】

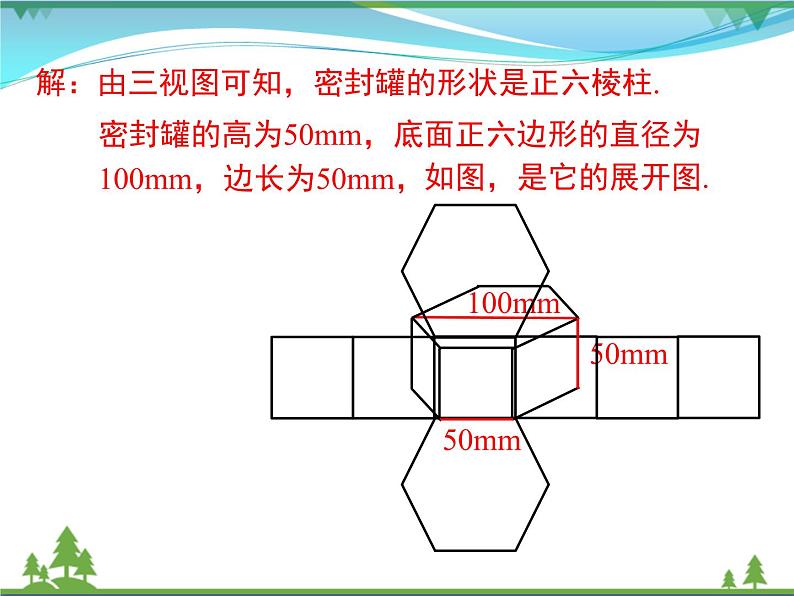
例1   某工厂要加工一批密封罐，设计者给出了密封罐的三视图，请你按照三视图确定制作每个密封罐所需钢板的面积 (图中尺寸单位：mm).

分析：1. 应先由三视图想象出密封罐的立体形状；2. 画出物体的展开图.

【归纳总结】    1. 三种图形的转化：

三视图      立体图      展开图

2. 由三视图求立体图形的面积的方法：

    (1) 先根据给出的三视图确定立体图形，并确定立体图形的长、宽、高.

    (2) 将立体图形展开成一个平面图形 (展开图)，观察它的组成部分.

    (3) 最后根据已知数据，求出展开图的面积.

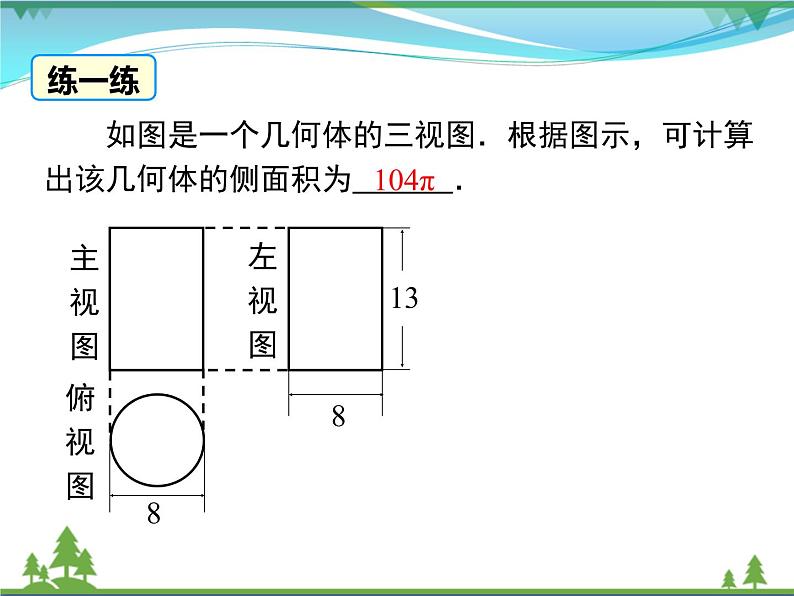
练一练 如图是一个几何体的三视图．根据图示，可计算出该几何体的侧面积为         ．

【典例精析】

例2 如图是一个几何体的三视图，根据所示数据，求该几何体的表面积和体积.

分析：由三视图可知该几何体是由圆柱、长方体组合而成.  分别计算它们的表面积和体积，然后相加即可.

练一练  一个机器零件的三视图如图所示(单位：cm)，这个机器零件是一个什么样的立体图形？它的体积是多少？

二、课堂小结

1. 三种图形的转化：

三视图      立体图       展开图

2. 由三视图求立体图形的面积的方法：

(1) 先根据给出的三视图确定立体图形，并确定立体图形的长、宽、高.

(2) 将立体图形展开成一个平面图形 (展开图)，观察它的组成部分.

(3) 最后根据已知数据，求出展开图的面积.

1. 一个长方体的左视图、俯视图及相关数据如图所示，则其主视图的面积为   (    ) 

  A. 6            B. 8         C. 12           D. 24

2. 如图是一个几何体的三视图，根据图中提供的数据(单位：cm)，可求得这个几何体的体积为          .

3. 如图是某几何体的三视图及相关数据(单位：cm)，则该几何体的侧面积为          cm2.

4. 如图是一个由若干个棱长为1cm的正方体构成的几何体的三视图．

  (1) 请写出构成这个几何体的正方体的个数为            ；

  (2) 计算这个几何体的表面积为           ．

5.如图是一个几何体的三视图，试描绘出这个零件的形状，并求出此三视图所描述的几何体的表面积.

6.某一空间图形的三视图如图所示，其中主视图是半径为1的半圆以及高为 1 的矩形；左视图是半径为1 的四分之一圆以及高为1的矩形；俯视图是半径为1 的圆，求此图形的体积 (参考公式：V球＝πR3)．

参考答案

自主学习

一、知识链接

（1）三棱柱 

(2)略

合作探究

一、要点探究

探究点1：三视图的有关计算

【典例精析】

例1 解：由三视图可知，密封罐的形状是正六棱柱.密封罐的高为50mm，底面正六边形的直径为100mm，边长为50mm，如图，是它的展开图.

由展开图可知，制作一个密封罐所需钢板的面积为

练一练  104π

【典例精析】

例2  解：该图形上、下部分分别是圆柱、长方体，根据图中数据得：表面积为20×32π+30×40×2+25×40×2+25×30×2=(5 900+640π)(cm2),体积为25×30×40+10²×32π=

(30 000+3 200π)(cm3).

练一练 解：长方体，其体积为10×12×15=1800(cm3).

当堂检测

1.   B  2.  3 cm3    3.  2π    4.（1）5   （2）20cm2

5.解：该几何体的表面积为π×2²+2π×2×2+×4×4π=20 π.

6.解：由已知可得该几何体是一个下部为圆柱，上部为球的组合体．由三视图可得，下部圆柱的底面半径为1，高为1，则V圆柱＝π，上部球的半径为1，则＝，故此几何体的体积为.