人教版九年级下册第二十九章 投影与视图29.2 三视图精品第3课时同步训练题

29.2 三视图（第3课时）

自主预习

1．一个几何体的三视图如图所示，其中主视图和左视图都是腰长为4、底边为2的等腰三角形，则这个几何体的侧面展开图的面积为(　　)

A．2π        B. π         C．4π          D．8π

1题图                                 2题图

2．如图是由一些大小相同的小立方体组成的几何体的主视图和左视图，则组成这个几何体的小立方体的个数不可能是(　　)

A．3个     B．4个       C．5个       D．6个

3．如图是一个由若干个棱长相等的正方体构成的几何体的三视图．

(1)请写出构成这个几何体的正方体个数；

(2)请根据图中所标的尺寸，计算这个几何体的表面积．

                                                       3题图

互动训练

知识点一：几何体的展开图

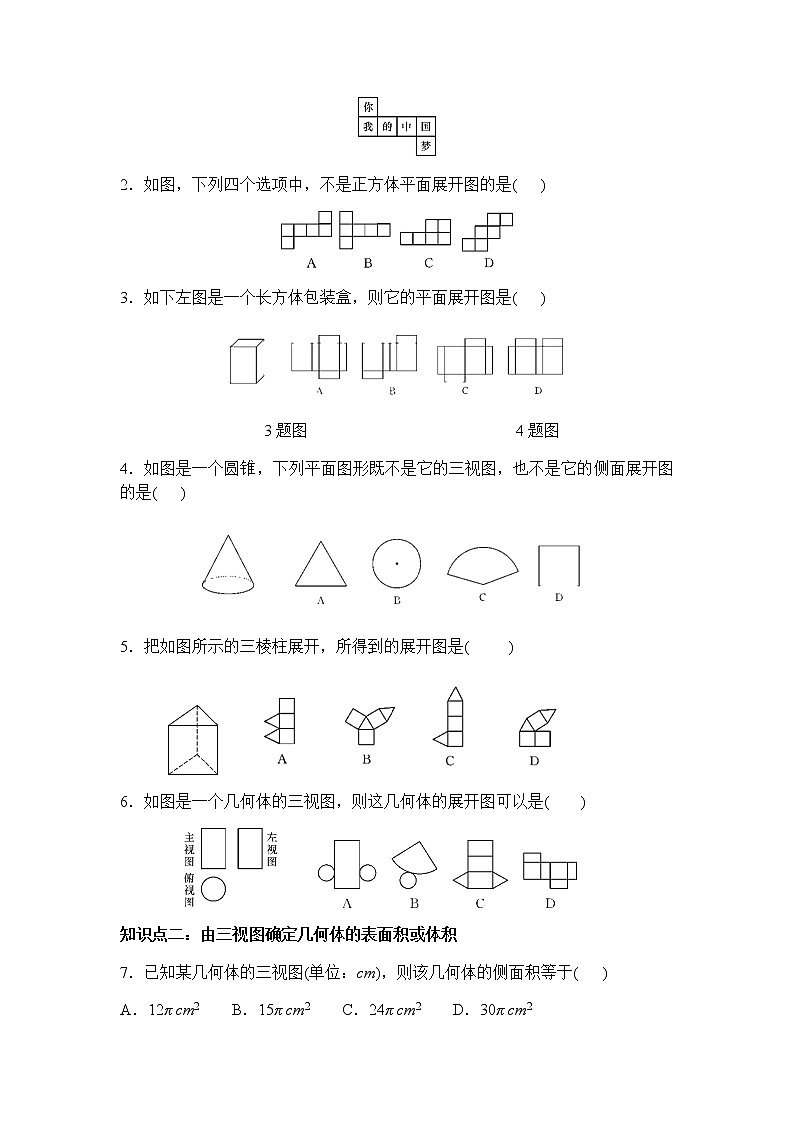
1．如图是一个正方体展开图，把展开图折叠成正方体后，“你”字一面相对面上的字是(    )

  A．我        B．中       C．国       D．梦

2．如图，下列四个选项中，不是正方体平面展开图的是(   )

3．如下左图是一个长方体包装盒，则它的平面展开图是(   )

                  3题图                          4题图 

4．如图是一个圆锥，下列平面图形既不是它的三视图，也不是它的侧面展开图的是(   )

5．把如图所示的三棱柱展开，所得到的展开图是(     )

6．如图是一个几何体的三视图，则这几何体的展开图可以是(    )

知识点二：由三视图确定几何体的表面积或体积

7．已知某几何体的三视图(单位：cm)，则该几何体的侧面积等于(   )

A．12π cm2    B．15π cm2    C．24π cm2    D．30π cm2

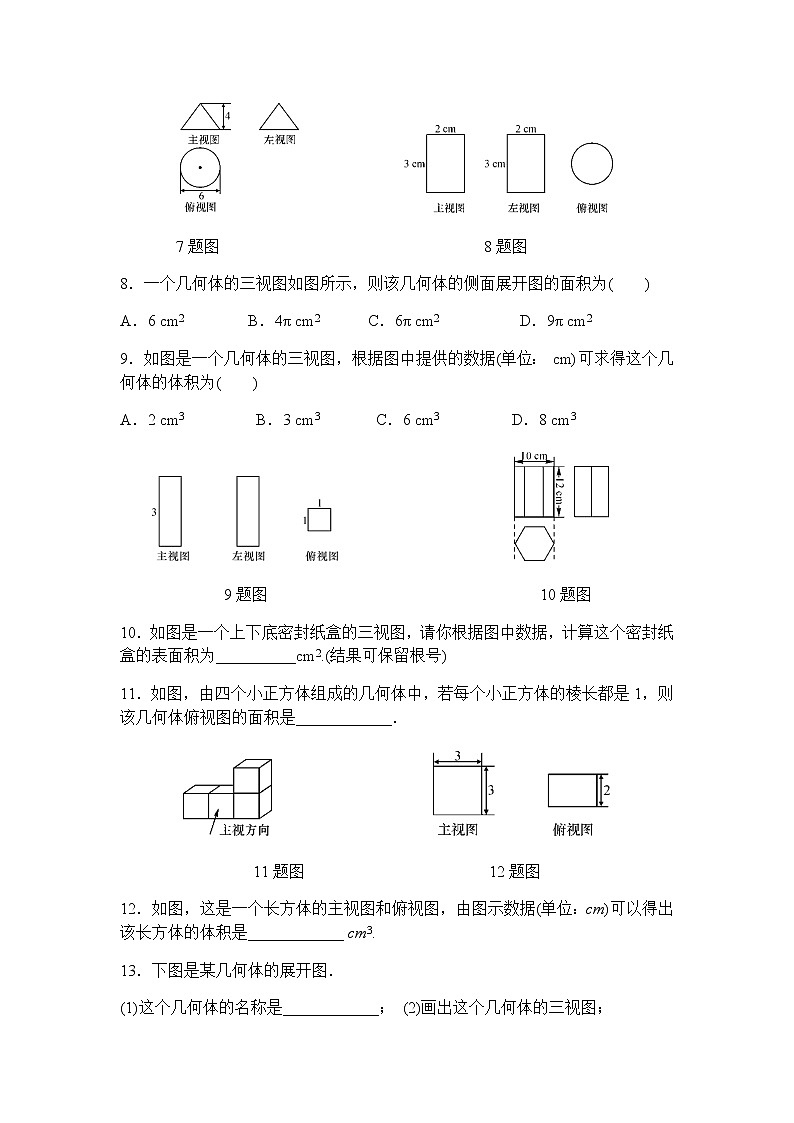
       7题图                                 8题图

8．一个几何体的三视图如图所示，则该几何体的侧面展开图的面积为(　　)

A．6 cm2        B．4π cm2      C．6π cm2          D．9π cm2

9．如图是一个几何体的三视图，根据图中提供的数据(单位： cm)可求得这个几何体的体积为(　　)

A．2 cm3         B．3 cm3       C．6 cm3         D．8 cm3

9题图                                  10题图

10．如图是一个上下底密封纸盒的三视图，请你根据图中数据，计算这个密封纸盒的表面积为__________cm2.(结果可保留根号)

11．如图，由四个小正方体组成的几何体中，若每个小正方体的棱长都是1，则该几何体俯视图的面积是____________．

11题图                       12题图  

12．如图，这是一个长方体的主视图和俯视图，由图示数据(单位：cm)可以得出该长方体的体积是____________ cm3.

13．下图是某几何体的展开图．

(1)这个几何体的名称是____________； (2)画出这个几何体的三视图；

(3)求这个几何体的体积．(π取3.14)

14. 某个几何体的三视图如图所示，根据图中有关数据，求这个几何体的各个侧面积之和.

课时达标

1.一个长方体的三视图如图，若其俯视图为正方形，则这个长方体的体积为(   )

A.66       B.36       C.48       D.48+36

      1题图                             2题图

2.如图是一个几何体的三视图(图中尺寸单位：cm).根据图中所示数据求得这个几何体的侧面积是(    )

A.12cm2       B. (12＋π) cm2       C. 6πcm2         D. 8πcm2

3. 如图是某几何体的三视图及相关数据，则该几何体的侧面积是（　　）

  A. ac         B. bc        C. ac      D. bc

4．一个圆柱的侧面展开图是两邻边长分别为6和8的矩形，则该圆柱的底面圆半径是(    )

   A.           B.           C.或            D.或

5．如图是一个正六棱柱的主视图和左视图，则图中的a＝(　　)

A．2         B.        C．2        D．1

5题图                           6题图

6．如图是某几何体的三视图，根据图中数据，求得该几何体的体积为(   )

   A．60π      B．70π      C．90π     D．160π

7．图1是一个小正方体的表面展开图，小正方体从图2所示的位置依次翻到第1格、第2格、第3格、第4格，这时小正方体朝上一面的字是(     )

  A．梦        B．水         C．城         D．美

8．如图，在一次数学活动课上，张明用17个边长为1的小正方体搭成了一个几何体，然后他请王亮用其他同样的小正方体在旁边再搭一个几何体，使王亮所搭几何体恰好可以和张明所搭的几何体拼成一个大长方体(不改变张明所搭几何体的形状)，那么王亮至少还需要____________个小正方体，王亮所搭几何体表面积为____________．

     8题图                    9题图                      10题图

9．从棱长为2的正方体毛坯的一角，挖去一个棱长为1的小正方体，得到一个如图所示的零件，则这个零件的表面积为____________．

10．如图是一个上下底密封纸盒的三视图，请你根据图中数据，计算这个密封纸盒的表面积为____________cm2.(结果可保留根号)

11．如图是某工件的三视图，求此工件的全面积．

11题图

12．如图是一个几何体的三视图(单位：厘米)．

(1)写出这个几何体的名称；

(2)根据所示数据计算这个几何体的表面积；

(3)如果一只蚂蚁要从这个几何体中的点B出发，沿表面爬到AC的中点D，请你求出这个线路的最短路程．

拓展探究

1．如图是一个几何体的三视图(单位：厘米)．

(1)写出这个几何体的名称；

(2)根据所示数据计算这个几何体的表面积；

(3)如果一只蚂蚁要从这个几何体中的点B出发，沿表面爬到AC的中点D，请你求出这个线路的最短路程．

2.如图是一个几何体的主视图和俯视图,试求该几何体的体积(取3.14).

29.2 三视图（第3课时）答案

自主预习

1. C.  2. D. 

3．解：(1)5个．(2)S表＝5×6a2－2×5a2＝20a2.

互动训练

1．D. 　2. C. 　3. A. 　4. D. 　5. B. 　6. A. 　7. B.  8. C.  9. B.

10. 75＋360　 11. 3.   12. 18. 

13．(1)圆柱

(2)三视图为：

(3)体积为：πr2h＝3.14×52×20＝1 570.

14. 解：由三视图可知，这个几何体是三棱柱，

∵底面是直角三角形，一直角边是4，斜边长是6，

∴另一直角边长是=2，

∴三棱柱的侧面积之和为：(4+6+2)×10=100+20.

故答案为：100+20.

课时达标

1. B. 解析：根据主视图，可得底面正方形的边长为3，长方体的高为4，所以这个长方体的体积V=3×3×4=36.故选B.

2. C. 解析：由三视图知该几何体是圆柱体，且底面直径是2cm，高是3cm，则其侧面积为2π×3=6π(cm2).

3. D. 解析：由题意得底面直径为c，母线长为b，

∴几何体的侧面积为．

4. C.  5. B.  6.B　7.A　

8.19，48　  9.24　10. (75＋360)

11．解：由三视图可知，该工件为底面半径为10 cm，高为30 cm的圆锥体．

这圆锥的母线长为＝10(cm)，

圆锥的侧面积为×20π×10＝100π(cm2)，

圆锥的底面积为102π＝100π(cm2)，

圆锥的全面积为100π＋100π＝100(1＋)π(cm2)．

11题图

12．解：(1)圆锥．

(2)表面积S＝S扇形＋S圆＝πrl＋πr2＝12π＋4π＝16π(平方厘米)．

(3)如图将圆锥侧面展开，线段BD为所求的最短路程．

由条件得，∠BAB′＝120°，C为弧BB′的中点，

∴BD＝3(厘米)．

拓展探究

1.(1)圆锥．

(2)表面积S＝S扇形＋S圆＝πrl＋πr2＝12π＋4π＝16π(平方厘米)．

(3)

如图将圆锥侧面展开，线段BD为所求的最短路程．由条件得，∠BAB′＝120°，C为弧BB′的中点，∴BD＝3(厘米)．

2. 解:由几何体的主视图和俯视图可知,

几何体下面部分是一个长为30cm,高40cm,宽25cm的长方体

上面部分是一个底面直径为20cm,高为32cm的圆柱

∴该几何体的体积为：30×40×5+×32 ≈ 40048. 

答:这个几何体的体积为40048cm3.