初中数学北师大版八年级上册5 应用二元一次方程组——里程碑上的数评课课件ppt

这是一份初中数学北师大版八年级上册5 应用二元一次方程组——里程碑上的数评课课件ppt，共24页。PPT课件主要包含了学习目标，题目大意，想一想，古题今解二，小试牛刀2，达标检测，回顾反思，延伸迁移，结束语，鸡兔同笼等内容，欢迎下载使用。
1、通过小组合作，分析“鸡兔同笼”等简单问题中的数量关系，学生能准确找出等量关系。2、通过列二元一次方程组解决实际问题的过程，总结用方程组解决实际问题的一般步骤，体会方程（组）是刻画现实世界的有效模型，发展模型思想和应用意识。3、通过交流，体会我国古代数学的光辉成就，体验古代数学的趣味性，激发学生对数学的好奇心和求知欲。
《孙子算经》是我国古代一部较为普及的算书,许多问题浅显有趣,其中下卷第31题”雉兔同笼”流传尤为广泛,飘洋过海流传到了日本等国.
今有鸡兔同笼, 上有三十五头, 下有九十四足, 问鸡兔各几何?
你有哪些方法来解决它呢？
今有牛五、羊二，直金十两．牛二、羊五，直金八两．牛、羊各直金几何？
5头牛、2只羊共价值10两“金”；2头牛、5只羊共价值8两“金”.问每头牛、每只羊各价值多“金”？
设每头牛价值为x两，每只羊价值y两.
（1）审题；（2）找两个等量关系；（3）设两个未知数，（4）根据等量关系列方程，联立方程组；（5）解方程组；（6）检验（7）作答.
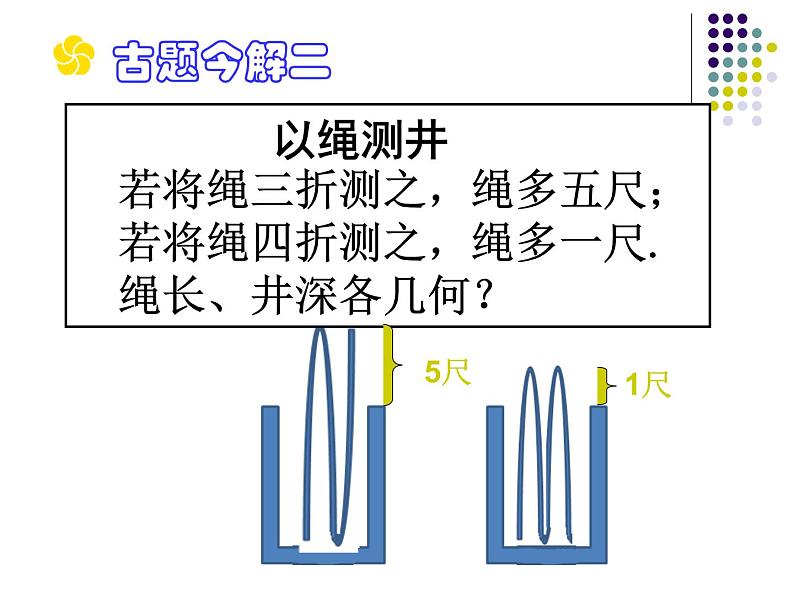
以绳测井 若将绳三折测之，绳多五尺； 若将绳四折测之，绳多一尺. 绳长、井深各几何？
隔壁听到人分银，不知人数不知银。每人五两多六两，每人六两少五两。多少人数多少银？
解：设有x个人，y两银，由题意得：
古有一捕快，一天晚上他在野外的一个茅屋里，听到外边来了一群人在吵闹，他隐隐约约地听到几个声音，下面有这一古诗为证：
每人五两多六两，每人六两少五两。
（只列方程组，不求解）
用一根绳子围绕一个大树，若环绕大树3周，则绳子还多4尺；若环绕大树4周，则绳子又少了3尺。这根绳子有多长？环绕大树一周需要多少尺？
解：设环绕大树一周需要x尺，这根绳子长y尺，由题意得：
1 用一根绳子围绕一个大树，若环绕大树3周，则绳子还多4尺；若环绕大树4周，则绳子又少了3尺。这根绳子有多长？环绕大树一周需要多少尺？
2.《算法统宗》中记载了一个问题，大意是：100个和尚分100个馒头，大和尚1人分3个馒头，小和尚3人分1个馒头。问大、小和尚个有多少人？
解：设大和尚x人，小和尚y人，由题意得：
请谈谈本节课你的收获和体会。
请根据给出的方程组 编一道实际应用题。
“一切问题都可以转化为数学问题，一切数学问题都可以转化为代数问题，而一切代数问题又都可以转化为方程问题，因此，一旦解决了方程问题，一切问题将迎刃而解!
⑴算书法：《孙子算经》中记载的算法：
47－35=12（只）
35－12=23（只）
(2)一元一次方程法 解：设鸡有x只，则兔有(35－x)只，由题意得： 2x＋4（35－x）＝94
今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何？
题中的已知量是什么？未知量？各量之间的关系呢？如果，我们用两个未知数分别表示鸡与兔的数量呢？
（1）题中有哪两个等量关系？
+ =35
+ =94
解：设鸡为x只，兔为y只，依题意得:
答：鸡有23只，兔有12只。
解:设每头牛值”金”x两,每头羊值”金”y两, 由题意,得
等量关系： （井深+5）× 3=绳长 （井深+1）× 4=绳长
所以绳长48尺，井深11尺。
解：设绳长x尺，井深y尺，则由题意得
等量关系： 井深×3+ 5×3=绳长 井深× 4+ 1×4 =绳长