数学九年级下册2.5 直线与圆的位置关系备课课件ppt

这是一份数学九年级下册2.5 直线与圆的位置关系备课课件ppt，共13页。PPT课件主要包含了知识回顾，⑴点在圆内，⑵点在圆上，⑶点在圆外，数量关系，位置关系，令OPd，知识探究，直线与圆O无公共点，公共点个数等内容，欢迎下载使用。

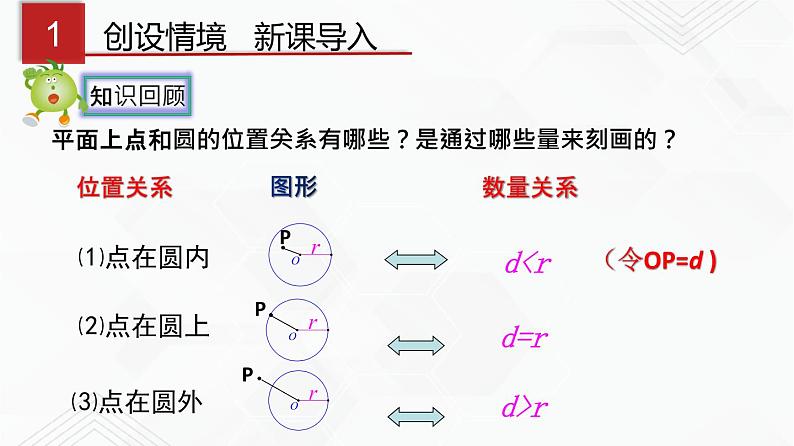
平面上点和圆的位置关系有哪些？是通过哪些量来刻画的？
1、如果我们把太阳看成一个圆，地平线看成一条直线，那你能根据直线和圆的公共点个数想象一下，直线和圆有几种位置关系吗？
三种：两个 一个 没有
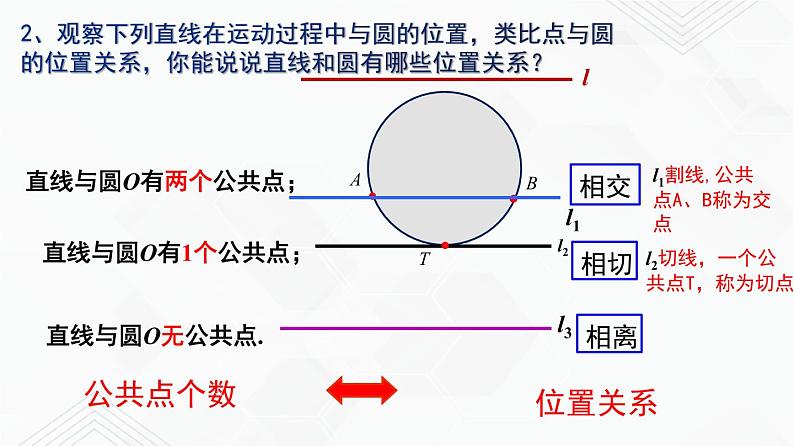
2、观察下列直线在运动过程中与圆的位置，类比点与圆的位置关系，你能说说直线和圆有哪些位置关系？
直线与圆O有两个公共点；
直线与圆O有1个公共点；
l1割线,公共点A、B称为交点
l2切线，一个公共点T，称为切点
知识点❷用数量关系判断直线与圆的位置关系
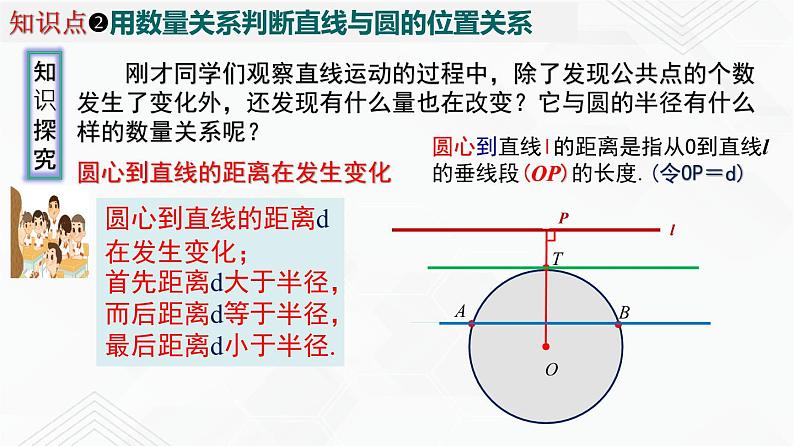
刚才同学们观察直线运动的过程中，除了发现公共点的个数发生了变化外，还发现有什么量也在改变？它与圆的半径有什么样的数量关系呢？
圆心到直线的距离在发生变化
圆心到直线l的距离是指从O到直线l的垂线段(OP)的长度.(令OP＝d)
圆心到直线的距离d在发生变化；首先距离d大于半径，而后距离d等于半径，最后距离d小于半径.
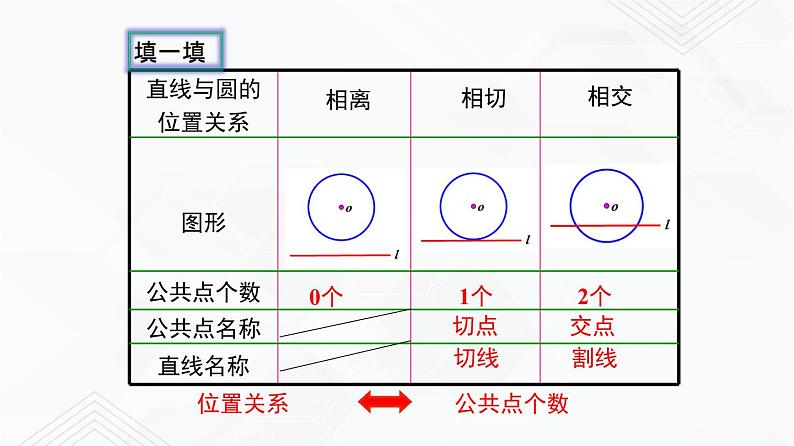
用圆心O到直线的距离d与圆的半径r的关系来区分
0cm≤d < 5cm
3.如图，∠APB=30°，圆心在PB上的⊙O的半径为1cm，OP=3cm，若⊙O沿BP方向平移，当⊙O与PA相切时，圆心O平移的距离为_____________．
例1 如图，∠C=30°，O为BC上一点，且CO=6cm，以O为圆心，r为半径的圆与直线CA有怎样的位置关系？为什么？（1）r=2.5cm；（2）r=3cm；（3）r=5cm.
解：过O点作OD⊥CA交CA于D.
在Rt△CDO中， ∠C=30°，
即圆心O到直线CA的距离d=3cm.
（1）r=2.5cm时，有d＞r，因此⊙O与直线CA相离；
（2）r=3cm时，有d=r，因此⊙O与直线CA相切；
（3）r=5cm时，有d＜r，因此⊙O与直线CA相交.
1．直线和圆相交，圆的半径为r,且圆心到直线的距离为5，则有（ ） A. r < 5 B. r > 5 C. r = 5 D. r ≥ 52. ⊙O的最大弦长为8，若圆心O到直线l的距离为d=5，则直线l与⊙O .3. ⊙O的半径为5,直线l上的一点到圆心O的距离是5，则直线l与⊙O的位置 关系是（ ）A. 相交或相切 B. 相交或相离 C. 相切或相离 D. 上三种情况都有可能
4.在Rt△ABC中，∠C=90°，AC=3cm，BC=4cm，以C为圆心，r为半径作圆，
(1)当r满足______________时，⊙C与直线AB相离.
(2)当r满足____________ 时，⊙C与直线AB相切.
(3)当r满足____________时，⊙C与直线AB相交.
5、 如图，在平面直角坐标系中，⊙A与y轴相切于原点O，平行于x轴的直线交⊙A于M、N两点．若点M的坐标是(－4，－2)，则点N的坐标为(　　)A．(－1，－2) B．(1，2) C．(－1.5，－2) D．(1.5，－2)
解析：过点A作AQ⊥MN于Q，连接AN.设半径为r，由垂径定理有MQ＝NQ，所以AQ＝2，AN＝r，NQ＝4－r.利用勾股定理可以求出NQ＝1.5，所以N点坐标为(－1，－2)．故选A.
方法总结：在圆中如果有弦要求线段的长度，通常要将经过圆心的半径画出，利用垂径定理和勾股定理解决问题．