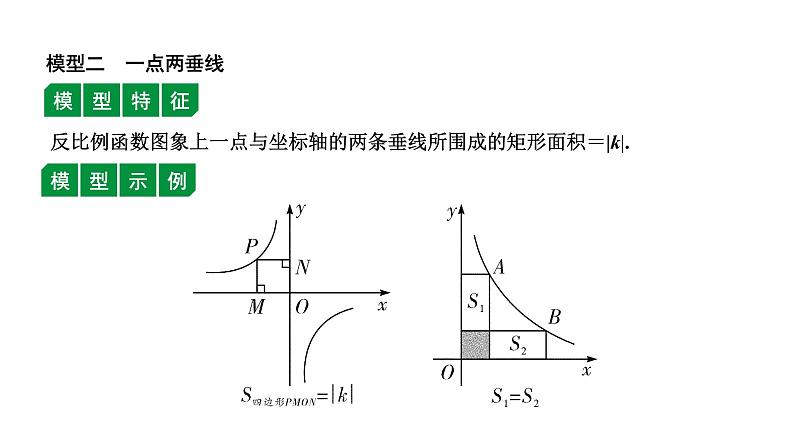
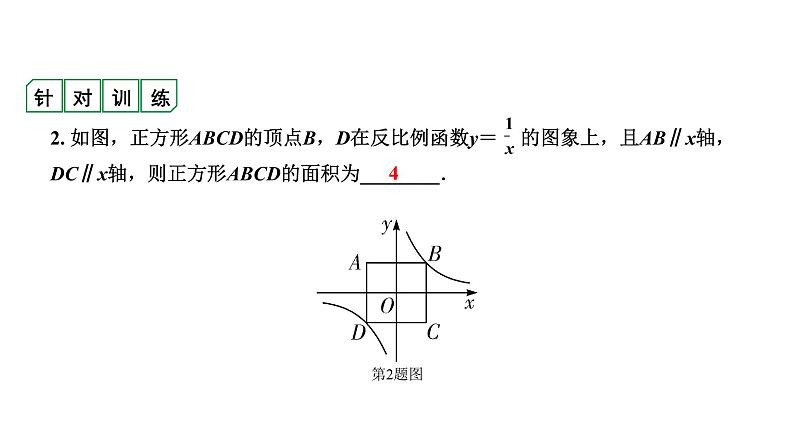
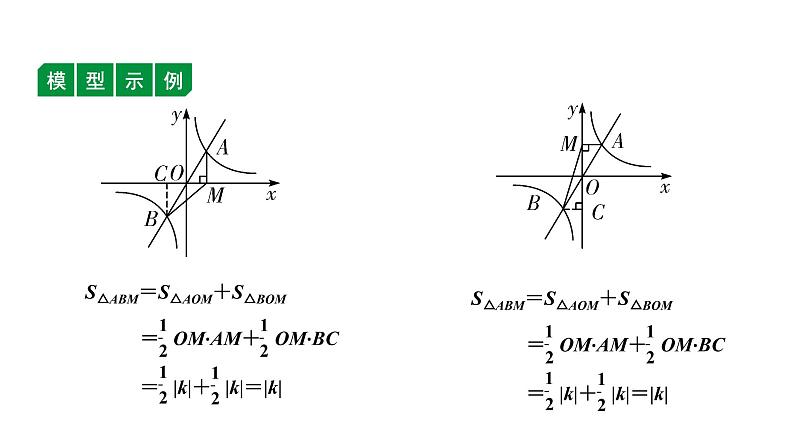
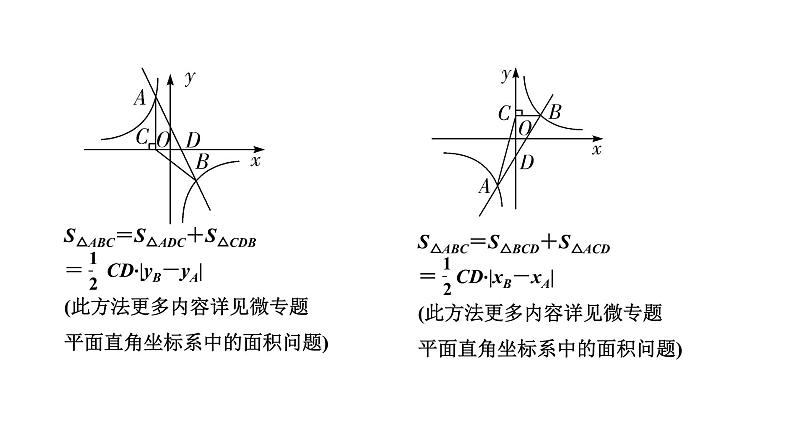
福建2020中考数学一轮培优 第三章 函数 试卷练习课件

第三章　函数

第四节  反比例函数的图象与性质（含与一次函数结合）

(建议时间：　　　　分钟)

基础过关

1. 已知反比例函数y＝(k≠0)的图象经过点(1，－3)，则此反比例函数的关系式为(　　)

A. y＝  B.  y＝ 

C.  y＝－   D.  y＝－

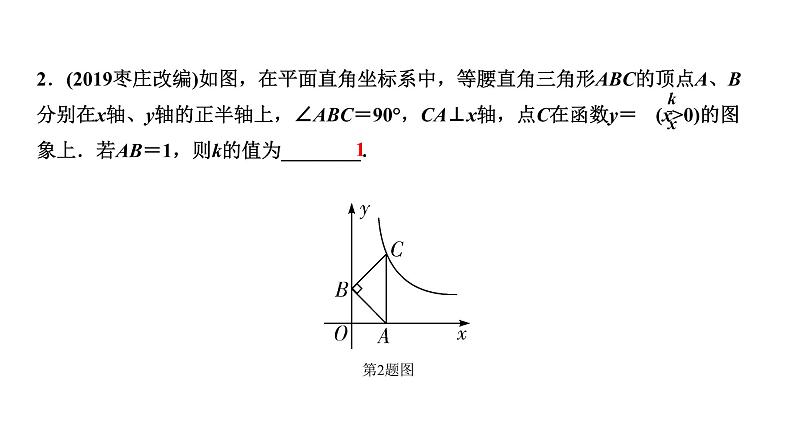
2. (2019广州) 若点A(－1，y1)，B(2，y2)，C(3，y3)在反比例函数y＝的图象上，则y1，y2，y3的大小关系是(　　)

A. y3＜y2＜y1  B. y2＜y1＜y3

C. y1＜y3＜y2  D. y1＜y2＜y3

3. (2019淮安)当矩形面积一定时，下列图象中能表示它的长y和宽x之间的函数关系的是(　　)

4. (2019江西)已知正比例函数y1的图象与反比例函数y2的图象相交于点A(2，4)，下列说法正确的是(　　)

A. 反比例函数y2的解析式是y2＝－

B. 两个函数图象的另一交点坐标为(2，－4)

C. 当x＜－2或0＜x＜2时，y1＜y2

D. 正比例函数y1与反比例函数y2都随x的增大而增大

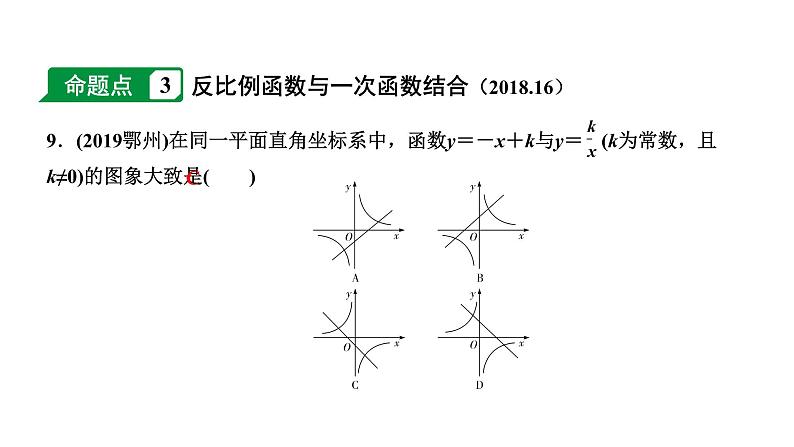
5.  (2019贺州)已知ab＜0，一次函数y＝ax－b与反比例函数y＝在同一直角坐标系中的图象可能是(　　)

6. (2019海南改编)如果反比例函数y＝(a是常数)的图象在第一、三象限，那么a的取值范围是　　　　.

7. (2019邵阳)如图，在平面直角坐标系中，点A的坐标为(－4，2)，反比例函数y＝(x＜0)的图象经过线段OA的中点B，则k＝　　　　.

第7题图

8. 已知反比例函数y＝(k≠0)的图象经过(3，－1)，则当1＜y＜3时，自变量x的取值范围是　　　　.

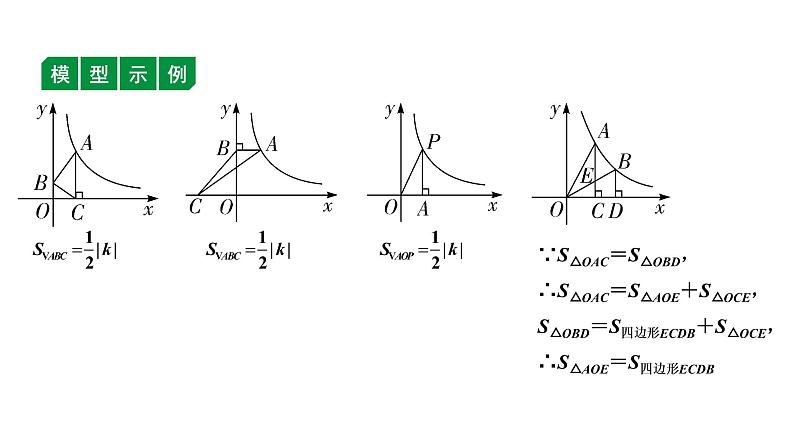
9. (2020原创)如图，点A(3，n)在双曲线y＝上，过点A作AC⊥x轴，垂足为C. 线段OA的垂直平分线交OC于点M，则△AMC周长的值是　　　　.

第9题图

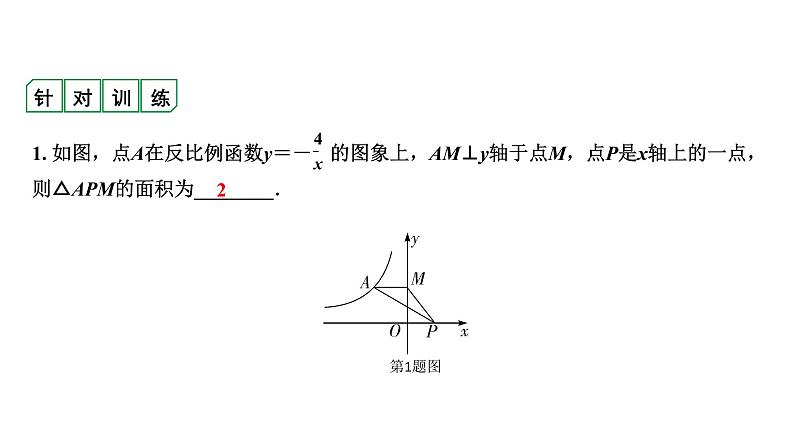
10. (2019宁德5月质检)已知反比例函数图象上两点A(2，3)，B(－2x＋2，y1)的位置如图所示.

(1)求x的取值范围；

(2)若点C(－x，y2)也在该反比例函数的图象上，试比较y1，y2的大小.

第10题图

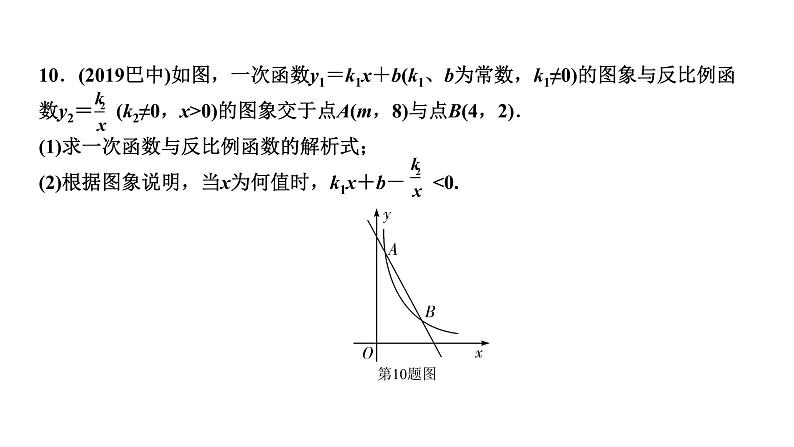
11. (2019甘肃省卷)如图，已知反比例函数y＝(k≠0)的图象与一次函数y＝－x＋b的图象在第一象限交于A(1，3)，B(3，1)两点.

(1)求反比例函数和一次函数的表达式；

(2)已知点P(a，0)(a>0)，过点P作平行于y轴的直线，在第一象限内交一次函数y＝－x＋b的图象于点M，交反比例函数y＝的图象于点N.若PM>PN，结合函数图象直接写出a的取值范围.

第11题图

12. (2019福建逆袭卷)某市准备举行夏季运动会，需要定制一批服装，预计需要9000套，某服装厂通过竞标得到这批服装的订单.

(1)求每天生产的套数y(套)与生产的时间x(天)之间的函数关系式；

(2)如果生产车间每天生产300套服装，那么多少天可以完成任务？

(3)已知运动会还有15天开始，服装必须在10天内制作完成，那么生产车间每天至少要生产多少套服装？

能力提升

1. (2018无锡)已知点P(a，m)，Q(b，n)都在反比例函数y＝－的图象上，且a＜0＜b，则下列结论一定正确的是(　　)

A.m＋n＜0  B.m＋n>0

C.m＜n  D.m>n

2. (2019益阳)反比例函数y＝的图象上有一点P(2，n)，将点P向右平移1个单位，再向下平移1个单位得到点Q，若点Q也在该函数的图象上，则k＝　　　　.

3. (2019广东省卷)如图，一次函数y＝k1x＋b的图象与反比例函数y＝的图象相交于A、B两点，其中点A的坐标为(－1，4)，点B的坐标为(4，n).

(1)根据图象，直接写出满足k1x＋b＞的x的取值范围；

(2)求这两个函数的表达式；

(3)点P在线段AB上，且S△AOP∶S△BOP＝1∶2，求点P的坐标.

第3题图

满分冲关

1. 在平面直角坐标系xOy中，对于不在坐标轴上的任意一点P(x，y)，我们把点P′(，)称为点P的“倒影点”.直线y＝－x＋1上有两点A，B，它们的倒影点A′，B′均在反比例函数y＝的图象上，若AB＝2，则k＝　　　　.

参考答案

第四节  反比例函数的图象与性质（含与一次函数结合）

基础过关

1. C　2. C

3. B　【解析】∵矩形面积公式为S＝xy，∴当S一定时，y＝，即y是x的反比例函数.

4. C 　【解析】分别设正比例函数、反比例函数解析式为y1＝k1x，y2＝，把点A(2，4)分别代入对应解析式，解得k1＝2，k2＝8，∴y1＝2x，y2＝，故A选项错误；根据对称性可知，两个函数图象的另一交点坐标为(－2，－4)，故B选项错误； 当x＜－2或0＜x＜2时，y1＜y2，故C选项正确；正比例函数y1随x的增大而增大，反比例函数y2经过第一、三象限，且在每个象限内随x值的增大而减小，故D选项错误.

5. A　【解析】当a＞0时，b＜0，此时y＝ax－b的图象经过第一、二、三象限，y＝的图象在第一、三象限，选项A符合；当a＜0时，b＞0，此时y＝ax－b的图象经过第二、三、四象限，y＝的图象在第二、四象限，没有符合的选项.故选A.

6. a＞2　【解析】由题意可得a－2＞0，解得a＞2.

7. －2 　【解析】点B是线段OA的中点，∴点B的坐标是(－2，1)，把(－2，1)代入双曲线得k＝－2.

8. －3＜x＜－1　【解析】∵反比例函数y＝(k≠0)的图象经过(3，－1)，∴k＝3×(－1)＝－3，∴反比例函数的解析式为y＝－，∵k＝－3＜0，∴该反比例函数的图象经过第二、四象限，且在每个象限内y随x的增大而增大，当y＝1时，x＝＝－3；当y＝3时，x＝＝－1，∴1＜y＜3时，自变量x的取值范围是－3＜x＜－1.

9. 4　【解析】∵点A(3，n)在双曲线y＝上，∴n＝＝1，∴A(3，1)，∴OC＝3，AC＝1.∵OA的垂直平分线交OC于点M，∴AM＝OM，∴△AMC的周长＝AM＋MC＋AC＝OM＋MC＋AC＝OC＋AC＝3＋1＝4.

10. 解：(1)根据图象上A，B两点的位置可知：xB＞2，

∴－2x＋2＞2，

∴x＜0；

(2)∵x＜0，

∴xC＝－x＞0.

∴点C在第一象限内.

由xB－xC，得－2x＋2－(－x)＝－x＋2.

∵－x＞0，

∴－x＋2＞2.

∴xB＞xC.

∴0＜xC＜xB.

∵反比例函数在第一象限内，y随x的增大而减小，

∴y2＞y1.

11. 解：(1)∵反比例函数y＝的图象经过点B(3，1)，

∴1＝，即k＝3，

∴反比例函数的表达式为y＝.

∵一次函数y＝－x＋b的图象经过点B(3，1)，

∴1＝－3＋b，即b＝4，

∴一次函数的表达式为y＝－x＋4；

(2)由图象可知，1＜a＜3.

12. 解：(1)由题意得xy＝9000，

∴每天生产的套数y(套)与生产的时间x(天)之间是反比例函数关系，

∴y＝(x＞0)；

(2)当y＝300时，x＝30，

答：如果生产车间每天生产300套服装，那么30天可以完成任务；

(3)当x＝10时，y＝900，

答：生产车间每天至少要生产900套服装.

能力提升

1. D　【解析】∵k＜0，∴反比例函数图象位于第二、四象限，当x＝a＜0时，m＞0，当x＝b＞0时，n＜0，∴m＞n.

2. 6　【解析】∵反比例函数y＝的图象上有一点P(2，n)，∴＝n，∵将点P向右平移1个单位，再向下平移1个单位得到点Q，∴平移后点Q的坐标为(3，n－1)，∵点Q也在该函数的图象上，∴＝n－1，列方程组得解得

3.   解：(1)x＜－1或0＜x＜4；

(2)∵点A(－1，4)在y＝的图象上，

∴4＝，

解得k2＝－4，

∴反比例函数的表达式为y＝－.

∵点B(4，n)在反比例函数y＝－的图象上，

∴n＝－＝－1，

∴B(4，－1)，

∵一次函数的图象过A、B两点，

∴

解得

∴一次函数的表达式为y＝－x＋3；

(3)如解图，连接OP，OA，OB，设直线y＝－x＋3与x轴交于点C，

∵当y＝0时，x＝3，

∴点C的坐标为(3，0).

∵S△AOB＝S△AOC＋S△BOC，

∴S△AOB＝×3×4＋×3×1＝.

∵S△AOP∶S△BOP＝1∶2，

∴S△BOP＝S△AOB＝×＝5.

∵点P在线段AB上，设点P的坐标为(m，－m＋3)，

∴S△BOP＝S△POC＋S△BOC＝×3×(－m＋3)＋×3×1＝5，

解得m＝，

∴－m＋3＝－＋3＝，

∴点P的坐标为(，).

第3题解图

满分冲关

1. －　【解析】设点A、B的坐标分别为A(a，－a＋1)，B(b，－b＋1)，∵AB＝2，∴(a－b)2＋(－a＋1＋b－1)2＝(2)2，∴a－b＝±2，由倒影点的定义得A′(，)，B′(，)，又∵点A′、B′都在反比例函数y＝的图象上，∴k＝＝，则a(1－a)＝b(1－b)，整理得(a－b)(1－a－b)＝0，∵a－b＝±2，∴1－a－b＝0，即a＋b＝1，解方程组，与，

得或∴k＝＝－.