



初中数学冀教版八年级下册22.4 矩形图片ppt课件
展开木工朋友在制作窗框后,需要检测所制作的窗框是否是矩形,那么他需要测量哪些数据,其根据又是什么呢?
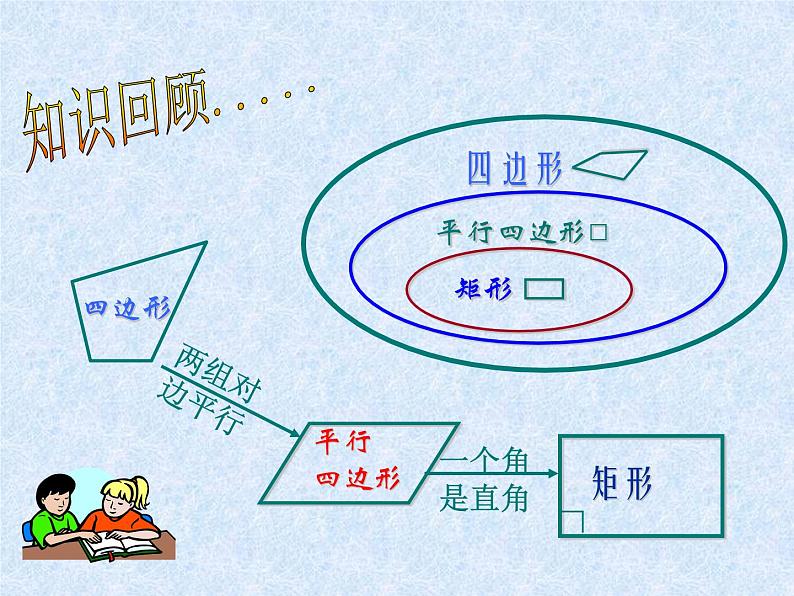
有一个角是直角的平行四边形是矩形。
∴ □ ABCD是矩形
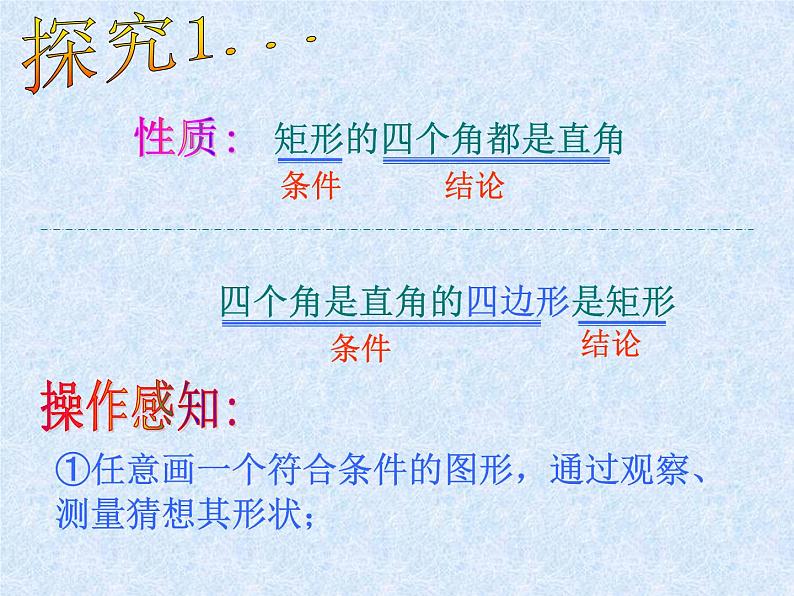
四个角是直角的四边形是矩形
①任意画一个符合条件的图形,通过观察、测量猜想其形状;
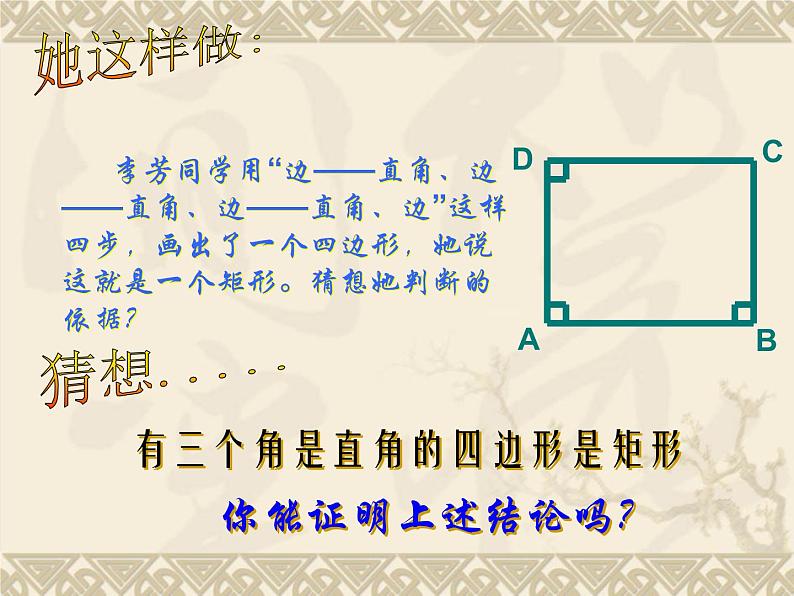
李芳同学用“边——直角、边——直角、边——直角、边”这样四步,画出了一个四边形,她说这就是一个矩形。猜想她判断的依据?
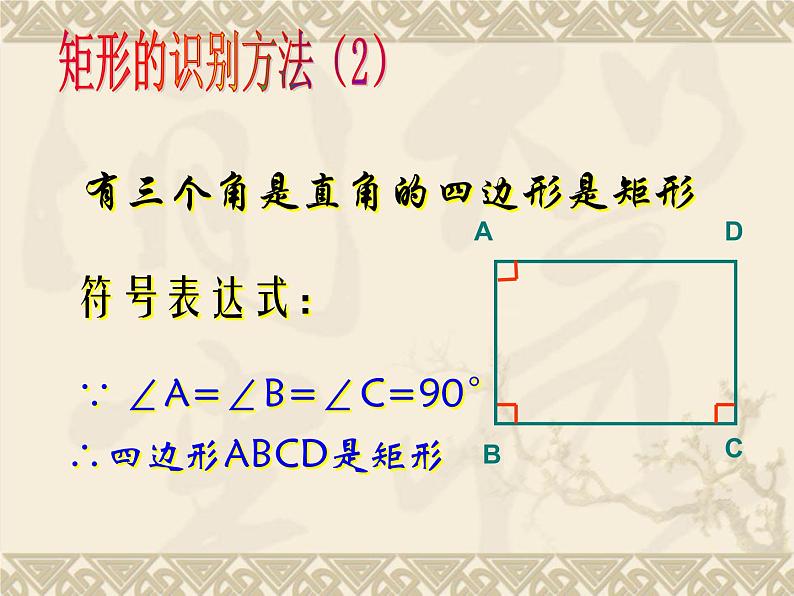
有三个角是直角的四边形是矩形
∵ ∠A=∠B=∠C=90° ∴四边形ABCD是矩形
如图,BD,BE分别是∠ABC与它的邻补角∠CBP的平分线,CE⊥BE,CD⊥BD,E,D为垂足,猜一猜:四边形BECD的形状
∵ BD,BE分别是∠ABC与它的邻补角∠CBP的平分线
又∵ CE⊥BE,CD⊥BD
∴四边形BECD是矩形
例:如图, ABCD四个内角的平分线围成四边形EFGH,猜想四边形EFGH的形状,并说明理由
∵四边形ABCD是平行四边形 ∴∠DAB+∠ABC=180 °
同理:∠EFG=90°、∠FGH=90°
∴四边形EFGH是矩形
∵AE、BE分别平分∠DAB、∠ABC ∴∠EAB+∠EBA=90 °
∴∠AEB=90° 即∠HEF=90°
对角线相等的平行四边形是矩形
②任意画一个符合条件的图形,通过观察、测量猜想其形状确定结论是否正确;
对角线相等的四边形是矩形
∵ 在□ ABCD中,AB=DC, BC=CB, 且AC=DB
∴ △ABC≌ △DCB(SSS)
∵ AB//CD ∴ ∠ABC+∠DCB=180°
∴ ∠ABC=∠DCB=90° 又∵ 四边形ABCD是平行四边形
∴ ∠ABC=∠DCB
命题:对角线相等的平行四边形是矩形。
已知:在□ ABCD,AC=BD求证: □ ABCD是矩形
∵四边形ABCD是平行四边形 且 AC=BD
∴四边形ABCD是矩形
对角线相等的平行四边形是矩形
分别测量出两组对边的长度和一个内角的度数,如果两组对边的长度分别相等,且这个内角是直角,则窗框符合规格
测量出三个内角的度数,如果三个内角都是直角,则窗框符合规格
分别测量出窗框四边和两条对角线的长度,如果窗框两组对边长度、两条对角线的长度分别相等,那么窗框符合规格
分别测量出一组对边的长度和这组同旁内角的度数,如果这组对边的长度相等,且这两个内角都是直角,则窗框符合规格
你在学习平行四边形识别
本节你学到了哪些知识?
对角线相等的平行四边形是矩形 。
(对角线互相平分且相等的四边形是矩形。)
有三个角是直角的四边形是矩形 。
1、已知,如图,□ ABCD和□ ABEC,且BD=BE求证∶ □ ABCD是矩形
∵四边形ABCE是平行四边形
∵四边形ABCD是平行四边形
1、如图,在△ABC中,点D是AC边上的一个动点,过点D作直线MN∥BC,若MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F,
(1)求证:DE=DF
(2)当D运动到何处时, 四边形AECF为矩形? 说明理由
初中冀教版第二十二章 四边形22.4 矩形授课ppt课件: 这是一份初中冀教版第二十二章 四边形22.4 矩形授课ppt课件,共25页。PPT课件主要包含了平行四边形的性质,温故知新,一个角是直角,两组对边分别平行,情景创设,矩形的定义,变化过程,四个角都是直角,对边平行且相等,对角线互相平分且相等等内容,欢迎下载使用。
初中冀教版22.5 菱形教课课件ppt: 这是一份初中冀教版22.5 菱形教课课件ppt,共18页。PPT课件主要包含了情景创设,有一个角是直角,有一组邻边相等,活动一,相信你能解释,菱形的定义,探究菱形的性质,菱形的性质,菱形的面积公式,大显身手等内容,欢迎下载使用。
初中数学冀教版八年级下册22.4 矩形课堂教学ppt课件: 这是一份初中数学冀教版八年级下册22.4 矩形课堂教学ppt课件,共25页。PPT课件主要包含了平行四边形的性质,温故知新,一个角是直角,两组对边分别平行,情景创设,矩形的定义,变化过程,四个角都是直角,对边平行且相等,对角线互相平分且相等等内容,欢迎下载使用。













