冀教版八年级下册22.5 菱形试讲课课件ppt

这是一份冀教版八年级下册22.5 菱形试讲课课件ppt，共16页。PPT课件主要包含了观察思考，活动1菱形的定义，活动2菱形的性质，一组邻边相等，对角线互相平分，一组对边平行且相等，四边形，平行四边形，两组对角分别相等等内容，欢迎下载使用。

（1）图片中有平行四边形吗？（2）这些平行四边形具有哪些特征？其中哪个特征不是平行四边形的性质？
结合上面的观察,你能举出和上述图形具有相同特征的实物图形吗?具有这一特征的平行四边形是什么四边形?
口答下面问题:(1)上面这些图形都是平行四边形吗?(2)上述图形都有一组邻边相等吗?(3)如果平行四边形有一组邻边相等,那么各组邻边都相等吗?
菱形的定义:有一组邻边相等的平行四边形叫做菱形.
【想一想】1.菱形是特殊的平行四边形,它具有一般平行四边形的所有性质.你能列举一些这样的性质吗?2.你认为菱形还具有哪些特殊的性质?请你与同伴交流.
菱形的对边平行且相等,对角相等,对角线互相平分.
【做一做】请同学们用菱形纸片折一折,回答下列问题:1.菱形是轴对称图形吗?如果是,它有几条对称轴?对称轴之间有什么位置关系?2.菱形中有哪些相等的线段?
结论:1.菱形是轴对称图形,有两条对称轴,是菱形对角线所在的直线,两条对角线互相垂直.2.菱形的四条边相等.3.菱形的每条对角线平分一组对角.
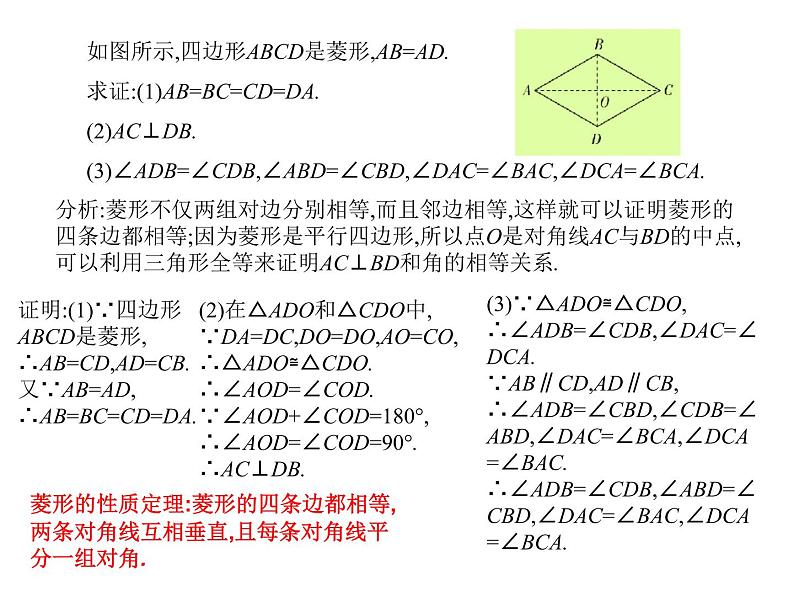
如图所示,四边形ABCD是菱形,AB=AD.求证:(1)AB=BC=CD=DA.(2)AC⊥DB.(3)∠ADB=∠CDB,∠ABD=∠CBD,∠DAC=∠BAC,∠DCA=∠BCA.
分析:菱形不仅两组对边分别相等,而且邻边相等,这样就可以证明菱形的四条边都相等;因为菱形是平行四边形,所以点O是对角线AC与BD的中点,可以利用三角形全等来证明AC⊥BD和角的相等关系.
证明:(1)∵四边形ABCD是菱形,∴AB=CD,AD=CB.又∵AB=AD,∴AB=BC=CD=DA.
(2)在△ADO和△CDO中,∵DA=DC,DO=DO,AO=CO,∴△ADO≌△CDO.∴∠AOD=∠COD.∵∠AOD+∠COD=180°,∴∠AOD=∠COD=90°.∴AC⊥DB.
(3)∵△ADO≌△CDO,∴∠ADB=∠CDB,∠DAC=∠DCA.∵AB∥CD,AD∥CB,∴∠ADB=∠CBD,∠CDB=∠ABD,∠DAC=∠BCA,∠DCA=∠BAC.∴∠ADB=∠CDB,∠ABD=∠CBD,∠DAC=∠BAC,∠DCA=∠BCA.
菱形的性质定理:菱形的四条边都相等,两条对角线互相垂直,且每条对角线平分一组对角.
(教材第142页例1)如图所示,菱形ABCD的周长为16 cm,∠ABC=120°,求对角线BD和AC的长.
解:∵AB+BC+CD+AD=16 cm,∴AB=BC=CD=AD= ×16=4(cm).
∵BD平分∠ABC,∠ABC=120°,∴∠ABD=60°.∴△ABD是等边三角形.∴BD=AB=4 cm.
在Rt△AOB中,OB=2 cm,
[知识拓展]　(1)菱形是特殊的平行四边形,它具有平行四边形的所有性质;(2)菱形的定义既可以看成菱形的性质,也可以看成菱形的判定.
如图所示,四边形ABCD是边长为13 cm的菱形,其中对角线BD的长为10 cm.求: (1)对角线AC的长度;(2)菱形ABCD的面积.
解:(1)∵四边形ABCD是菱形,AC与BD相交于点E,∴∠AED=90°(菱形的对角线互相垂直),DE= BD= ×10=5(cm)(菱形的对角线互相平分).在Rt△AED中,AE= =12(cm).∴AC=2AE=2×12=24(cm).
(2)菱形ABCD的面积=△ABD的面积+△CBD的面积=2×△ABD的面积=2× ×BD×AE=2× ×10×12=120(cm2).
思考：如果例2中,已知菱形ABCD的两条对角线的长度分别为12 cm和10 cm,怎样直接计算出菱形的面积?
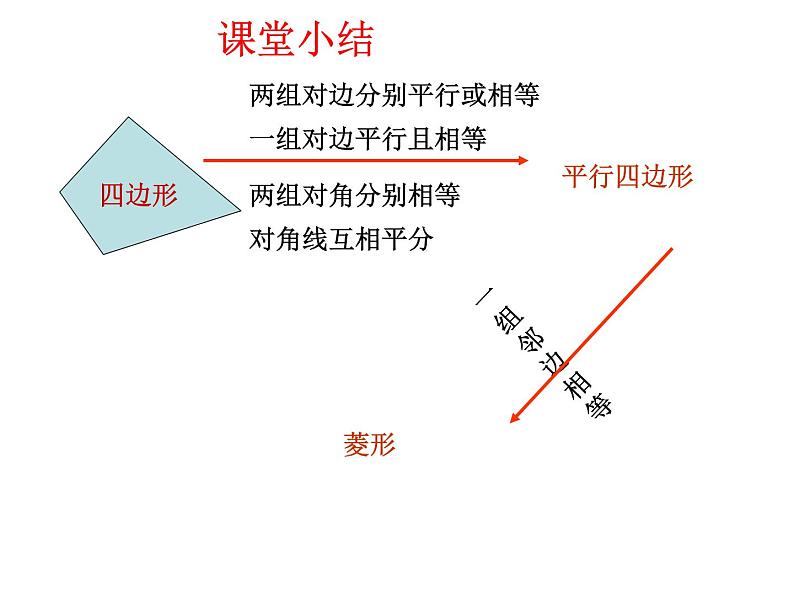
两组对边分别平行或相等
课堂小结
1.如图所示,菱形ABCD中,AB=5,∠BCD=120°,则对角线AC的长是(　　)A.20 B.15 C.10D.5
解析:因为四边形ABCD是菱形,所以AB=CB,AB∥DC,所以∠ABC=180°-∠BCD=180°-120°=60°,所以△ABC是等边三角形,所以AC=AB=5.故选D.
2.(2016·莆田中考)菱形具有而一般平行四边形不具有的性质是(　　)A.对边相等 B.对角相等C.对角线互相平分D.对角线互相垂直
解析:菱形具有的性质为:对边相等,对角相等,对角线互相平分,对角线互相垂直;一般平行四边形具有的性质为:对边相等,对角相等,对角线互相平分.所以菱形具有而一般平行四边形不具有的性质是:对角线互相垂直.故选D.
3.如图所示,菱形ABCD的对角线AC,BD相交于O点,E,F分别是AB,BC边上的中点,连接EF.若EF= ,BD=4,则菱形ABCD的周长为(　　)A.4B.4 C.4 D.28
解析:∵E,F分别是AB,BC边上的中点,EF= ,∴AC=2EF=2 .∵四边形ABCD是菱形,∴AC⊥BD,OA= AC= ,OB= BD=2,∴AB= ,∴菱形ABCD的周长为4 .故选C.
4.如图所示,菱形ABCD的周长为8 cm,高AE的长为 cm,则对角线AC和BD的长度之比为(　　)A.1∶2 B.1∶3C.1∶ D.1∶
解析:设AC,BD相交于点O,∵菱形ABCD的周长为8cm,∴AB=BC=2 cm.∵高AE的长为 cm,∴BE= =1(cm),∴CE=BE=1 cm,∴AC=AB=2 cm,∵OA=1 cm,AC⊥BD,∴OB = (cm),∴BD=2OB=2 cm,∴AC∶BD=1∶ .故选D.
5.如图所示,菱形ABCD的周长为8 cm.∠BAD=60°,则AC=　　　　cm. 
解析:因为菱形ABCD的周长为8 cm,所以AB=2 cm,AB=AD.又因为∠BAD=60°,所以△ABC是等边三角形,所以BD=AB=2 cm,所以OA= (cm).所以AC=2 cm.故填2 .
6.如图所示,AC是菱形ABCD的对角线,点E,F分别在AB,AD上,且AE=AF.求证CE=CF.
解析:由四边形ABCD是菱形,可得∠EAC=∠FAC,又由AE=AF,AC为公共边,即可证得△ACE≌△ACF,则可得CE=CF.
证明:∵四边形ABCD是菱形,∴∠EAC=∠FAC.在△ACE和△ACF中,
∴△ACE≌△ACF(SAS).∴CE=CF.
7.如图所示,菱形ABCD的对角线AC,BD相交于点O,点E,F分别是边AB,AD的中点.(1)请判断△OEF的形状,并证明你的结论;(2)若AB=13,AC=10,请求出线段EF的长.
解析:(1)利用菱形的性质结合直角三角形斜边上的中线等于斜边的一半,进而得到OE=OF,可判断△OEF的形状;(2)利用勾股定理得出BO的长,再利用三角形的中位线定理得出EF的长.
解:(1)△OEF是等腰三角形.证明:∵四边形ABCD是菱形,∴AB=AD,AC⊥BD.∵点E,F分别是边AB,AD的中点,∴EO= AB,OF= AD,∴EO=FO,∴△OEF是等腰三角形.
(2)∵四边形ABCD是菱形,AC=10,∴AO=5,∠AOB=90°,∴BO= =12,∴BD=24.∵点E,F分别是边AB,AD的中点,∴EF= BD,∴EF=12.
8.如图所示,在△ABC中,AB=AC,四边形ADEF是菱形,求证BE=CE.
解析:根据四边形ADEF是菱形,得DE=EF,AB∥EF,DE∥AC,可证明△DBE≌△FEC,即可得出BE=CE.
证明:∵四边形ADEF是菱形,∴DE=EF,AB∥EF,DE∥AC,∴∠C=∠BED,∠B=∠CEF.∵AB=AC,∴∠B=∠C,∴∠BED=∠CEF,
在△DBE和△FEC中,∴△DBE≌△FEC,∴BE=CE.
9.如图所示,已知菱形ABCD,AB=AC,E,F分别是BC,AD的中点,连接AE,CF. (1)求证四边形AECF是矩形;(2)若AB=6,求菱形的面积.
解析:(1)首先证明△ABC是等边三角形,进而得出∠AEC=90°,四边形AECF是平行四边形,即可得出答案;(2)利用勾股定理得出AE的长,进而求出菱形的面积.
证明:(1)∵四边形ABCD是菱形,∴AB=BC.又∵AB=AC,∴AB=AC=BC.∴△ABC是等边三角形.∵E是BC的中点,∴AE⊥BC,∴∠AEC=90°.
∵E,F分别是BC,AD的中点,∴AF= AD,EC= BC.∵四边形ABCD是菱形,∴AD∥BC且AD=BC,∴AF∥EC且AF=EC,∴四边形AECF是平行四边形.又∵∠AEC=90°,∴四边形AECF是矩形.
解:(2)在Rt△ABE中,AE= ,所以
10.如图所示,在△ABC中,∠ACB=90°,D,E分别是BC,BA的中点,连接DE,点F在DE的延长线上,且AF=AE. (1)求证四边形ACEF是平行四边形;(2)若四边形ACEF是菱形,求∠B的度数.
解析:(1)根据直角三角形斜边上的中线等于斜边的一半可得CE=AE=BE,从而得到AF=CE,再根据等腰三角形“三线合一”的性质可得∠1=∠2,根据等边对等角可得∠F=∠3,对顶角相等得∠1=∠3,然后得到∠2=∠F,再根据同位角相等,两直线平行得到CE∥AF,然后由一组对边平行且相等的四边形是平行四边形得证;(2)根据菱形的四条边都相等可得AC=CE,然后得到AC=CE=AE,从而得到△AEC是等边三角形,再根据等边三角形的每一个内角都是60°求出∠CAE=60°,然后根据直角三角形的两锐角互余解答.