



初中数学冀教版八年级下册22.5 菱形获奖课件ppt
展开由对角线的位置关系判定菱形由边的关系判定菱形
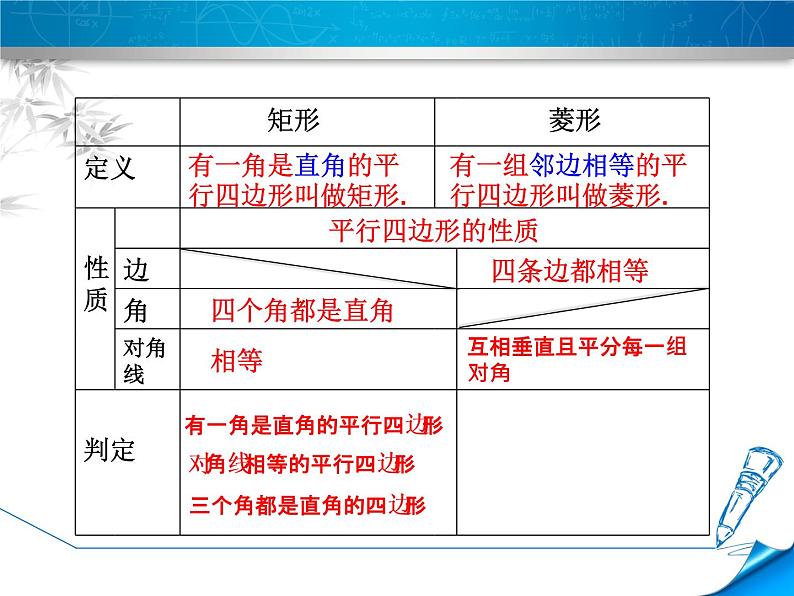
想一想:1.菱形、矩形的定义?2.它们分别比平行四边形多了哪些性质?3.怎样判定一个四边形是矩形?
有一角是直角的平行四边形叫做矩形.
有一组邻边相等的平行四边形叫做菱形.
互相垂直且平分每一组对角
有一角是直角的平行四边形
对角线相等的平行四边形
三个角都是直角的四边形
同学们想一想,我们在学习平行四边形的判定和矩形的判定时,我们是如何到的它们的判定方法呢?那么类比着它们,菱形的判定方法是什么?
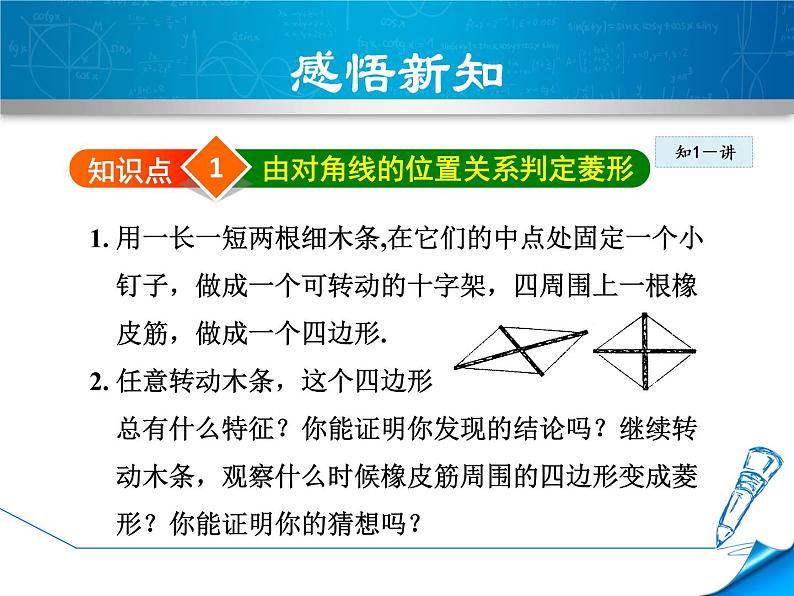
由对角线的位置关系判定菱形
1. 用一长一短两根细木条,在它们的中点处固定一个小 钉子,做成一个可转动的十字架,四周围上一根橡 皮筋,做成一个四边形.2. 任意转动木条,这个四边形 总有什么特征?你能证明你发现的结论吗?继续转 动木条,观察什么时候橡皮筋周围的四边形变成菱 形?你能证明你的猜想吗?
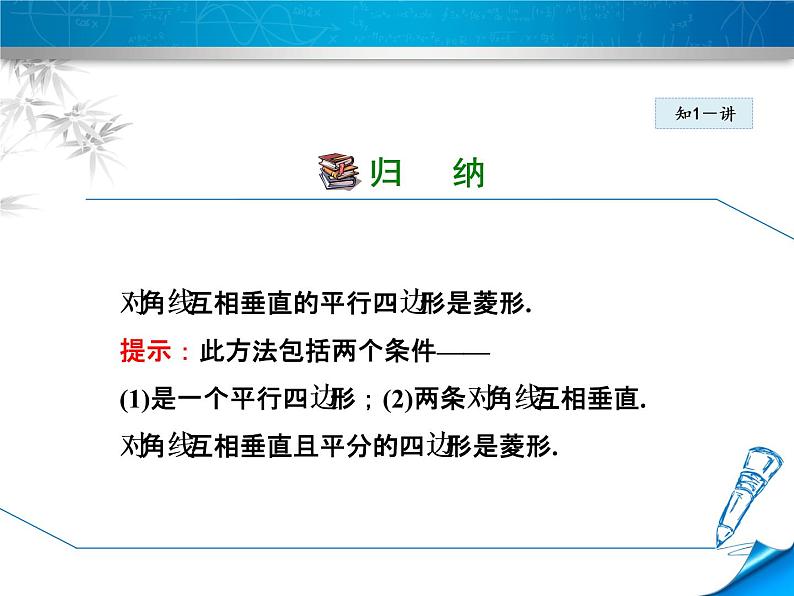
猜想:对角线互相垂直的平行四边形是菱形.3. 这个命题的前提是什么?结论是什么?用几何语言表示命题如下:已知:在□ABCD中,对角线AC⊥BD,求证:□ABCD是菱形.分析:我们可根据菱形的定义来证明这个平行四边形是菱形,由平行四边形的性质得到BO=DO,由∠AOB=∠AOD=90º及AO=AO,得△AOB≌△AOD,可得到AB=AD (或根据线段垂直平分线性质定理,得到AB=AD) ,最后证得□ABCD是菱形.
对角线互相垂直的平行四边形是菱形.提示:此方法包括两个条件——(1)是一个平行四边形;(2)两条对角线互相垂直.对角线互相垂直且平分的四边形是菱形.
例1 如图,在平行四边形ABCD中,对角线AC,BD相交于点O,过点O作直线EF⊥BD,分别交AD,BC于点E和点F,连接BE,DF. 求证:四边形BEDF是菱形.
若要证明四边形BEDF是菱形,需要先证明四边形BEDF是平行四边形,而由题意易知DE∥BF,只需要证明DE=BF,即可判定四边形BEDF是平行四边形,证明DE=BF可通过证明△OED≌△OFB来实现.
∵四边形ABCD是平行四边形,∴OB=OD,AD∥BC.∴∠EDO=∠FBO,∠OED=∠OFB.∴△OED≌△OFB. ∴DE=BF.又∵DE∥BF,∴四边形BEDF是平行四边形.∵EF⊥BD,∴四边形BEDF是菱形.
证明一个四边形是菱形时,若已知要证的四边形的对角线互相垂直,则要考虑证明这个四边形是平行四边形.
已知:如图,在▱ABCD中,O为对角线AC的中点,过点O作AC的垂线与边AD,BC分别交于点E,F. 求证:四边形AFCE是菱形.
∵O为AC的中点,EF⊥AC,∴AE=EC,AF=FC,在▱ABCD中,∵AD∥BC,∴∠AEO=∠CFO,∠EAO=∠OCF,在△AEO与△CFO中,∴△AEO≌△CFO,∴AE=CF.∴AE=EC=CF=FA.∴四边形AFCE是菱形.
【中考·海南】如图,四边形 ABCD 是轴对称图形,且直线 AC 是对称轴,BD与AC交于点O,AB∥CD,则下列结论:①AC⊥BD;②AD∥ BC;③四边形 ABCD 是菱形;④△ABD≌△CDB.其中正确的是____________(只填写序号).
【中考·泰安】如图,四边形ABCD是平行四边形,点E是边CD上一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论:①BE平分∠CBF;②CF平分∠DCB;③BC=FB; ④PF=PC,其中正确结论的个数为( )A.1 B.2 C.3 D.4
如图,画两条等长的线段AB,AD.分别以点B, D为圆心,AB为半径画弧,两弧相交于点C连接BC,CD.得到四边形ABCD.四边形ABCD是菱形吗?
事实上,我们有:四条边相等的四边形是菱形.现在,我们来证明这个结论.已知:如图,在四边形ABCD中,AB=BC=CD=DA.求证:四边形是菱形.证明:∵AB=CD.且BC=AD,∴四边形ABCD是平行四边形.又∵AB=AD.∴四边形ABCD是菱形.
四条边相等的四边形是菱形.
例2 已知:如图,在△ABC中,AD是∠BAC的平分线,DE∥AC,交AB于点E,DF∥AB,交AC于点F.求证:四边形AEDF是菱形.
∵ DE∥AC, DF∥AB,∴四边形AEDF是平行四边形.∴∠1=∠3.又∵∠1=∠2,∴∠2=∠3.∴AE=DE.∴四边形AEDF是菱形.
能证明四边形是平行四边形时,可以先证明四边形是平行四边形,然后证明有一组邻边相等来证明四边形是菱形 .
1 如图,在△ABC中,AB=AC,画出点A关于BC的对称点A'.请用两种不同的方法证明四边形ABA'C是菱形.
如图,E是菱形ABCD的边AD的中点,EF⊥ BD于点H,交BC延长线于点F,交DC于点G.求证:DC与EF互相平分.
连接AC,则AC⊥BD,又因为EF⊥BD,∴AC∥EF.∵E是AD的中点,∴G是DC中点.易得△DEG≌△CFG,∴EG=FG,∴DC与EF互相平分.
已知:如图,四边形ABCD是菱形,两条对角线交于点O,DE为∠ADB的平分线,交AC于点E,DF为∠CDB的平分线,交AC于点F,连接BE,BF. 求证:四边形DEBF是菱形.
∵四边形ABCD是菱形,AC、BD是其两条对角线,∴EF垂直平分DB,∴ED=EB,DF=BF.∵DE、DF分别平分∠ADB,∠CDB,∠ADB=∠CDB,∴∠ADE=∠CDF.在△ADE和△CDF中,∴△ADE≌△CDF,∴DE=DF,∴DE=DF=BE=BF.∴四边形DEBF是菱形.
例3 如图,在四边形ABCD中,AD∥BC,AB=CD, 点E,F,G,H分别是AD,BD,BC,AC的中 点.试说明:四边形EFGH是菱形.
由于点E,F,G,H分别是AD,BD,BC,AC的中点,可知EH,HG,GF,FE分别是△ACD,△ABC,△BCD,△ABD的中位线,又∵AB=CD,∴EH=HG=GF=FE,根据“四条边相等的四边形是菱形”可得四边形EFGH是菱形.
∵点E,H分别为AD,AC的中点,∴EH为△ACD的中位线,∴EH= CD.同理可证:EF= AB,FG= CD,HG= AB.∵AB=CD,∴EH=EF=FG=HG,∴四边形EFGH是菱形.
有较多线段相等的条件时,我们可考虑通过证明四条边相等来证明这个四边形是菱形.注意:本例也可以通过先证四边形EFGH是平行四边形,再证一组邻边相等,只不过步骤复杂一点,读者不妨试一试.
如图在▱ABCD中,∠D=60°,以顶点A为圆心,AB为半径画弧,交BC于点E,交AD于点F.请你指出图中的等腰三角形、平行四边形和菱形.
△ABE,△AEF是等腰三角形.四边形ABCD、四边形ABEF、四边形CDFE是平行四边形,四边形ABEF是菱形.
如图,在菱形ABCD中,∠BAD=60°,M为AB中点,P为对角线AC上的一个动点,PM+PB的最小值是3. 求AB的长.
作点M关于AC对称的点M′,则M′在边AD上.且M′为AD的中点,连接BM′,易得BM′的长为PM+PB的最小值,∴BM′=3. 连接BD,∵AB=AD,∠BAD=60°,∴△ABD为等边三角形.∴∠ABM′=30°,∠AM′B=90°,∴AM′= AB,AB2-AM′2=BM′2=9,∴AB=2 .
如图,绿丝带下部重叠部分是什么图形?请说明理由.
解:菱形. 理由略.
如图,四边形ABCD的对角线AC,BD互相垂直,则下列条件能判定四边形ABCD为菱形的是( )A.BA=BC B.AC,BD互相平分C.AC=BD D.AB∥CD
【中考·河南】如图,在▱ABCD中,对角线AC,BD相交于点O,添加下列条件不能判定▱ABCD是菱形的只有( )A.AC⊥BD B.AB=BC C.AC=BD D.∠1=∠2
如图,将▱ABCD沿AE翻折,使点B恰好落在AD上的点F处,则下列结论不一定成立的是( )A.AF=EF B.AB=EF C.AE=AF D.AF=BE
如图,在△ABC中,点D是边BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列说法正确的是( )A.若AD⊥BC,则四边形AEDF是矩形B.若AD垂直平分BC,则四边形AEDF是矩形C.若BD=CD,则四边形AEDF是菱形D.若AD平分∠BAC,则四边形AEDF是菱形
如图,四边形ABCD的四边相等,且面积为120 cm2,对角线AC =24 cm,则四边形ABCD的周长为 ( )A.52 cm B.40 cm C.39 cm D.26 cm
如图,在△ABC中,AD是角平分线,DE∥AC交AB于点E,DF∥AB交AC于点F.如果AE=4 cm,那么四边形AEDF的周长为( )A.12 cm B.16 cm C.20 cm D.22 cm
如图,分别以Rt△ABC的斜边AB和直角边AC为边向△ABC外作等边三角形ABD和等边三角形ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠BAC=30°.给出以下结论:①EF⊥AC; ②四边形ADFE为菱形;③AD=4AG; ④FH= BD.其中正确的结论是( )A.①②③ B.①②④ C.①③④ D.②③④
下列命题:①四边都相等的四边形是菱形;②两组邻边分别相等的四边形是菱形;③对角线互相垂直的平行四边形是菱形;④对角线相等的四边形是菱形;⑤一条对角线平分一组对角的平行四边形是菱形.其中正确的是__________(填序号).
易错点:臆造菱形的判定方法导致出错
数学人教版18.2.2 菱形优秀课件ppt: 这是一份数学人教版18.2.2 菱形优秀课件ppt,共24页。PPT课件主要包含了你能证明这一猜想吗,菱形的判定定理,即AC⊥BD,∴ACBD,请补充完整的证明过程,cm2等内容,欢迎下载使用。
冀教版22.5 菱形图文ppt课件: 这是一份冀教版22.5 菱形图文ppt课件,共14页。PPT课件主要包含了类比猜想,活动与实践,猜想与验证,归纳与总结,理解与辨析,理解与应用,拓展与提升,问题回归等内容,欢迎下载使用。
数学八年级下册22.5 菱形习题ppt课件: 这是一份数学八年级下册22.5 菱形习题ppt课件,共29页。PPT课件主要包含了答案显示,见习题等内容,欢迎下载使用。













