八年级上数学课件阶段核心技巧 用全等三角形证明五种常见结论的证明技巧_冀教版

这是一份初中数学冀教版八年级上册本册综合教学演示ppt课件，共17页。PPT课件主要包含了答案显示，见习题等内容，欢迎下载使用。

1．【中考•陕西】如图，点A，E，F，B在直线l上，AE＝BF，AC∥BD，且AC＝BD，求证：CF＝DE.
证明：∵AE＝BF，∴AE＋EF＝BF＋EF，即AF＝BE.∵AC∥BD，∴∠CAF＝∠DBE.又∵AC＝BD，∴△ACF≌△BDE(SAS)．∴CF＝DE.
2．如图，在正方形ABCD中，点E，F分别在边AB，BC上，AF＝DE，AF和DE交于点G.(1)观察图形，写出图中所有与∠AED相等的角(∠CDE除外)；
解：∠DAG、∠AFB与∠AED相等．
(2)选择图中与∠AED相等的任意一个角(∠CDE除外)加以证明．
∴△DAE≌△ABF，∴∠ADE＝∠BAF.∵∠DAG＋∠BAF＝90°，∠ADE＋∠AED＝90°，∴∠DAG＝∠AED.
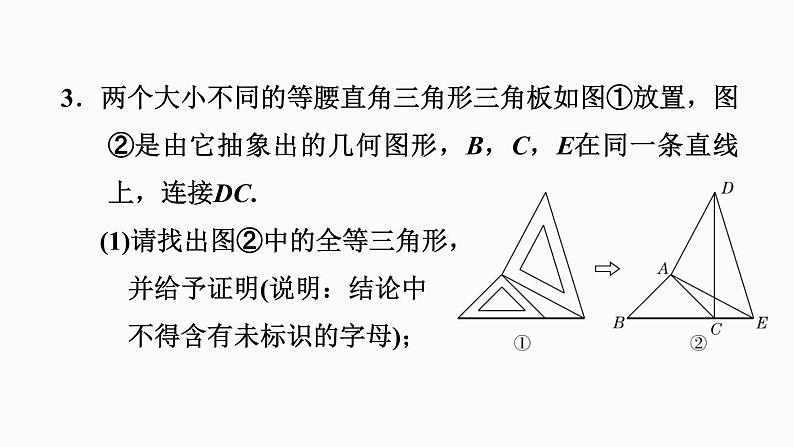
3．两个大小不同的等腰直角三角形三角板如图①放置，图②是由它抽象出的几何图形，B，C，E在同一条直线上，连接DC.(1)请找出图②中的全等三角形， 并给予证明(说明：结论中 不得含有未标识的字母)；
解：△ABE≌△ACD，证明如下：∵△ABC与△AED均为等腰直角三角形，∴AB＝AC，AE＝AD，∠BAC＝∠EAD＝90°，∴∠BAC＋∠CAE＝∠EAD＋∠CAE，即∠BAE＝∠CAD，∴△ABE≌△ACD.
证明：由(1)知△ABE≌△ACD，则∠ACD＝∠ABE.又∵∠ABC＋∠ACB＝90°，∴∠ACD＋∠ACB＝90°，∴∠BCD＝90°.即DC⊥BE.
(2)求证：DC⊥BE.
4．如图，已知AE∥DF，CE∥BF，AB＝CD，求证：BE∥CF.
证明：∵AE∥DF，∴∠A＝∠D.∵CE∥BF，∴∠ECA＝∠FBD.∵AB＝CD，∴AC＝DB，∴△AEC≌△DFB(ASA)，∴EC＝BF.又∵∠ECA＝∠FBD，BC＝CB，∴△ECB≌△FBC(SAS)，∴∠EBC＝∠FCB，∴BE∥CF.
5．如图，在△ABC中，AC＝BC，∠ACB＝90°，D为BC延长线上一点，BF⊥AD于F，交AC于E.(1)求证：BE＝AD；(2)过C点作CM∥AB交AD于M，连接EM，求证：BE＝AM＋EM.
【点拨】本题运用了等线段代换法解决线段的和差问题，解决三条线段之间的和差问题一般通过全等转化为证两线段相等．
(1)求证：BE＝AD；
(2)过C点作CM∥AB交AD于M，连接EM，求证：BE＝AM＋EM.
【点拨】本题运用了截长法解决线段的和差问题．截长法是在第三条线段上截取一条线段等于第一条线段，证余下的线段等于第二条线段．本题在AE上截取AF＝AB，证EF＝DE.
6．如图，在四边形ABDE中，C是BD边的中点．若AC平分∠BAE，∠ACE＝90°，猜想线段AE，AB，DE满足的数量关系，并证明．
解：AE＝AB＋DE.证明：如图，在AE上截取AF＝AB，连接CF.∵AC平分∠BAE，∴∠BAC＝∠CAF.又∵AC＝AC，∴△BAC≌△FAC，∴BC＝FC，∠ACB＝∠ACF.∵∠ACE＝90°，∴∠ACF＋∠FCE＝90°，∠ACB＋∠DCE＝90°，∴∠FCE＝∠DCE.∵C为BD边的中点，∴BC＝DC，∴DC＝FC.又∵CE＝CE，∴△FCE≌△DCE，∴DE＝FE，∴AE＝AF＋FE＝AB＋DE.