数学八年级下册2 矩形的性质与判定评课ppt课件

这是一份数学八年级下册2 矩形的性质与判定评课ppt课件，共15页。PPT课件主要包含了证明命题的一般步骤，四边形之间有何关系，求证ACBD，∵BCCB，∴ACDB，BE等于AC的一半，求矩形对角线的长，∴ACBD且，∵∠DAB900，∴∠ABC900等内容，欢迎下载使用。
(1)理解题意:分清命题的条件(已知),结论(求证);
(2)根据题意,画出图形;
(3)结合图形,用符号语言写出“已知”和“求证”;
(4)分析题意,探索证明思路(由“因”导“果”,执“果”索“因”);
(5)依据思路,运用数学符号和数学语言条理清晰地写出证明过程;
(6)检查表达过程是否正确,完善.
定理:平行四边形的对边相等.
证明后的结论,以后可以直接运用.
∵四边形ABCD是平行四边形.∴AB=CD,BC=DA.
定理:平行四边形的对角相等.
∵四边形ABCD是平行四边形.∴∠A=∠C, ∠B=∠D.
定理:平行四边形的对角线互相平分.
∵四边形ABCD是平行四边形.∴CO=AO,BO=DO.
定理:夹在两条平等线间的平等线段相等.
∵MN∥PQ,AB∥CD,∴AB=CD.
定理:两组对边分别相等的四边形是平行四边形.
定理:一组对边平行且相等的四边形是平行四边形.
定理:对角线互相平分的四边形是平行四边形.
定理:两组对角分别相等的四边形是平行四边形的.
∵AB=CD,AD=BC,∴四边形ABCD是平行四边形.
∵AB∥CD,AB=CD,∴四边形ABCD是平行四边形.
∵AO=CO,BO=DO,∴四边形ABCD是平行四边形.
∵∠A=∠C,∠B=∠D.∴四边形ABCD是平行四边形.
特殊的平行四边形之间呢？
还记得它们与平行四边形的关系吗?
能用一张图来表示它们之间的关系吗?
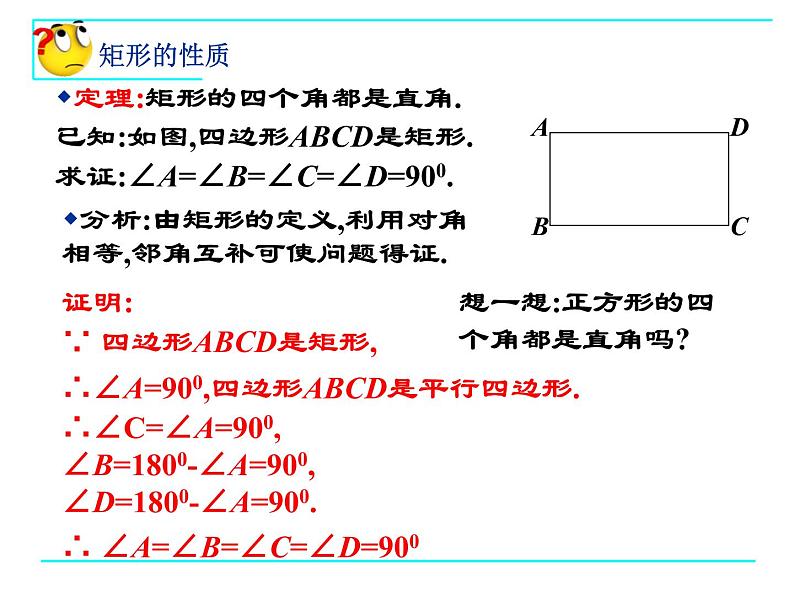
定理:矩形的四个角都是直角.
已知:如图,四边形ABCD是矩形.
分析:由矩形的定义,利用对角相等,邻角互补可使问题得证.
∵ 四边形ABCD是矩形,
∴∠A=900,四边形ABCD是平行四边形.
∴∠C=∠A=900,∠B=1800-∠A=900, ∠D=1800-∠A=900.
求证:∠A=∠B=∠C=∠D=900.
∴ ∠A=∠B=∠C=∠D=900
想一想:正方形的四个角都是直角吗?
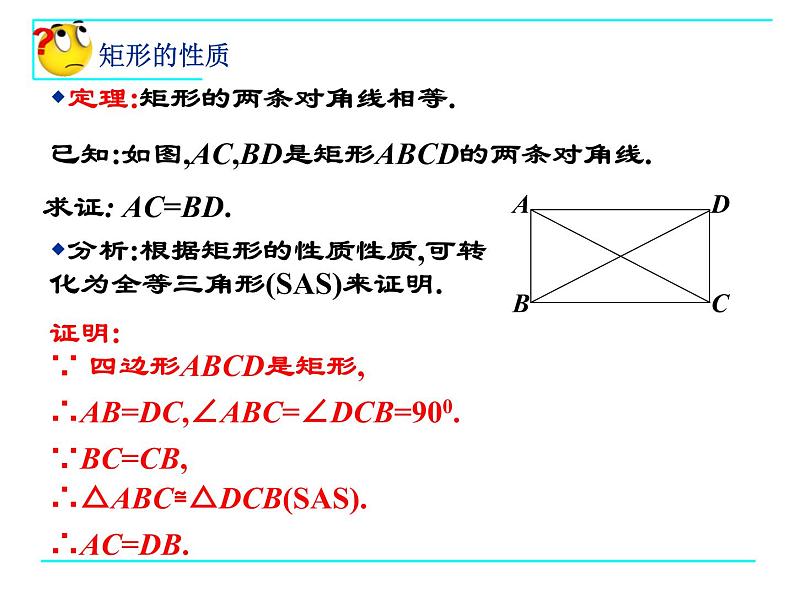
定理:矩形的两条对角线相等.
已知:如图,AC,BD是矩形ABCD的两条对角线.
∴AB=DC,∠ABC=∠DCB=900.
分析:根据矩形的性质性质,可转化为全等三角形(SAS)来证明.
∴△ABC≌△DCB(SAS).
议一议:设矩形的对角线AC与BD交于点E,那么,BE是Rt△ABC中一条怎样的特殊线段?
它与AC有什么大小关系?为什么?
由此可得推论:直角三角形斜边上的中线等于斜边的一半.
BE是Rt△ ABC中斜边AC上的中线.
∵ AC=BD,BE=DE,
已知:如图,AC,BD是矩形ABCD的两条对角线,AC,BD相交于点O,∠AOD=1200,AB=2.5cm.
∵四边形ABCD是矩形,
∴BD=2AB=2×2.5=5(cm).
∵∠AOD=1200,
你认为例1还可以怎么去解？
定理:有三个角是直角的四边形是矩形.
已知:如图,在四边形ABCD中, ∠A=∠B=∠C=900.
分析:利用同旁内角互补,两直线平行来证明四边形是平行四边形,可使问题得证.
∵ ∠A=∠B=∠C=900,
∴∠A+∠B=1800,∠B+∠C=1800.
∴AD∥BC,AB∥CD.
求证:四边形ABCD是矩形.
∴四边形ABCD是平行四边形.
∴四边形ABCD是矩形.
定理:对角线相等的平行四边形是矩形.
已知:如图,在□ABCD中,对角线AC=BD.
分析:要证明□ABCD是矩形,只要证明有一个角是直角即可.
∴AB=CD,AB∥CD.
∵AC=DB,BC=CB,
∴ △ABC≌△DCB.
∴∠ABC=∠DCB.
∵四边形ABCD是平行四边形.
∵∠ABC+∠DCB=1800.
定理:如果一个三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.
求证:△ABC是直角三角形
分析:要证明△ABC是直角三角形,可以点A,B,C构造平行四边形,然后证明其对角线相等,即可证明是矩形.
证明:延长CD到E,使DE=DC,连接AE,BE.
∴四边形ACBE是平行四边形.
∵AB=2CD,CE=2CD,
∴四边形ACBE是矩形.
∵ AD=BD,CD=ED,
∴△ABC是直角三角形.
推论(直角三角形性质):直角三角形斜边上的中线等于斜边的一半.
∴∠A=∠B=∠C=∠D=900.
∵AC,BD是矩形ABCD的两条对角线.
在△ABC中,∠ACB=900,∵AD=BD,
∵∠A=∠B=∠C=900,
∵AC,BD是□ABCD的两条对角线,且AC=DB.
在△ABC中,∵AD=BD=CD,