

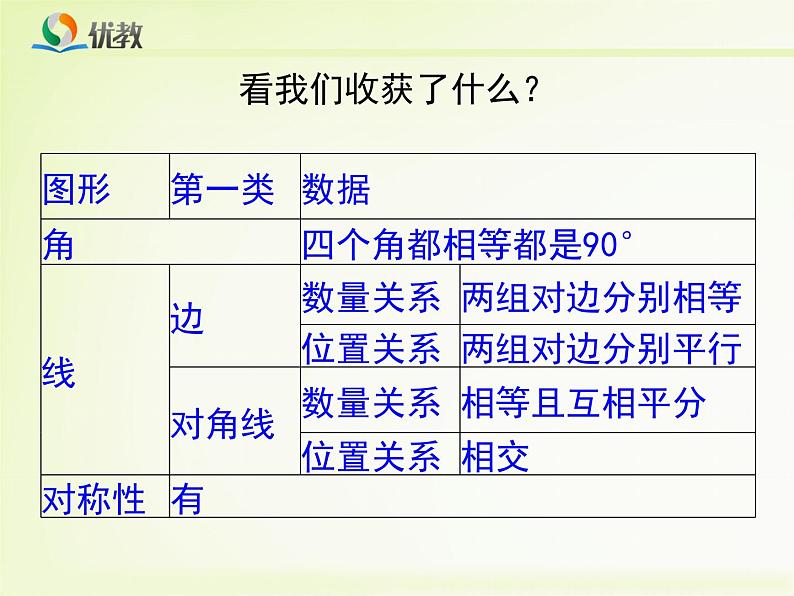




初中数学鲁教版 (五四制)八年级下册3 正方形的性质与判定授课课件ppt
展开第二类图形就是正方形,我们给出定义:有一组邻边相等的矩形叫做正方形.
议一议:(1)正方形是菱形吗?(2)你认为正方形有哪些性质?
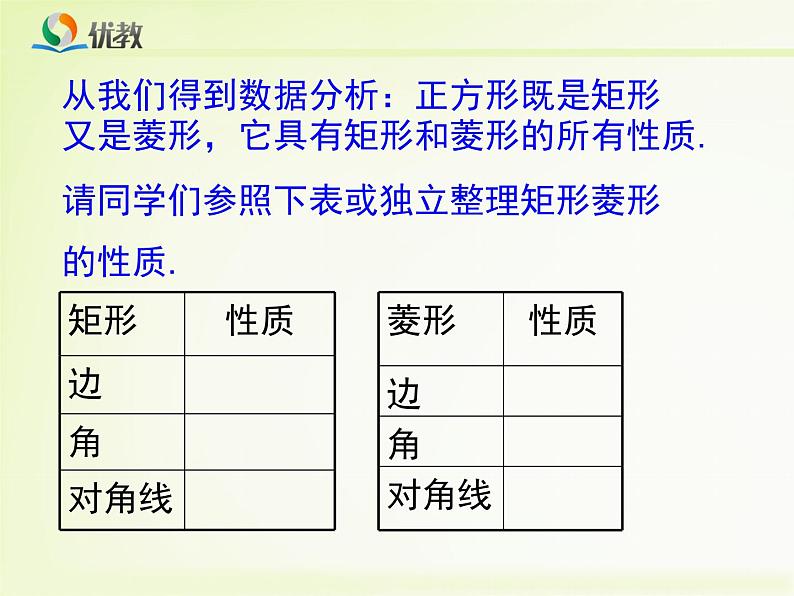
从我们得到数据分析:正方形既是矩形又是菱形,它具有矩形和菱形的所有性质.
请同学们参照下表或独立整理矩形菱形的性质.
于是我们得到了正方形的两条定理:定理 正方形的四个角都是直角,四条边都相等定理正方形的对角线相等且互相垂直平分
想一想:正方形有几条对称轴
解析:正方形有4条对称轴.经验层面:可通过折叠.分析层面:正方形具有矩形、菱形的所有性质,所以必然具有矩形过每组对边中点的对称轴和菱形过对角线的对称轴.
例1:如图1-18,在正方形ABCD中,E为CD上一点,F为BC边延长线上一点,且CE=CF.BE与DF之间有怎样的关系?请说明理由.
解:BE=DF,且BE⊥DF.理由如下:
(1)∵四边形ABCD是正方形.∴BC=DC,∠BCE=90°(正方形的四条边都相等,四个角都是直角).∴∠DCF=180°-∠BCE=180°-90°=90°.∴∠BCE=∠DCF.又∵CE=CF.∴△BCE≌△DCF.∴BE=DF.
(2)延长BE交DE于点M,(如图1-19).∵△BCE≌△DCF.∴∠CBE=∠CDF.∵∠DCF=90°.∴∠CDF+∠F=90°.∴∠CBE+∠F=90°.∴∠BMF=90°.∴BE⊥DF.
平行四边形、菱形、矩形、正方形之间有么关系?你能用一个你喜欢的方式直观地示它们之间的关系吗 ?与同伴交流.
1:如图,在正方形ABCD中,对角线AC与BD相交于点O,图中有多少个等腰三角形?2:如图,在正方形ABCD中,点F为对角线AC上一点,连接BF,DF。你能找出图中的全等三角形吗?选择其中一对进行证明.
1:解:图中共有8个等腰三角形.2:解:图中的全等三角形共有3对, 分别是△ADC与ABC, △FCD与FCB, △FAD与△FAB.
选择△FAD≌△FAB证明,过程如下:
∵正方形ABCD,∴AD=AB,∠DAF=∠BAF,又∵AF=AF∴△FAD≌△FAB.
1:正方形的性质:包括边、角、对角线以及对称性.2:将平行四边形、矩形、菱形、正方形之间的联系.3:建立起适合自己的知识结构并内化为自己数学品质的一部分.
课本P22A-1层作业:习题1.7A-2层作业:知识技能T1,T2B层作业:数学理解T3
初中数学第六章 特殊平行四边形3 正方形的性质与判定完整版课件ppt: 这是一份初中数学第六章 特殊平行四边形3 正方形的性质与判定完整版课件ppt,共35页。PPT课件主要包含了逐点学练,本节小结,作业提升,本节要点,学习流程,知识点,正方形的定义,正方形的性质,正方形的判定,邻边相等等内容,欢迎下载使用。
鲁教版 (五四制)八年级下册3 正方形的性质与判定教案配套ppt课件: 这是一份鲁教版 (五四制)八年级下册3 正方形的性质与判定教案配套ppt课件,共19页。PPT课件主要包含了这些物体是什么图形,这还是正方形吗,失踪的正方形,相信自己加油,①④或②④,透过变化看本质等内容,欢迎下载使用。
初中数学人教版八年级下册18.2.3 正方形教学ppt课件: 这是一份初中数学人教版八年级下册18.2.3 正方形教学ppt课件,共23页。PPT课件主要包含了平行四边形再认识,讲授新课,问题引入,正方形,邻边相等,一个角是直角,正方形定义,归纳总结,证一证,轴对称图形等内容,欢迎下载使用。













