

专题08 椭圆及其方程(重难点突破)原卷版-高二上(新教材人教A版)
展开专题08 椭圆及其方程
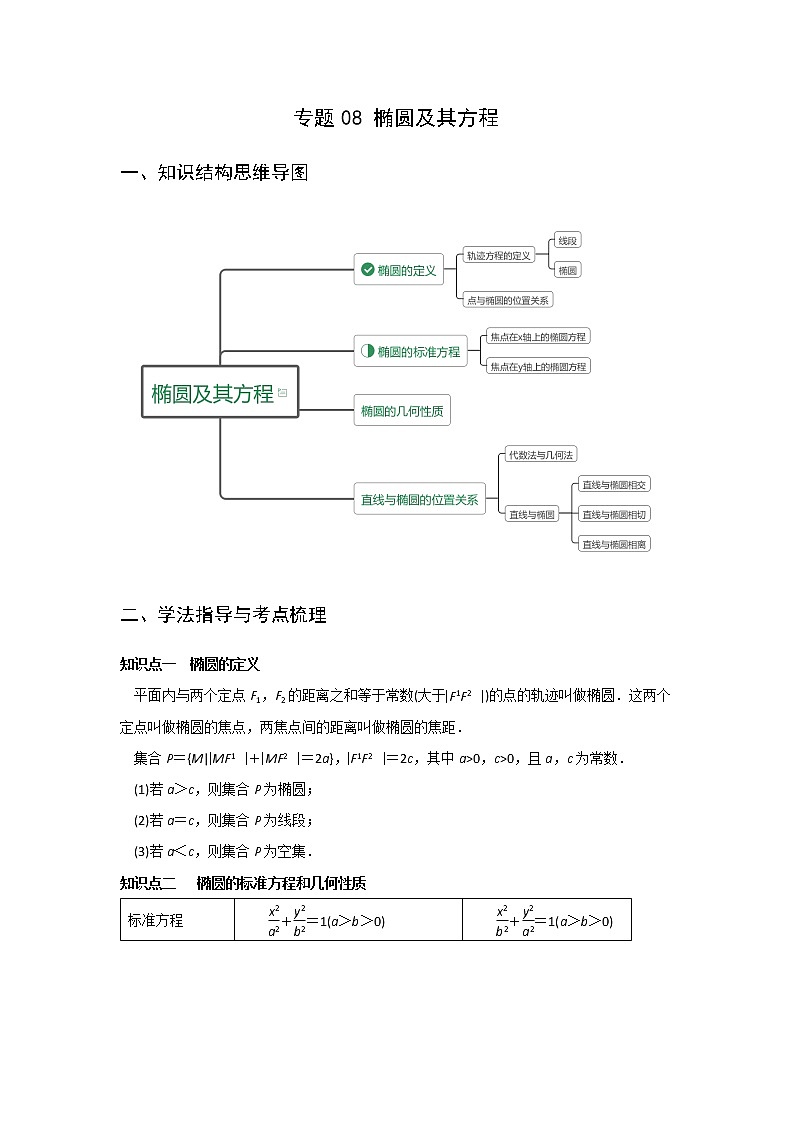
一、知识结构思维导图
二、学法指导与考点梳理
知识点一 椭圆的定义
平面内与两个定点F1,F2的距离之和等于常数(大于)的点的轨迹叫做椭圆.这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距.
集合P={M|+=2a},=2c,其中a>0,c>0,且a,c为常数.
(1)若a>c,则集合P为椭圆;
(2)若a=c,则集合P为线段;
(3)若a<c,则集合P为空集.
知识点二 椭圆的标准方程和几何性质
标准方程 | +=1(a>b>0) | +=1(a>b>0) | |
图形 | |||
性质
| 范围 | -a≤x≤a, -b≤y≤b | -b≤x≤b, -a≤y≤a |
对称性 | 对称轴:坐标轴,对称中心:(0,0) | ||
顶点 | A1(-a,0),A2(a,0), B1(0,-b),B2(0,b) | A1(0,-a),A2(0,a), B1(-b,0),B2(b,0) | |
轴 | 长轴A1A2的长为2a,短轴B1B2的长为2b | ||
焦距 | =2c | ||
离心率 | e=, e∈(0,1) | ||
a,b,c 的关系 | c2=a2-b2 | ||
【知识必备】
1.焦半径:椭圆上的点P(x0,y0)与左(下)焦点F1与右(上)焦点F2之间的线段的长度叫做椭圆的焦半径,分别记作r1=|PF1|,r2=|PF2|.
(1)+=1(a>b>0),r1=a+ex0,r2=a-ex0;
(2)+=1(a>b>0),r1=a+ey0,r2=a-ey0;
(3)焦半径中以长轴为端点的焦半径最大和最小(近日点与远日点).
2.焦点三角形:椭圆上的点P(x0,y0)与两焦点构成的△PF1F2叫做焦点三角形,∠F1PF2=θ,△PF1F2的面积为S,则在椭圆+=1(a>b>0)中
(1)当P为短轴端点时,θ最大.
(2)S=|PF1||PF2|·sin θ=b2tan =c|y0|,当|y0|=b时,即点P为短轴端点时,S取最大值,最大值为bc.
(3)焦点三角形的周长为2(a+c).
3.焦点弦(过焦点的弦):焦点弦中以通径(垂直于长轴的焦点弦)最短,弦长lmin=.
4.AB为椭圆+=1(a>b>0)的弦,A(x1,y1),B(x2,y2),弦中点M(x0,y0),则
(1)弦长l=|x1-x2|= |y1-y2|;
(2)直线AB的斜率kAB=-.
三、重难点题型突破
重难点01 椭圆的定义及其应用
例1、( 河南郑州外国语学校2019届模拟)如图所示,一圆形纸片的圆心为O,F是圆内一定点,M是圆周上一动点,把纸片折叠使M与F重合,然后抹平纸片,折痕为CD,设CD与OM交于点P,则点P的轨迹是( )
A.椭圆 B.双曲线
C.抛物线 D.圆
【变式训练1】对于方程,
(1)若该方程表示焦点在x轴上的椭圆,则实数m的取值范围为________________;
(2)若该方程表示焦点在y轴上的椭圆,则实数m的取值范围为________________;
(3)若该方程表示椭圆,则实数m的取值范围为________________.
重难点02 椭圆的标准方程
例2.(1)(辽宁省抚顺一中2019届期中)椭圆C的中心在原点,焦点在x轴上,离心率等于,且它的一个顶点为(0,2),则椭圆C的标准方程为( )
A.+=1 B.+=1 C.+=1 D.+=1
(2).(黑龙江省佳木斯一中2019届期末)设椭圆+=1(m>0,n>0)的右焦点为(2,0),离心率为,则此椭圆的方程为________.
【变式训练1】.(山东省淄博一中2019届模拟)中心为原点,一个焦点为F(0,5)的椭圆,截直线y=3x-2所得弦中点的横坐标为,则该椭圆方程为( )
A.+=1 B.+=1 C.+=1 D.+=1
【变式训练2】.(四川省眉山一中2019届模拟)已知椭圆+=1(a>b>0)的右焦点为F2(3,0),离心率为e.
(1)若e=,求椭圆的方程;
(2)设直线y=kx与椭圆相交于A,B两点,M,N分别为线段AF2,BF2的中点,若坐标原点O在以MN为直径的圆上,且<e≤,求k的取值范围.
重难点03 椭圆的几何性质
例3.(1)(湖南省株洲二中2019届期末)已知焦点在y轴上的椭圆 +=1的长轴长为8,则m=( )
A.4 B.8 C.16 D.18
(2).(湖南省张家界一中2019届期末)已知△ABC的顶点B,C在椭圆+y2=1上,顶点A是椭圆的一个焦点,且椭圆的另外一个焦点在BC边上,则△ABC的周长是( )
A.2 B.6 C.4 D.12
【变式训练1】.( 江苏省苏州一中2019届期中)已知椭圆+=1的离心率为,则k的值为( )
A.-21 B.21 C.-或21 D.或-21
【变式训练2】.(山西省朔州一中2019届期中)椭圆C:+=1(a>b>0)的左焦点为F,若F关于直线x+y=0的对称点A是椭圆C上的点,则椭圆C的离心率为( )
A. B. C. D.-1
重难点04 直线与椭圆的位置关系
例4.( 山东省菏泽一中2019届模拟)已知椭圆+=1(a>b>0)的左顶点和上顶点分别为A,B.左、右焦点分别是F1,F2,在线段AB上有且只有一个点P满足PF1⊥PF2,则椭圆的离心率的平方为( )
A. B.
C. D.
例5.(安徽省马鞍山二中2019届期中)已知椭圆C:+=1(a>b>0)的离心率为,焦距为2,过点D(1,0)且不过点E(2,1)的直线l与椭圆C交于A,B两点,直线AE与直线x=3交于点M.
(1)求椭圆C的方程;
(2)若AB垂直于x轴,求直线MB的斜率.
【变式训练1】.(宁夏石嘴山一中2019届模拟)已知椭圆C的两个顶点分别为A(-2,0),B(2,0),焦点在x轴上,离心率为.
(1)求椭圆C的方程;
(2)点D为x轴上一点,过D作x轴的垂线交椭圆C于不同的两点M,N,过D作AM的垂线交BN于点E.求证:△BDE与△BDN的面积之比为4∶5.
四、课堂定时训练(45分钟)
1.(河南省濮阳一中2019届期末)设椭圆+=1的焦点为F1,F2,点P在椭圆上,若△PF1F2是直角三角形,则△PF1F2的面积为( )
A.3 B.3或
C. D.6或3
2.(广东省佛山一中2019届模拟)焦点在x轴上的椭圆方程为+=1(a>b>0),短轴的一个端点和两个焦点相连构成一个三角形,该三角形内切圆的半径为,则椭圆的离心率为( )
A. B. C. D.
3.(广东省梅州一中2019届模拟)若点O和点F分别为椭圆+=1的中心和左焦点,点P为椭圆上的任意一点,则·的最大值为 ( )
A.2 B.3 C.6 D.8
4.(山东省威海一中2019届模拟)设椭圆C:+=1(a>b>0)的右焦点为F,椭圆C上的两点A,B关于原点对称,且满足·=0,|FB|≤|FA|≤2|FB|,则椭圆C的离心率的取值范围是( )
A. B.
C. D.
5.(浙江省衢州一中2019届期中)已知P为椭圆+=1上的一点,M,N分别为圆(x+3)2+y2=1和圆(x-3)2+y2=4上的点,则|PM|+|PN|的最小值为________.
6.设,分别是椭圆的左、右焦点,过的直线交椭圆于,两点,且,,则椭圆的离心率为( )
A. B. C. D.
7.已知,为椭圆的左,右焦点,为的短轴的一个端点,直线与的另一个交点为,若为等腰三角形,则( )
A. B. C. D.3
8.已知椭圆:,左、右焦点分别为,过的直线交椭圆于两点,若的最大值为5,则的值是( )
A.1 B. C. D.
9.嫦娥四号月球探测器于2018年12月8日搭载长征三号乙运载火箭在西昌卫星发射中心发射.12日下午4点43分左右,嫦娥四号顺利进入了以月球球心为一个焦点的椭圆形轨道,如图中轨道③所示,其近月点与月球表面距离为公里,远月点与月球表面距离为公里.已知月球的直径为公里,则该椭圆形轨道的离心率约为( )
A. B. C. D.
10.(椭圆与圆结合)如图,,分别是椭圆的左、右顶点,圆的半径为2,过点作圆的切线,切点为,在轴的上方交椭圆于点,则_______.








