

高中数学人教A版 (2019)选择性必修 第三册第七章 随机变量及其分布本章综合与测试达标测试
展开达标检测卷
随机变量及其分布(B)
注意事项:
1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.从混有张假钞票的张百元钞票中任意抽出张,将其中张放到验钞机上检验发现是假钞,则第张也是假钞的概率为( )
A.B.C.D.
2.某学校位同学组成的志愿者组织分别由李老师和张老师负责,每次献爱心活动均需该组织位同学参加.假设李老师和张老师分别将各自活动通知的信息独立,随机地发给位同学,且所发信息都能收到.则甲同学收到李老师或张老师所发活动通知的信息的概率为( )
A.B.C.D.
3.从装有除颜色外完全相同的个白球和个黑球的布袋中随机摸取一球,有放回的摸取次,设摸得白球数为,已知,则( )
A.B.C.D.
4.已知随机变量满足,,,,
若,则( )
A.,
B.,
C.,
D.,
5.国际象棋比赛中规定,胜方得分,负方得分,和棋得分.年浙江省青少年国际象棋公开赛中,某选手每场比赛得分的分布列如下:
且,则该选手进行一场比赛得分的期望一定不可能的是( )
A.B.C.D.
6.有件产品,其中件是次品,从中任取件,若表示取得次品的件数,
则( )
A.B.C.D.
7.设随机变量,满足:,,若,
则( )
A.B.C.D.
8.位于坐标原点的一个质点按下述规则移动:质点每次移动一个单位,移动的方向为向上或向右,并且向上、向右移动的概率都是,则质点移动六次后位于点的概率是( )
A.B.
C.D.
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分.
9.给出下列命题,其中正确的命题有( )
A.若,则是纯虚数
B.随机变量,若,则
C.公共汽车上有位乘客,沿途个车站,乘客下车的可能方式有种
D.回归方程为中,变量与具有正的线性相关关系
10.设离散型随机变量的分布列为
若离散型随机变量满足,则下列结果正确的有( )
A.B.
C.D.
11.甲箱中有个红球,个白球和个黑球,乙箱中有个红球,个白球和个黑球.先从甲箱中随机取出一球放入乙箱中,分别以,,表示由甲箱中取出的是红球,白球和黑球的事件;再从乙箱中随机取出一球,以表示由乙箱中取出的球是红球的事件,则下列结论正确的是( )
A.B.
C.事件与事件相互独立D.、、两两互斥
12.下列说法正确的是( )
A.在残差图中,残差点分布的水平带状区域越窄,说明模型的拟合效果越好
B.回归直线至少经过点,,,中的一个
C.若,,则
D.设随机变量,若,则
三、填空题:本大题共4小题,每小题5分.
13.从,,,,中任取个不同的数,事件“取到的个数之和为偶数”,事件“取到的个数均为偶数”,则______.
14.已知随机变量和,其中,且,若的分布列如下表,则的值为 .
15.现有件产品,其中件一等品,件二等品,从中随机选出件产品,其中一等品的件数记为随机变量,则的数学期望___________.
16.甲盒里装有个白球和个红球,乙盒里装有个白球和个红球,从甲、乙两个盒中各随机取个球放入原来为空的丙盒中,则从丙盒中取个球是白球的概率是______,丙盒中含有红球个数的期望是_________.
四、解答题:本大题共6个大题,共70分,解答应写出文字说明、证明过程或演算步骤.
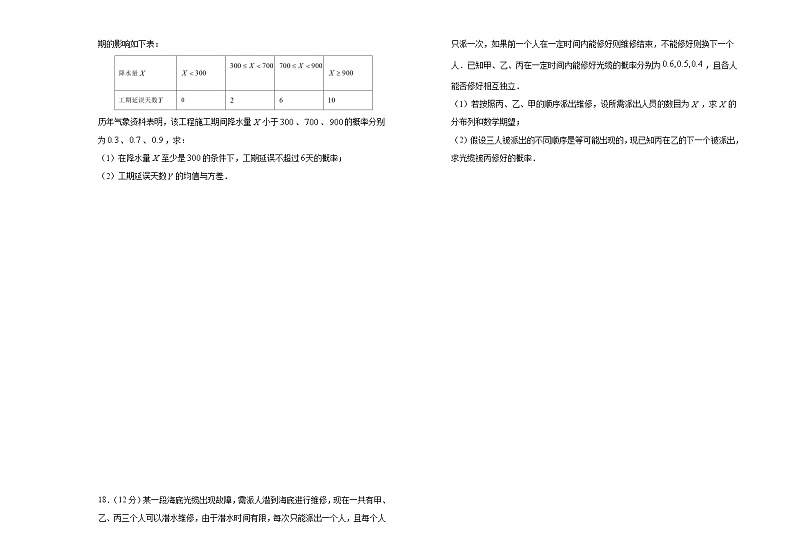
17.(10分)根据以往的经验,某工程施工期间的降水量(单位:)对工期的影响如下表:
历年气象资料表明,该工程施工期间降水量小于、、的概率分别为、、,求:
(1)在降水量至少是的条件下,工期延误不超过天的概率;
(2)工期延误天数的均值与方差.
18.(12分)某一段海底光缆出现故障,需派人潜到海底进行维修,现在一共有甲、乙、丙三个人可以潜水维修,由于潜水时间有限,每次只能派出一个人,且每个人只派一次,如果前一个人在一定时间内能修好则维修结束,不能修好则换下一个人.已知甲、乙、丙在一定时间内能修好光缆的概率分别为,且各人能否修好相互独立.
(1)若按照丙、乙、甲的顺序派出维修,设所需派出人员的数目为,求的分布列和数学期望;
(2)假设三人被派出的不同顺序是等可能出现的,现已知丙在乙的下一个被派出,求光缆被丙修好的概率.
19.(12分)三年前,中国有三分之二的城市面临“垃圾围城”的窘境.我国的垃圾处理多采用填埋的方式,占用上万亩土地,并且严重污染环境,垃圾分类把不易降解的物质分出来,减轻了土地的严重侵蚀,减少了土地流失.上海作为我国首个进行垃圾分类的城市,从年月开始实施至今,为了更好的回收和利用,每个小区都有规定时间投放垃圾,生活垃圾中有可以回收利用,分出可回收垃圾既环保,又节约资源.例如:回收利用1吨废纸可再造出吨好纸.现调查了上海市个小区年月的生活垃圾投放情况,其中在规定时间内投放垃圾的百分比和可回收物中废纸投放量如下表所示:
(1)从这个小区中任选个小区,求该小区年月在规定时间内投放垃圾的百分比不低于,且废纸投放量大于吨的概率;
(2)从这个小区中任选个小区,记为年月投放的废纸可再造好纸大于吨的小区个数,求的分布列及期望;
(3)若将频率视为概率,在上海市任选个小区,恰有个小区年月在规定时间内投放垃圾的百分比不低于,且废纸投放量大于吨的概率.
20.(12分)“一带一路”为世界经济增长开辟了新空间,为国际贸易投资搭建了新平台,为完善全球经济治理拓展了新实践.某企业为抓住机遇,计划在某地建立猕猴桃饮品基地,进行饮品,,的开发.
(1)在对三种饮品市场投放的前期调研中,对名试饮人员进行抽样调查,得到对三种饮品选择情况的条形图.若饮品的百件利润为元,饮品的百件利润为元,饮品的百件利润为元,请估计三种饮品的平均百件利润;
(2)为进一步提高企业利润,企业决定对饮品进行加工工艺的改进和饮品的研发.已知工艺改进成功的概率为,开发新饮品成功的概率为,且工艺改进与饮品研发相互独立;
①求工艺改进和新品研发恰有一项成功的概率;
②若工艺改进成功则可为企业获利万元,不成功则亏损万元,若饮品研发成功则获利万元,不成功则亏损万元,求该企业获利的数学期望.
21.(12分)工作人员需进入核电站完成某项具有高辐射危险的任务,每次只派一个人执行任务,且每个人只派一次.每人工作时间均不超过分钟,如果分钟内不能完成任务则撤出,再派下一个人;如果分钟内已完成任务则不再派人.现在一共只有甲乙丙三个人可派,他们各自能完成任务的概率分别为,,.假定各人能否完成任务相互独立.
(1)计划依次派甲乙丙执行任务,
①求能完成任务的概率;
②求派出人员数X的分布列和数学期望E(X).
(2)欲使完成任务的概率尽可能大,且所取需派出人员数X的数学期望尽可能小,你认为应该按什么次序派出甲乙丙?(直接写出答案即可)
22.(12分)《山东省高考改革试点方案》规定:从年秋季高中入学的新生开始,不分文理科;年开始,高考总成绩由语数外门统考科目和物理、化学等六门选考科目构成.将每门选考科目的考生原始成绩从高到低划分为、、、、、、、共个等级.参照正态分布原则,确定各等级人数所占比例分别为、、、、、、、.选考科目成绩计入考生总成绩时,将至等级内的考生原始成绩,依照等比例转换法则,分别转换到、、、、、、、八个分数区间,得到考生的等级成绩.某校高一年级共人,为给高一学生合理选科提供依据,对六个选考科目进行测试,其中物理考试原始成绩基本服从正态分布.
(1)求物理原始成绩在区间的人数;
(2)按高考改革方案,若从全省考生中随机抽取3人,记表示这3人中等级成绩在区间的人数,求的分布列和数学期望.
(附:若随机变量,则,,)
2020-2021学年选择性必修第三册第七单元
达标检测卷
随机变量及其分布(B)答 案
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.【答案】B
【解析】设“抽到的两张至少有一张是假钞”为事件,“抽到的两张都是假钞”为事件,
,,.
2.【答案】C
【解析】设甲同学收到李老师的信息为事件,收到张老师的信息为事件,
、相互独立,
,
则甲同学收到李老师或张老师所发活动通知的信息的概率为,故选C.
3.【答案】B
【解析】由题意知,,∴,解得,
∴,∴,
故选B.
4.【答案】C
【解析】依题意可知:
由于,不妨设.
故,,;,,,
故选C.
5.【答案】A
【解析】由随机变量的分布列可知,随机变量的数学期望为,
易知,,
∴,
即,当且仅当时,等号成立,
因此,该选手进行一场比赛得分的期望一定不可能的是,故选A.
6.【答案】B
【解析】根据题意,,
故选B.
7.【答案】A
【解析】由题意可得,
解得,
则,,本题选择A选项.
8.【答案】C
【解析】根据题意,易得位于坐标原点的质点移动六次后位于点,在移动过程中向上移动次向右移动次,
则其概率为,故选C.
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分.
9.【答案】BD
【解析】对于A,当时,是实数,故A错;
对于B,∵,∴,可得,
又∵,∴,故B正确;
对于C,公共汽车上有位乘客,沿途个车站,乘客下车的可能方式有种,故C错误;
对于D,回归方程为,由,可得变量与具有正的线性相关关系,故D正确,
综上所述正确的是BD,故选BD.
10.【答案】AC
【解析】由离散型随机变量的分布列的性质得:
,
则,
,
即,
因为离散型随机变量满足,
∴,
故结果正确的有AC,故选AC.
11.【答案】BD
【解析】因为每次取一球,所以,,是两两互斥的事件,故D正确;
因为,,,
所以,故B正确;
同理,,
所以,
故AC错误,
故选BD.
12.【答案】ACD
【解析】对于A,在残差图中,残差点比较均匀的分布在水平带状区域中,带状区域越窄,说明模型的拟合效果越好,选项正确;
对于B,线性回归直线不一定经过样本数据中的一个点,它是最能体现这组数据的变化趋势的直线,选项错误;
对于C,,选项正确;
对于D,随机变量,若,则,选项正确,
综上可得,正确的选项为ACD,故选ACD.
三、填空题:本大题共4小题,每小题5分.
13.【答案】
【解析】,,
由条件概率公式得,
故答案为.
14.【答案】
【解析】,,,
所以,且概率和,
解得.
15.【答案】
【解析】由题意可得:随机变量服从超几何分布:
,,,,
据此计算可得的数学期望.
16.【答案】,
【解析】由题意丙盒中白球的个数可能是,,,
因此所求概率为,
设丙盒中红球个数为,则可能是,,,
,,,
即的分布列为
所以.
故答案为;.
四、解答题:本大题共6个大题,共70分,解答应写出文字说明、证明过程或演算步骤.
17.【答案】(1);(2)均值为,方差为.
【解析】(1)由题意可得,
且工期延误不超过天的概率为
,
因此,在降水量至少是的条件下,工期延误不超过天的概率为.
(2)由题意可知,,
,
.
所以,随机变量的分布列如下表所示:
∴,
.
所以,工期延误天数的均值为,方差为.
18.【答案】(1)分布列见解析,期望为;(2).
【解析】(1)的可能取值为,,.
;;,
所以的分布列为
.
(2)由题意知,三人的顺序只可能有两种:“甲、乙、丙”或“乙、丙、甲”,且概率都为.
若为“甲、乙、丙”,则光缆被丙修好的概率为;
若为“乙、丙、甲”,则光缆被丙修好的概率为,
所以光缆被丙修好的概率为.
19.【答案】(1);(2)分布列见解析,;(3).
【解析】(1)记“该小区月份在规定时间内投放垃圾的百分比不低于,
且废纸投放量大于吨”为事件,只有、两个小区符合要求,
所以.
(2)因为回收利用吨废纸可再造出吨好纸,
所以月份投放的废纸可再造好纸大于4吨的小区有、两个小区,
的所有可能取值为,,.
,,.
所以的分布列为:
.
(3)设月份在规定时间内投放垃圾的百分比不低于,
且废纸投放量大于吨的小区个数为,则,
所以.
20.【答案】(1)元;(2)①;②.
【解析】(1)根据样本的条形图可得顾客选择饮品的频率为;
选择饮品的频率为;选择饮品的频率为,
则可以得到总体的百件利润平均值为元.
(2)①设饮品工艺改进成功为事件,新品研发成功为事件,
依题意可知事件与事件相互独立,
事件为工艺改进和新品研发恰有一项成功,
则.
②由题意知企业获利的取值为,10,120,230,
则,,
,.
故的分布列如下:
所以.
21.【答案】(1)①;②分布列见解析,;(2)依次派出丙甲乙.
【解析】(1)①设“计划依次派出甲乙丙,能完成任务”为事件.
因为甲乙丙各自能完成任务的概率分别为,,,
各人能否完成任务相互独立.
所以
或,
②依题意,的所有可能取值为,,.
,,.
所以的分布列为
故的期望.
(2)依次派出丙甲乙.
22.【答案】(1)人;(2)分布列见解析,.
【解析】(1)因为物理原始成绩,
所以
,
所以物理原始成绩在的人数为(人).
(2)由题意得,随机抽取人,其成绩在区间内的概率为,
所以随机抽取三人,则的所有可能取值为,,,,且,
所以,,
,.
所以的分布列为
所以数学期望.
人教版高中数学选择性必修第三册第七章 随机变量及其分布B卷提高训练(含解析): 这是一份人教版高中数学选择性必修第三册第七章 随机变量及其分布B卷提高训练(含解析),共12页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
高中数学人教A版 (2019)选择性必修 第三册7.4 二项分布与超几何分布课后测评: 这是一份高中数学人教A版 (2019)选择性必修 第三册7.4 二项分布与超几何分布课后测评,共15页。试卷主要包含了若x>0,5的展开式中,x3的系数为等内容,欢迎下载使用。
高中数学人教A版2019必修第二册 期末模拟卷 (含解析): 这是一份高中数学人教A版 (2019)必修 第二册全册综合当堂检测题,共29页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。













