高中数学人教B版 (2019)必修 第四册11.1.6 祖暅原理与几何体的体积优质课ppt课件

这是一份高中数学人教B版 (2019)必修 第四册11.1.6 祖暅原理与几何体的体积优质课ppt课件，共19页。PPT课件主要包含了水平截面面积，柱体的体积，锥体的体积，尝试与发现，补充练习，台体的体积，球的体积，因此每个零件的质量为，课堂小结等内容，欢迎下载使用。

一个几何体所占空间的大小称为这个几何体的体积，长方体的体积，圆柱的体积都等于底面积乘以高.那么能否求出其他几何体的体积呢？
同一摞书，当改变摆放书的形状时（如图所示），这摞书的总体积是否会改变？由此能得到有关体积的什么结论？
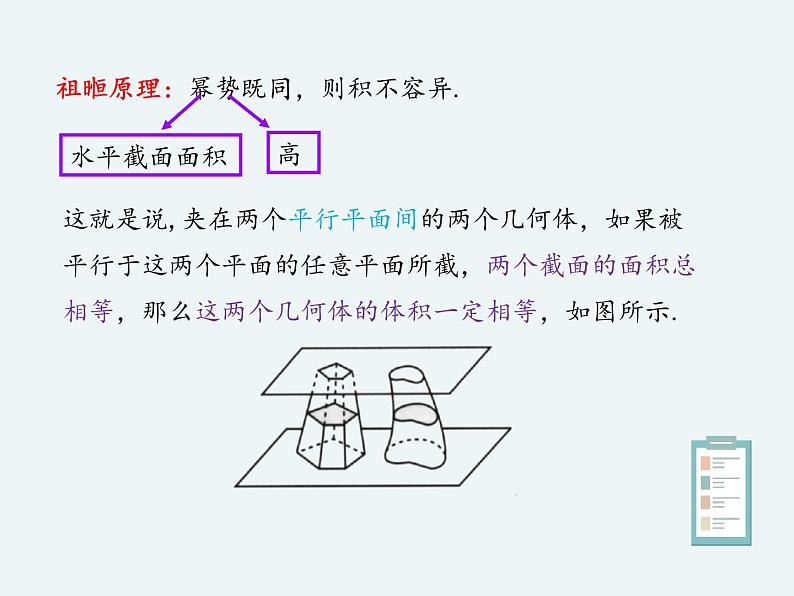
祖暅原理：幂势既同，则积不容异.
这就是说,夹在两个平行平面间的两个几何体，如果被平行于这两个平面的任意平面所截，两个截面的面积总相等，那么这两个几何体的体积一定相等，如图所示.
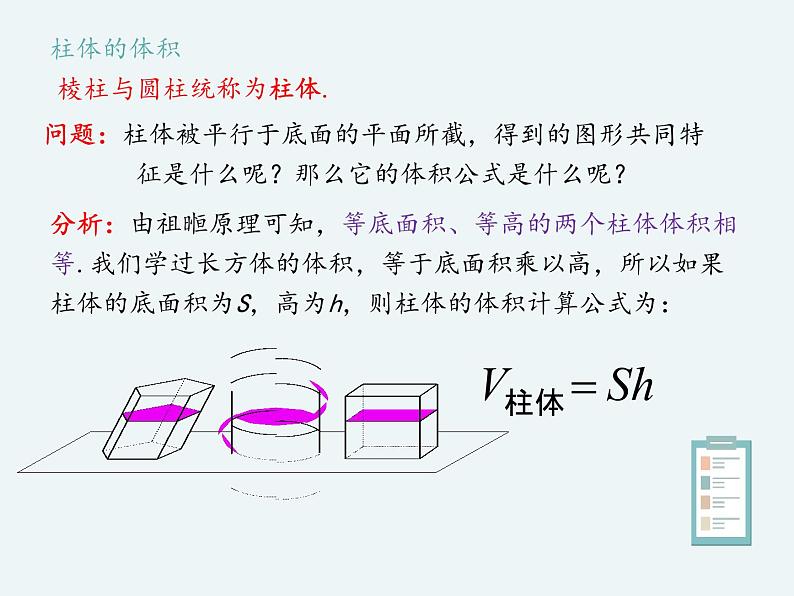
问题：柱体被平行于底面的平面所截，得到的图形共同特 征是什么呢？那么它的体积公式是什么呢？
分析：由祖暅原理可知，等底面积、等高的两个柱体体积相等.我们学过长方体的体积，等于底面积乘以高，所以如果柱体的底面积为S，高为h，则柱体的体积计算公式为：
棱柱与圆柱统称为柱体.
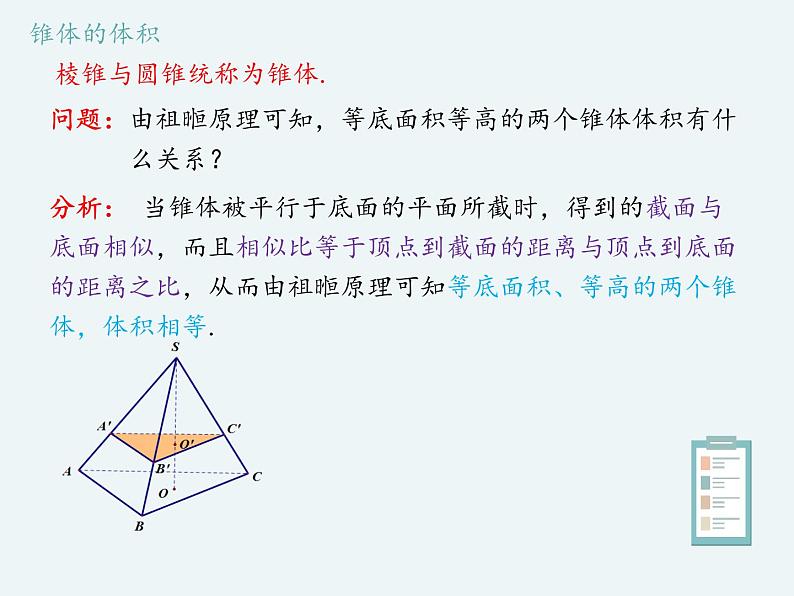
问题：由祖暅原理可知，等底面积等高的两个锥体体积有什 么关系？
分析： 当锥体被平行于底面的平面所截时，得到的截面与底面相似，而且相似比等于顶点到截面的距离与顶点到底面的距离之比，从而由祖暅原理可知等底面积、等高的两个锥体，体积相等.
棱锥与圆锥统称为锥体.
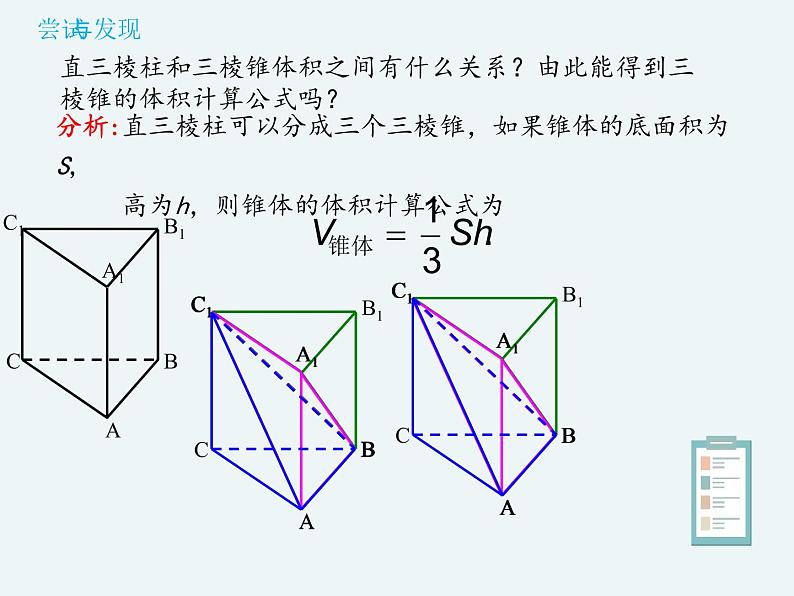
直三棱柱和三棱锥体积之间有什么关系？由此能得到三棱锥的体积计算公式吗？
分析:直三棱柱可以分成三个三棱锥，如果锥体的底面积为S, 高为h，则锥体的体积计算公式为
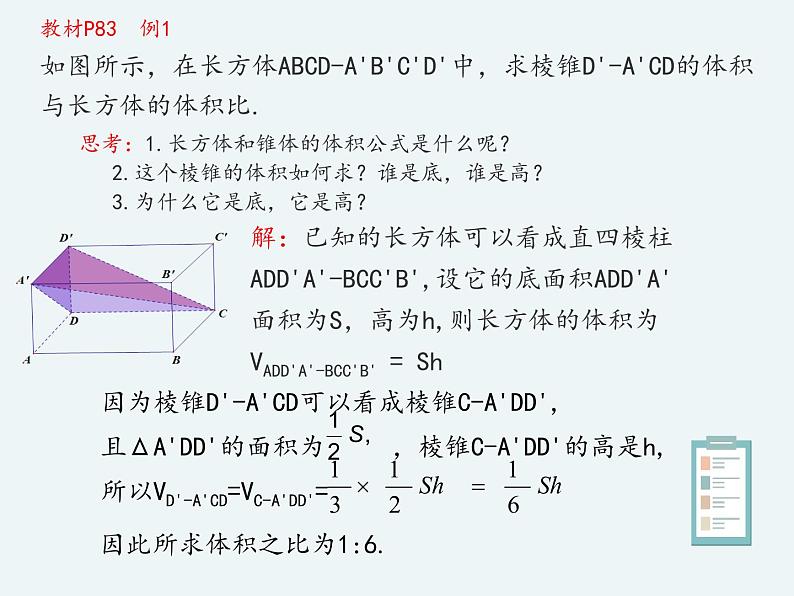
思考：1.长方体和锥体的体积公式是什么呢？ 2.这个棱锥的体积如何求？谁是底，谁是高？ 3.为什么它是底，它是高？
教材P83 例1如图所示，在长方体ABCD-A'B'C'D'中，求棱锥D'-A'CD的体积与长方体的体积比.
因此所求体积之比为1:6.
解：已知的长方体可以看成直四棱柱ADD'A'-BCC'B',设它的底面积ADD'A'面积为S，高为h,则长方体的体积为VADD'A'-BCC'B' = Sh
教材P87 练习B 3 《九章算术》中有如下问题：“今有委米依垣内角，下周八尺，高五尺.问积及为米几何.”其意思为：“在屋内墙角处堆放米（如图，米堆为一个圆锥的四分之一），米堆底部的弧长为8尺，米堆的高为5尺，问米堆的体积和堆放的米各为多少.”已知一斛米的体积约为1.62立方尺，圆周率为3，估算出堆放的米约有（ ）A.14斛 B.22斛 C.36斛 D.66斛
问题：我们学过柱体和锥体的体积公式，那么台体的体积可以通过我们已知的知识得到吗？
棱台与圆台统称为台体.
例2：已知四棱台上、下底面面积分别为S1,S2，而且高为h，求这个棱台的体积。
问题：柱体、锥体、台体它们的体积公式之间有怎样的联系呢？
其中S表示台体下底面积，S'表示台体上底面积。
空间几何体体积常用方法：（1）公式法（2）等积法（3）割补法
问题：（1）你能想出什么办法测出一个兵乓球的体积？ （2）如图所示是底面积和高都相等的两个几何体，右边是半球，左边是圆柱被挖去一个倒立的圆锥剩余的部分，用平行于半球与圆柱底面的平面去截这两个几何体，所得截面分别是什么形状？两个截面面积大小关系怎样？由此你能得到球的体积公式吗？
例3.如图，某铁制零件由一个正四棱柱和一个球组成，已知正四棱柱底面边长与球的直径均为1cm，正四棱柱的高为2cm，现有这种零件一盒共50kg，取铁的密度为7.8g/cm3，（1）估计有多少个这样的零件；（2）如果要给这盒零件的每个零件表面涂上一种特殊的材料，则需要能涂多少平方厘米的材料（球与接口处的面积不计，结果精确到1cm2）？
例3解:(1)每个零件的体积为
因此可估计出零件的个数为
(2)每个零件的表面积为
因此零件的表面积之和约为
即需要能涂33389cm2的材料
教材P87 练习题B 5 已知一个正三棱锥的四个顶点都在一个球的球面上，而且这个正三棱锥的所有棱长都为2，求这个球的体积
课后作业：教材87页A组第1、2、3、4题；89页习题11-1A第1、2、3、4题．教材87页B组第6题89页习题11-1A第16题