






人教B版 (2019)必修 第四册11.3.2 直线与平面平行优质ppt课件
展开问题:直线与平面的位置关系有哪些?如何用数学符号语言 来表示这些关系?
如图所示,如果将乒乓球台的台面抽象成平面a,将乒乓球网的上边缘抽象成直线l,则直线l与平面a具有怎样的位置关系?如果将乒乓球网的下边缘抽象成直线m,并把m看成平面a内的直线,则直线l与直线m具有怎样的位置关系?由此思考怎样才能证明直线与平面平行.
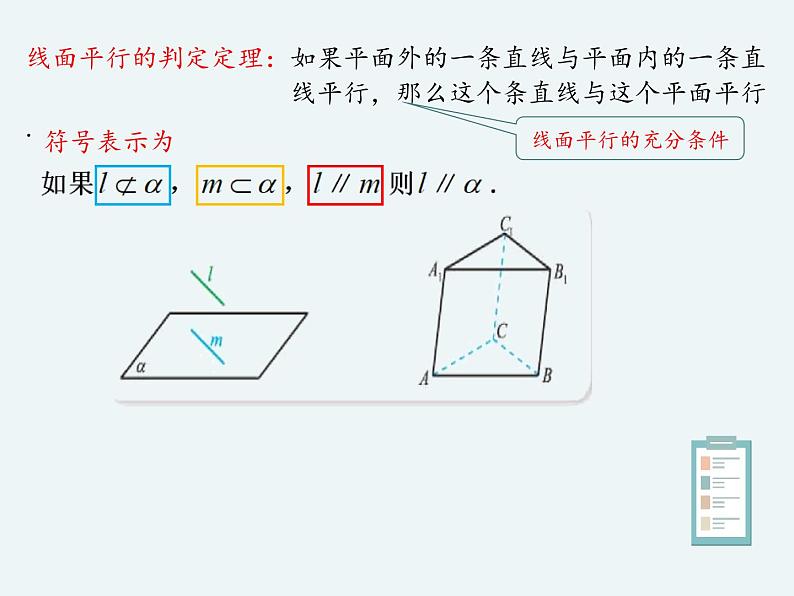
线面平行的判定定理:如果平面外的一条直线与平面内的一条直 线平行,那么这个条直线与这个平面平行.
例1 已知空间四边形ABCD中,E,F分别是边AB,AD的中点. 求证:EF ‖ 面BCD.
证明线面平行的方式:形成三角形中位线.
2.设a,β, γ是三个不同的平面,m,n是两条不同的直线,在命题“a∩β=m,n⊂γ,且 ,则m//n”中的横线处填入下列三组条件中的一组,使该命题为真命题.①a//γ,n⊂β;②m//γ, n//β; ③n//β, m⊂γ.可以填入的条件有 .
1.有下列命题①若直线 l 平行于平面α内的无数条直线,则直线l//α.②若直线a在平面α外,则a//α;③若直线a//b,b//α, 则a//α;④若直线a//b,b//α, 则a平行于平面α内的无数条直线.其中真命题的个数是( ).(A) 1 (B) 2 (C) 3 (D) 4
3.如图,三棱柱ABC-A1B1C1中,M,N分别是BC和A1B1的中点,E, F分别是B1C1和B1A的中点.求证: (1) EF//平面 ACC1A1; (2) 求证: MN//平面AA1C1.
提示: (1)连接AC1,证明EF//AC1即可; (2)取A1C1的中点,记为H.连接CH,证明四边形 NHCM是平行四边形即可。
判定定理证明线面平行的步骤
上面的第一步“找”是证题的关键,其常用方法有:①空间直线平行关系的传递性法;②三角形中位线法;③平行四边形法;
线面平行的性质定理:如果一条直线与一个平面平行,且经 过这条直线的平面与这个平面相交, 那么这条直线就与两平面的交线平行.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,AD=3,BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.求证:MN∥平面PAB.
如图,在四面体ABCD中,过棱AB的中点E作平行于AD,BC的平面,分别交四面体的棱BD,DC,CA于点F,G,H.求证:四边形EFGH是平行四边形.
注意:在利用直线与平面平行的性质定理时,不能直接说在平面内作一条直线与已知直线平行,一定要通过作平面来得到这条直线.
利用线面平行的性质定理证题的一般步骤
下列说法正确的是( )A.若直线a∥平面α,直线b∥平面α,则直线a∥直线bB.若直线a∥平面α,直线a与直线b相交,则直线b与平 面α相交C.若直线a∥平面α,直线a∥直线b,则直线b∥平面αD.若直线a∥平面α,则直线a与平面α内任意一条直线 都无公共点
D [A中直线a与直线b也可能异面、相交,所以不正确;B中,直线b也可能与平面α平行,所以不正确;C中,直线b也可能在平面α内,所以不正确;根据直线与平面平行的定义知D正确.]
4.判断下列命题的真假.(1) 如果直线a平行于直线b, 则a平行于经过b的任何一个平面;(2) 如果一条直线不在平面内,则这条直线就与这个平面平行;(3) 过直线外一点,可以作无数个平面与这条直线平行;(4)如果一条直线与一个平面平行,则它与该平面内的任何直线都平行.
教材P103 练习A 4
高中人教B版 (2019)第十一章 立体几何初步11.3 空间中的平行关系11.3.2 直线与平面平行课堂教学ppt课件: 这是一份高中人教B版 (2019)第十一章 立体几何初步11.3 空间中的平行关系11.3.2 直线与平面平行课堂教学ppt课件,文件包含人教B版高中数学必修第四册第11章1132直线与平面平行课件ppt、人教B版高中数学必修第四册第11章1132直线与平面平行学案doc、人教B版高中数学必修第四册课后素养落实17直线与平面平行含答案doc等3份课件配套教学资源,其中PPT共50页, 欢迎下载使用。
数学11.3.2 直线与平面平行评课ppt课件: 这是一份数学11.3.2 直线与平面平行评课ppt课件,共54页。PPT课件主要包含了有无数个,有且只有一个,l∥m,平面外,平面内,l⊄α,l⊂β,证明直线与平面平行等内容,欢迎下载使用。
必修 第四册第十一章 立体几何初步11.3 空间中的平行关系11.3.2 直线与平面平行集体备课ppt课件: 这是一份必修 第四册第十一章 立体几何初步11.3 空间中的平行关系11.3.2 直线与平面平行集体备课ppt课件,共20页。PPT课件主要包含了一引入,图形表示,答案D,当堂检测,答案A,答案C,答案B等内容,欢迎下载使用。














