
还剩22页未读,
继续阅读
2019-2020学年河北省石家庄十七中九年级(上)期中数学试卷
展开
2019-2020学年河北省石家庄十七中九年级(上)期中数学试卷
一.选择题(本大题共16小题,共42分.1-10小题各3分,11-16小题各2分,小题给出的四个选项中,只有一项是符合题目要求的)
1.(3分)sin30°的值为( )
A. B. C. D.
2.(3分)方程(x﹣2)2=0的根是( )
A.2 B.﹣2 C.0 D.无解
3.(3分)函数y=,当x>0时的图象为( )
A. B.
C. D.
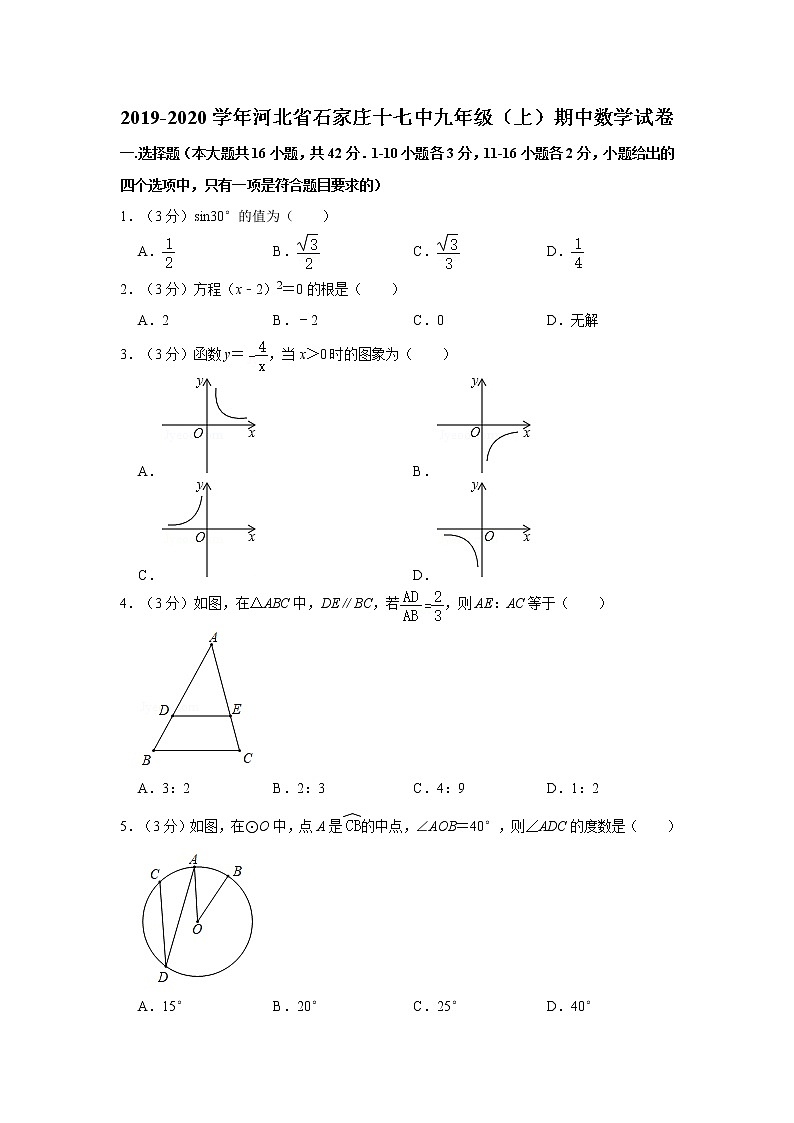
4.(3分)如图,在△ABC中,DE∥BC,若,则AE:AC等于( )
A.3:2 B.2:3 C.4:9 D.1:2
5.(3分)如图,在⊙O中,点A是的中点,∠AOB=40°,则∠ADC的度数是( )
A.15° B.20° C.25° D.40°
6.(3分)在同一平面内,过已知A、B、C三个点可以作圆的个数为( )
A.0个 B.1个 C.2个 D.0个或1个
7.(3分)某超市一月份的营业额为200万元,第一季度的营业额1000万元,如果平均每月增长率为x元,则由题意列方程应为( )
A.200(1+x)2=1000
B.200+200•2•x=1000
C.200+200•3•x=1000
D.200[1+(1+x)+(1+x)2]=1000
8.(3分)如图,在平面直角坐标系中,以原点O为位似中心,将△ABO扩大到原来的2倍,得到对应的△A′B′O.若点B的坐标是(﹣2,1),则点B′的坐标是( )
A.(4,﹣2) B.(﹣4,2) C.(2,﹣4) D.(﹣2,4)
9.(3分)a,b是实数,点A(4,a)、B(5,b)在反比例函数y=的图象上,则( )
A.a<b<0 B.b<a<0 C.a<0<b D.b<0<a
10.(3分)若⊙P的半径为5,圆心P的坐标为(﹣3,4),则平面直角坐标系的原点O与⊙P的位置关系是( )
A.在⊙P内 B.在⊙P上 C.在⊙P外 D.无法确定
11.(2分)若关于x的方程x2﹣x+sina=0有两个相等的实数根,则锐角a为( )
A.75° B.60° C.45° D.30°
12.(2分)已知圆锥的底面半径为5cm,母线长为13cm,则这个圆锥的侧面积是( )
A.60πcm2 B.65πcm2 C.120πcm2 D.130πcm2
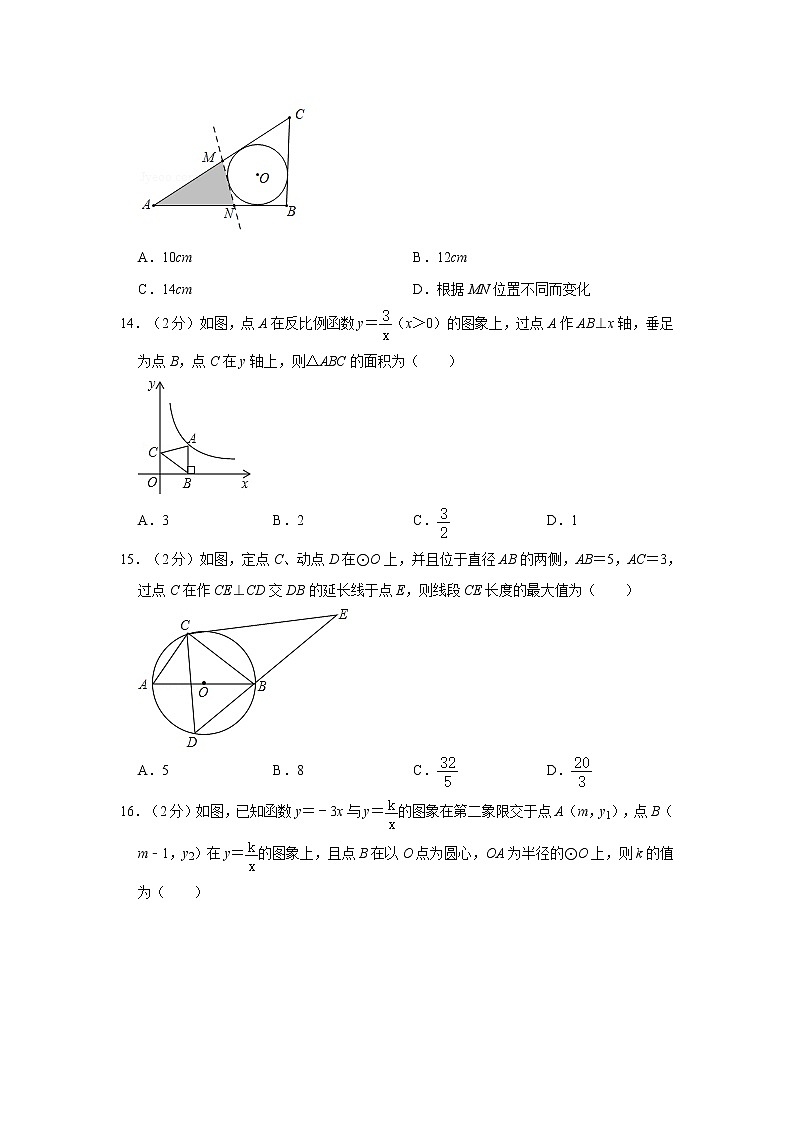
13.(2分)如图,三角形纸片ABC的周长为22cm,BC=6cm,⊙O是△ABC的内切圆,玲玲用剪刀在⊙O的左侧沿着与⊙O相切的任意一条直线MN剪下一个△AMN,则△AMN的周长是( )
A.10cm B.12cm
C.14cm D.根据MN位置不同而变化
14.(2分)如图,点A在反比例函数y=(x>0)的图象上,过点A作AB⊥x轴,垂足为点B,点C在y轴上,则△ABC的面积为( )
A.3 B.2 C. D.1
15.(2分)如图,定点C、动点D在⊙O上,并且位于直径AB的两侧,AB=5,AC=3,过点C在作CE⊥CD交DB的延长线于点E,则线段CE长度的最大值为( )
A.5 B.8 C. D.
16.(2分)如图,已知函数y=﹣3x与y=的图象在第二象限交于点A(m,y1),点B(m﹣1,y2)在y=的图象上,且点B在以O点为圆心,OA为半径的⊙O上,则k的值为( )
A.﹣ B.﹣1 C.﹣ D.﹣2
二.填空题(本大题共3小题,共11分.17小题3分;18-19小题各有2个空,每个空2分.把答案写在答题卡相应题号中的横线上)
17.(3分)如图,某游乐场一山顶滑梯的高为h,滑梯的坡角为α,那么滑梯长l为 .
18.(3分)已知正六边形的边长为2,则它的内切圆的半径是 ,扇形AOB的面积 .
19.(4分)如图,在矩形ABCD中,AB=4,AD=6,E是AB边的中点,F是线段BC上的动点,将△EBF沿EF所在直线折叠得到△EB′F,连接ED,则DE的长度是 ,B′D的最小值是 .
三.解答题(本大题共7小题,共67分.解答应写出文字说明、证明过程或演算步骤)
20.(8分)(1)解方程:x(x﹣1)=2;
(2)(1﹣sin45°)0﹣tan60°+.
21.(9分)如图,在Rt△AOB中,∠ABO=90°,OB=4,AB=8,且反比例函数y=在第一象限内的图象分别交OA,AB于点C和点D,连结OD,△BOD的面积是4.
(1)求反比例函数解析式;
(2)将△AOB沿x轴向左运动,运动速度是每秒钟3个单位长度,求△AOB与反比例函数图象没有交点时,运动时间t的取值范围.
22.(10分)已知,如图,==,那么△ABD与△BCE相似吗?为什么?
23.(9分)如图,学校打算用16m的篱笆围成一个长方形的生物园饲养小兔,生物园的一面靠墙(如图),面积是30m2.求生物园的长和宽.
24.(10分)为了计算湖中小岛上凉亭P到岸边公路l的距离,某数学兴趣小组在公路l上的点A处,测得凉亭P在北偏东60°的方向上;从A处向正东方向行走200米,到达公路l上的点B处,再次测得凉亭P在北偏东45°的方向上,如图所示.求凉亭P到公路l的距离.(结果保留整数,参考数据:≈1.414,≈1.732)
25.(10分)如图,PA是⊙O的切线,切点为A,AC是⊙O的直径,连接OP交⊙O于E.过A点作AB⊥PO于点D,交⊙O于B,连接BC,PB.
(1)求证:PB是⊙O的切线;
(2)求证:E为△PAB的内心;
(3)若cos∠PAB=,BC=1,求PO的长.
26.(12分)如图1,平行四边形ABCD中,AB⊥AC,AB=6,AD=10,点P在边AD上运动,以P为圆心,PA为半径的⊙P与对角线AC交于A,E两点.
(1)线段AC的长度是 .
(2)如图2,当⊙P与边CD相切于点F时,求AP的长;
(3)不难发现,当⊙P与边CD相切时,⊙P与平行四边形ABCD的边有三个公共点,随着AP的变化,⊙P与平行四边形ABCD的边的公共点的个数也在变化,若公共点的个数为4,直接写出相对应的AP的值的取值范围 .
2019-2020学年河北省石家庄十七中九年级(上)期中数学试卷
参考答案与试题解析
一.选择题(本大题共16小题,共42分.1-10小题各3分,11-16小题各2分,小题给出的四个选项中,只有一项是符合题目要求的)
1.(3分)sin30°的值为( )
A. B. C. D.
【分析】根据特殊角三角函数值,可得答案.
【解答】解:sin30°=,
故选:A.
【点评】本题考查了特殊角三角函数值,熟记特殊角三角函数值是解题关键.
2.(3分)方程(x﹣2)2=0的根是( )
A.2 B.﹣2 C.0 D.无解
【分析】根据直接开方法即可求出答案
【解答】解:∵(x﹣2)2=0,
∴x1=x2=2,
故选:A.
【点评】本题考查一元二次方程,解题的关键是熟练运用一元二次方程的解法,本题属于基础题型.
3.(3分)函数y=,当x>0时的图象为( )
A. B.
C. D.
【分析】根据反比例函数的比例系数可得图象在二或四象限,根据自变量的取值可得图象的准确象限.
【解答】解:∵反比例函数的比例系数为﹣4,
∴反比例函数的图象在第二、四象限,
∵x>0,
∴图象在第四象限,
故选:B.
【点评】考查反比例函数的性质;用到的知识点为:反比例函数的比例系数为负数,图象在二四象限;第四象限点的坐标的符号为(+,﹣).
4.(3分)如图,在△ABC中,DE∥BC,若,则AE:AC等于( )
A.3:2 B.2:3 C.4:9 D.1:2
【分析】由DE∥CB,根据平行线分线段成比例定理,可求得AE、AC的比例关系.
【解答】解:∵DE∥BC,AD:DB=2:3,
∴AE:AC=2:3.
故选:B.
【点评】此题主要考查了平行线分线段成比例定理,根据已知得出AE与EC的关系是解题关键.
5.(3分)如图,在⊙O中,点A是的中点,∠AOB=40°,则∠ADC的度数是( )
A.15° B.20° C.25° D.40°
【分析】直接利用圆周角求解.
【解答】解:∵点A是的中点,
∴=,
∴∠ADC=∠AOB=×40°=20°.
故选:B.
【点评】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
6.(3分)在同一平面内,过已知A、B、C三个点可以作圆的个数为( )
A.0个 B.1个 C.2个 D.0个或1个
【分析】分两种情况讨论:①A、B、C三个点共线,不能做圆;②A、B、C三个点不在同一条直线上,有且只有一个圆.
【解答】解:当A、B、C三个点共线,过A、B、C三个点不能作圆;
当A、B、C不在同一条直线上,过A、B、C三个点的圆有且只有一个,即三角形的外接圆;
故选:D.
【点评】本题考查了确定圆的条件,注:过三点作圆,分两种情况:①三点共线;②三点不共线.
7.(3分)某超市一月份的营业额为200万元,第一季度的营业额1000万元,如果平均每月增长率为x元,则由题意列方程应为( )
A.200(1+x)2=1000
B.200+200•2•x=1000
C.200+200•3•x=1000
D.200[1+(1+x)+(1+x)2]=1000
【分析】根据题意可以列出相应的方程,本题得以解决.
【解答】解:由题意可得,
200+200(1+x)+200(1+x)2=1000,
200[1+(1+x)+(1+x)2]=1000,
故选:D.
【点评】本题考查由实际问题抽象出一元二次方程,解题的关键是明确题意,列出相应的方程.
8.(3分)如图,在平面直角坐标系中,以原点O为位似中心,将△ABO扩大到原来的2倍,得到对应的△A′B′O.若点B的坐标是(﹣2,1),则点B′的坐标是( )
A.(4,﹣2) B.(﹣4,2) C.(2,﹣4) D.(﹣2,4)
【分析】根据以原点O为位似中心,将△ABO扩大到原来的2倍,即可得出对应点的坐标应乘以﹣2,即可得出点B′的坐标.
【解答】解:根据以原点O为位似中心,图形的坐标特点得出,对应点的坐标应乘以﹣2,
故点B的坐标是(﹣2,1),则点B′的坐标是(4,﹣2),
故选:A.
【点评】此题主要考查了关于原点对称的位似图形的性质,得出对应点的坐标乘以k或﹣k是解题关键.
9.(3分)a,b是实数,点A(4,a)、B(5,b)在反比例函数y=的图象上,则( )
A.a<b<0 B.b<a<0 C.a<0<b D.b<0<a
【分析】由k=﹣3<0,可得到图象位于二、四象限,y随x的增大而增大,再由A(4,a)、B(5,b)两点横坐标的大小判断出a、b,再由图象的位置进而判断出a、b、0,之间的关系.
【解答】解:∵k=﹣3<0,
∴图象位于二、四象限,在每个象限内,y随x的增大而增大,
∴点A(4,a)、B(5,b)在第四象限内图象上的两点,
∴a<b<0,
故选:A.
【点评】考查反比例函数的图象和性质,掌握反比例函数的图象和性质是正确判断的前提,利用图象法则会更直观.
10.(3分)若⊙P的半径为5,圆心P的坐标为(﹣3,4),则平面直角坐标系的原点O与⊙P的位置关系是( )
A.在⊙P内 B.在⊙P上 C.在⊙P外 D.无法确定
【分析】由勾股定理等性质算出点与圆心的距离d,则d>r时,点在圆外;当d=r时,点在圆上;当d<r时,点在圆内.
【解答】解:由勾股定理,得
OP==5,
d=r=5,
原点O在⊙P上.
故选:B.
【点评】本题考查了对点与圆的位置关系的判断.关键要记住若半径为r,点到圆心的距离为d,则有:当d>r时,点在圆外;当d=r时,点在圆上,当d<r时,点在圆内.
11.(2分)若关于x的方程x2﹣x+sina=0有两个相等的实数根,则锐角a为( )
A.75° B.60° C.45° D.30°
【分析】根据判别式的意义得到△=(﹣)2﹣4sinα=0,从而可求出α的正弦值,然后根据特殊角的三角函数值确定α的度数.
【解答】解:根据题意得△=(﹣)2﹣4sinα=0,
解得sinα=,
所以锐角α=30°.
故选:D.
【点评】本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2﹣4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.也考查了特殊角的三角函数值.
12.(2分)已知圆锥的底面半径为5cm,母线长为13cm,则这个圆锥的侧面积是( )
A.60πcm2 B.65πcm2 C.120πcm2 D.130πcm2
【分析】利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形面积公式计算.
【解答】解:这个圆锥的侧面积=×2π×5×13=65π(cm2).
故选:B.
【点评】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.
13.(2分)如图,三角形纸片ABC的周长为22cm,BC=6cm,⊙O是△ABC的内切圆,玲玲用剪刀在⊙O的左侧沿着与⊙O相切的任意一条直线MN剪下一个△AMN,则△AMN的周长是( )
A.10cm B.12cm
C.14cm D.根据MN位置不同而变化
【分析】设E,F,G,H分别是直线AC,AB,MN,BC与⊙O的切点.根据△AMN的周长=AM+AN+MG+NF=AM+ME+AN+NF=AE+AF,想办法求出AE+AF即可解决问题.
【解答】解:设E,F,G,H分别是直线AC,AB,MN,BC与⊙O的切点.
由切线长定理可知:CE=CH,BH=BF.ME=MG,NG=NF,
∵AC+AB+BC=22cm,BC=6cm,
∴AC+AB=16cm,AE+AF=10cm,
∴△AMN的周长=AM+AN+MG+NF=AM+ME+AN+NF=AE+AF=10cm,
故选:A.
【点评】本题考查三角形的内切圆与内心,切线长定理等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
14.(2分)如图,点A在反比例函数y=(x>0)的图象上,过点A作AB⊥x轴,垂足为点B,点C在y轴上,则△ABC的面积为( )
A.3 B.2 C. D.1
【分析】连结OA,如图,利用三角形面积公式得到S△OAB=S△CAB,再根据反比例函数的比例系数k的几何意义得到S△OAB=|k|,便可求得结果.
【解答】解:连结OA,如图,
∵AB⊥x轴,
∴OC∥AB,
∴S△OAB=S△CAB,
而S△OAB=|k|=,
∴S△CAB=,
故选:C.
【点评】本题考查了反比例函数的比例系数k的几何意义:在反比例函数y=图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.
15.(2分)如图,定点C、动点D在⊙O上,并且位于直径AB的两侧,AB=5,AC=3,过点C在作CE⊥CD交DB的延长线于点E,则线段CE长度的最大值为( )
A.5 B.8 C. D.
【分析】当CD是直径时,CE最长,由AB是直径,得到∠ACB=90°,利用勾股定理得出BC的长度,又因为∠A=∠D,∠ABC=∠ACE=90°,推出△ABC∽△DCE,根据相似三角形的性质列方程求解.
【解答】解:当CD是直径时,CE最长,
∵AB是直径,
∴∠ACB=90°,
∴BC=,
∵∠A=∠D,∠ABC=∠ACE=90°,
∴△ABC∽△DCE,
∴,
即,
∴CE=,
故选:D.
【点评】本题考查了相似三角形的判定和性质,圆周角定理,解直角三角形,勾股定理的应用,确定CE什么时候取最大值是解题的关键.
16.(2分)如图,已知函数y=﹣3x与y=的图象在第二象限交于点A(m,y1),点B(m﹣1,y2)在y=的图象上,且点B在以O点为圆心,OA为半径的⊙O上,则k的值为( )
A.﹣ B.﹣1 C.﹣ D.﹣2
【分析】由题意A(m,﹣3m),因为⊙O与反比例函数y=都是关于直线y=﹣x对称,推出A与B关于直线y=﹣x对称,推出B(3m,﹣m),可得3m=m﹣1,求出m即可解决问题;
【解答】解:∵函数y=﹣3x与y=的图象在第二象限交于点A(m,y1),
∴点A(m,﹣3m)
∵∵⊙O与反比例函数y=都是关于直线y=﹣x对称,
∴A与B关于直线y=﹣x对称,
∴B(3m,﹣m),
∴3m=m﹣1,
∴m=﹣
∴点A(﹣,)
∴k=﹣×=﹣
故选:A.
【点评】本题考查反比例函数与一次函数的交点问题,解题的关键是灵活运用所学知识解决问题,本题的突破点是发现A,B关于直线y=﹣x对称.
二.填空题(本大题共3小题,共11分.17小题3分;18-19小题各有2个空,每个空2分.把答案写在答题卡相应题号中的横线上)
17.(3分)如图,某游乐场一山顶滑梯的高为h,滑梯的坡角为α,那么滑梯长l为 .
【分析】根据三角函数的定义即可求解.
【解答】解:∵sina=,
∴l=.
故答案为:.
【点评】本题考查了解直角三角形﹣坡度与坡角,三角函数的定义,理解定义是关键.
18.(3分)已知正六边形的边长为2,则它的内切圆的半径是 ,扇形AOB的面积 .
【分析】根据题意画出图形,利用正六边形中的等边三角形的性质求解即可.
【解答】解:如图,连接OA、OB,OG;
∵六边形ABCDEF是边长为2的正六边形,
∴△OAB是等边三角形,
∴OA=AB=2,
∴OG=OA•sin60°=2×=,
∴边长为2的正六边形的内切圆的半径;
外接圆半径为2,扇形AOB的面积=,
故答案为,.
【点评】本题考查学生对正多边形的概念掌握和计算的能力.解答这类题往往一些学生因对正多边形的基本知识不明确,将多边形的半径与内切圆的半径相混淆而造成错误计算,记住基本概念是解题的关键,属于中考常考题型.
19.(4分)如图,在矩形ABCD中,AB=4,AD=6,E是AB边的中点,F是线段BC上的动点,将△EBF沿EF所在直线折叠得到△EB′F,连接ED,则DE的长度是 2 ,B′D的最小值是 2﹣2 .
【分析】根据翻折变换可得EB′=EB,∠EB′F=∠B=90°,E是AB边的中点,根据勾股定理可求解.
【解答】解:∵四边形ABCD是矩形,
∴∠A=∠B=90°,AD=6,AB=4,
∵E是AB边的中点,
∴AE=BE==2,
∴根据勾股定理,得
DE===2.
由折叠可知:
点B折叠后对应点B‘应是在以E为圆心,BE为半径的圆上运动,
所以DB'最小值应为B'在DE上时最小.
∴DB′的最小值为DE﹣BE=2﹣2.
故答案为2、2﹣2.
【点评】本题考查了翻折变换、矩形的性质,解决本题的关键是熟练运用翻折的性质.
三.解答题(本大题共7小题,共67分.解答应写出文字说明、证明过程或演算步骤)
20.(8分)(1)解方程:x(x﹣1)=2;
(2)(1﹣sin45°)0﹣tan60°+.
【分析】(1)整理后分解因式,即可得出两个一元一次方程,求出方程的解即可;
(2)先根据零指数幂,特殊角的三角函数值,算术平方根求出每一部分的值,再算加减即可.
【解答】解:(1)x(x﹣1)=2,
x2﹣x﹣2=0,
(x﹣2)(x+1)=0,
x﹣2=0,x+1=0,
x1=2,x2=﹣1;
(2)原式=1﹣+2
=3﹣.
【点评】本题考查了解一元二次方程,特殊角的三角函数值,零指数幂,算术平方根等知识点,能把一元二次方程转化成一元方程是解(1)的关键,能求出每一部分的值是解(2)的关键.
21.(9分)如图,在Rt△AOB中,∠ABO=90°,OB=4,AB=8,且反比例函数y=在第一象限内的图象分别交OA,AB于点C和点D,连结OD,△BOD的面积是4.
(1)求反比例函数解析式;
(2)将△AOB沿x轴向左运动,运动速度是每秒钟3个单位长度,求△AOB与反比例函数图象没有交点时,运动时间t的取值范围.
【分析】(1)根据反比例函数y=(k≠0)系数k的几何意义得到S△BOD=k=4,求出k即可确定反比例函数解析式;
(2)由反比例函数的性质即可判断A点在反比例函数的图象时t的值,即可得到t的取值范围.
【解答】解:(1)∵S△BOD=k,
∴k=4,解得k=8,
∴反比例函数解析式为y=;
(2)当A点移到反比例函数图象上,
∵AB=8,
∴A的纵坐标为8,
代入y=求得x=1,
此时A移到的距离为4﹣1=3,
∵3÷3=1,
∴t>1.
【点评】本题考查了反比例函数y=(k≠0)系数k的几何意义:从反比例函数y=kx(k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|.
22.(10分)已知,如图,==,那么△ABD与△BCE相似吗?为什么?
【分析】先根据三组对应边的比相等的两个三角形相似判断△ABC∽△DBE,得到∠ABC=∠DBE,则∠ABD=∠CBE,再利用比例性质由=得到=,于是根据两组对应边的比相等且夹角对应相等的两个三角形相似可判断△ABD∽△CBE.
【解答】解:∵==,
∴△ABC∽△DBE,
∴∠ABC=∠DBE,
∴∠ABC﹣∠DBC=∠DBE﹣∠DBC,
即∠ABD=∠CBE,
∵=,
∴=,
∴△ABD∽△CBE.
【点评】本题考查了相似三角形的判定:三组对应边的比相等的两个三角形相似;两组对应边的比相等且夹角对应相等的两个三角形相似.
23.(9分)如图,学校打算用16m的篱笆围成一个长方形的生物园饲养小兔,生物园的一面靠墙(如图),面积是30m2.求生物园的长和宽.
【分析】可设宽为x m,则长为(16﹣2x)m,根据等量关系:面积是30m2.列出方程求解即可.
【解答】解:设宽为x m,则长为(16﹣2x)m.
由题意,得 x•(16﹣2x)=30,
解得 x1=3,x2=5.
当x=3时,16﹣2×3=10,
当x=5时,16﹣2×5=6.
答:围成矩形的长为10 m、宽为3 m,或长为6 m、宽为5m.
【点评】考查了一元二次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.
24.(10分)为了计算湖中小岛上凉亭P到岸边公路l的距离,某数学兴趣小组在公路l上的点A处,测得凉亭P在北偏东60°的方向上;从A处向正东方向行走200米,到达公路l上的点B处,再次测得凉亭P在北偏东45°的方向上,如图所示.求凉亭P到公路l的距离.(结果保留整数,参考数据:≈1.414,≈1.732)
【分析】作PD⊥AB于D,构造出Rt△APD与Rt△BPD,根据AB的长度.利用特殊角的三角函数值求解.
【解答】解:作PD⊥AB于D.
设BD=x,则AD=x+200.
∵∠EAP=60°,
∴∠PAB=90°﹣60°=30°.
在Rt△BPD中,
∵∠FBP=45°,
∴∠PBD=∠BPD=45°,
∴PD=DB=x.
在Rt△APD中,
∵∠PAB=30°,
∴PD=tan30°•AD,
即DB=PD=tan30°•AD,
可得:x=(200+x),
解得:x≈273.2,
∴PD≈273.
答:凉亭P到公路l的距离为273m.
【点评】此题考查的是直角三角形的性质,解答此题的关键是构造出两个特殊角度的直角三角形,再利用特殊角的三角函数值解答.
25.(10分)如图,PA是⊙O的切线,切点为A,AC是⊙O的直径,连接OP交⊙O于E.过A点作AB⊥PO于点D,交⊙O于B,连接BC,PB.
(1)求证:PB是⊙O的切线;
(2)求证:E为△PAB的内心;
(3)若cos∠PAB=,BC=1,求PO的长.
【分析】(1)连结OB,根据圆周角定理得到∠ABC=90°,证明△AOP≌△BOP,得到∠OBP=∠OAP,根据切线的判定定理证明;
(2)连结AE,根据切线的性质定理得到∠PAE+∠OAE=90°,证明EA平分∠PAD,根据三角形的内心的概念证明即可;
(3)根据余弦的定义求出OA,证明△PAO∽△ABC,根据相似三角形的性质列出比例式,计算即可.
【解答】(1)证明:连结OB,
∵AC为⊙O的直径,
∴∠ABC=90°,
∵AB⊥PO,
∴PO∥BC
∴∠AOP=∠C,∠POB=∠OBC,
OB=OC,
∴∠OBC=∠C,
∴∠AOP=∠POB,
在△AOP和△BOP中,
,
∴△AOP≌△BOP(SAS),
∴∠OBP=∠OAP,
∵PA为⊙O的切线,
∴∠OAP=90°,
∴∠OBP=90°,
∴PB是⊙O的切线;
(2)证明:连结AE,
∵PA为⊙O的切线,
∴∠PAE+∠OAE=90°,
∵AD⊥ED,
∴∠EAD+∠AED=90°,
∵OE=OA,
∴∠OAE=∠AED,
∴∠PAE=∠DAE,即EA平分∠PAD,
∵PA、PB为⊙O的切线,
∴PD平分∠APB
∴E为△PAB的内心;
(3)解:∵∠PAB+∠BAC=90°,∠C+∠BAC=90°,
∴∠PAB=∠C,
∴cos∠C=cos∠PAB=,
在Rt△ABC中,cos∠C===,
∴AC=,AO=,
∵△PAO∽△ABC,
∴,
∴PO===5.
【点评】本题考查的是三角形的内切圆和内心、相似三角形的判定和性质、切线的判定,掌握切线的判定定理、相似三角形的判定定理和性质定理是解题的关键.
26.(12分)如图1,平行四边形ABCD中,AB⊥AC,AB=6,AD=10,点P在边AD上运动,以P为圆心,PA为半径的⊙P与对角线AC交于A,E两点.
(1)线段AC的长度是 8 .
(2)如图2,当⊙P与边CD相切于点F时,求AP的长;
(3)不难发现,当⊙P与边CD相切时,⊙P与平行四边形ABCD的边有三个公共点,随着AP的变化,⊙P与平行四边形ABCD的边的公共点的个数也在变化,若公共点的个数为4,直接写出相对应的AP的值的取值范围 <AP<或AP=5 .
【分析】(1)在Rt△ABC中,直接由勾股定理可求出结果;
(2)连接PF,则PF⊥CD,由AB⊥AC和四边形ABCD是平行四边形,得PF∥AC,可证明△DPF∽△DAC,列比例式可得AP的长;
(3)有两种情况:①与边AD、CD分别有两个公共点;②⊙P过点A、C、D三点,可分别写出结论.
【解答】解:(1)∵平行四边形ABCD中,AB=6,AD=10,
∴BC=AD=10,
∵AB⊥AC,
∴在Rt△ABC中,由勾股定理得:AC===8,
故答案为:8;
(2)如图2所示,连接PF,
设AP=x,则DP=10﹣x,PF=x,
∵⊙P与边CD相切于点F,
∴PF⊥CD,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∵AB⊥AC,
∴AC⊥CD,
∴AC∥PF,
∴△DPF∽△DAC,
∴=,
∴=,
∴x=,
即AP=;
(3)当⊙P与BC相切时,设切点为G,如图3,
S▱ABCD=×6×8×2=10PG,
∴PG=,
①当⊙P与边AD、CD分别有两个公共点时,<AP<,即此时⊙P与平行四边形ABCD的边的公共点的个数为4;
②⊙P过点A、C、D三点,如图4,⊙P与平行四边形ABCD的边的公共点的个数为4,此时AP=5,
综上所述,AP的值的取值范围是:<AP<或AP=5,
故答案为:<AP<或AP=5.
【点评】本题是圆与平行四边形的综合题,考查了圆的切线的性质、勾股定理、平行四边形性质和面积公式,第2问注意利用分类讨论的思想,并利用数形结合解决问题.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
日期:2020/10/24 9:02:48;用户:钱军华;邮箱:sjhzxyh09@xyh.com;学号:37801999
一.选择题(本大题共16小题,共42分.1-10小题各3分,11-16小题各2分,小题给出的四个选项中,只有一项是符合题目要求的)
1.(3分)sin30°的值为( )
A. B. C. D.
2.(3分)方程(x﹣2)2=0的根是( )
A.2 B.﹣2 C.0 D.无解
3.(3分)函数y=,当x>0时的图象为( )
A. B.
C. D.
4.(3分)如图,在△ABC中,DE∥BC,若,则AE:AC等于( )
A.3:2 B.2:3 C.4:9 D.1:2
5.(3分)如图,在⊙O中,点A是的中点,∠AOB=40°,则∠ADC的度数是( )
A.15° B.20° C.25° D.40°
6.(3分)在同一平面内,过已知A、B、C三个点可以作圆的个数为( )
A.0个 B.1个 C.2个 D.0个或1个
7.(3分)某超市一月份的营业额为200万元,第一季度的营业额1000万元,如果平均每月增长率为x元,则由题意列方程应为( )
A.200(1+x)2=1000
B.200+200•2•x=1000
C.200+200•3•x=1000
D.200[1+(1+x)+(1+x)2]=1000
8.(3分)如图,在平面直角坐标系中,以原点O为位似中心,将△ABO扩大到原来的2倍,得到对应的△A′B′O.若点B的坐标是(﹣2,1),则点B′的坐标是( )
A.(4,﹣2) B.(﹣4,2) C.(2,﹣4) D.(﹣2,4)
9.(3分)a,b是实数,点A(4,a)、B(5,b)在反比例函数y=的图象上,则( )
A.a<b<0 B.b<a<0 C.a<0<b D.b<0<a
10.(3分)若⊙P的半径为5,圆心P的坐标为(﹣3,4),则平面直角坐标系的原点O与⊙P的位置关系是( )
A.在⊙P内 B.在⊙P上 C.在⊙P外 D.无法确定
11.(2分)若关于x的方程x2﹣x+sina=0有两个相等的实数根,则锐角a为( )
A.75° B.60° C.45° D.30°
12.(2分)已知圆锥的底面半径为5cm,母线长为13cm,则这个圆锥的侧面积是( )
A.60πcm2 B.65πcm2 C.120πcm2 D.130πcm2
13.(2分)如图,三角形纸片ABC的周长为22cm,BC=6cm,⊙O是△ABC的内切圆,玲玲用剪刀在⊙O的左侧沿着与⊙O相切的任意一条直线MN剪下一个△AMN,则△AMN的周长是( )
A.10cm B.12cm
C.14cm D.根据MN位置不同而变化
14.(2分)如图,点A在反比例函数y=(x>0)的图象上,过点A作AB⊥x轴,垂足为点B,点C在y轴上,则△ABC的面积为( )
A.3 B.2 C. D.1
15.(2分)如图,定点C、动点D在⊙O上,并且位于直径AB的两侧,AB=5,AC=3,过点C在作CE⊥CD交DB的延长线于点E,则线段CE长度的最大值为( )
A.5 B.8 C. D.
16.(2分)如图,已知函数y=﹣3x与y=的图象在第二象限交于点A(m,y1),点B(m﹣1,y2)在y=的图象上,且点B在以O点为圆心,OA为半径的⊙O上,则k的值为( )
A.﹣ B.﹣1 C.﹣ D.﹣2
二.填空题(本大题共3小题,共11分.17小题3分;18-19小题各有2个空,每个空2分.把答案写在答题卡相应题号中的横线上)
17.(3分)如图,某游乐场一山顶滑梯的高为h,滑梯的坡角为α,那么滑梯长l为 .
18.(3分)已知正六边形的边长为2,则它的内切圆的半径是 ,扇形AOB的面积 .
19.(4分)如图,在矩形ABCD中,AB=4,AD=6,E是AB边的中点,F是线段BC上的动点,将△EBF沿EF所在直线折叠得到△EB′F,连接ED,则DE的长度是 ,B′D的最小值是 .
三.解答题(本大题共7小题,共67分.解答应写出文字说明、证明过程或演算步骤)
20.(8分)(1)解方程:x(x﹣1)=2;
(2)(1﹣sin45°)0﹣tan60°+.
21.(9分)如图,在Rt△AOB中,∠ABO=90°,OB=4,AB=8,且反比例函数y=在第一象限内的图象分别交OA,AB于点C和点D,连结OD,△BOD的面积是4.
(1)求反比例函数解析式;
(2)将△AOB沿x轴向左运动,运动速度是每秒钟3个单位长度,求△AOB与反比例函数图象没有交点时,运动时间t的取值范围.
22.(10分)已知,如图,==,那么△ABD与△BCE相似吗?为什么?
23.(9分)如图,学校打算用16m的篱笆围成一个长方形的生物园饲养小兔,生物园的一面靠墙(如图),面积是30m2.求生物园的长和宽.
24.(10分)为了计算湖中小岛上凉亭P到岸边公路l的距离,某数学兴趣小组在公路l上的点A处,测得凉亭P在北偏东60°的方向上;从A处向正东方向行走200米,到达公路l上的点B处,再次测得凉亭P在北偏东45°的方向上,如图所示.求凉亭P到公路l的距离.(结果保留整数,参考数据:≈1.414,≈1.732)
25.(10分)如图,PA是⊙O的切线,切点为A,AC是⊙O的直径,连接OP交⊙O于E.过A点作AB⊥PO于点D,交⊙O于B,连接BC,PB.
(1)求证:PB是⊙O的切线;
(2)求证:E为△PAB的内心;
(3)若cos∠PAB=,BC=1,求PO的长.
26.(12分)如图1,平行四边形ABCD中,AB⊥AC,AB=6,AD=10,点P在边AD上运动,以P为圆心,PA为半径的⊙P与对角线AC交于A,E两点.
(1)线段AC的长度是 .
(2)如图2,当⊙P与边CD相切于点F时,求AP的长;
(3)不难发现,当⊙P与边CD相切时,⊙P与平行四边形ABCD的边有三个公共点,随着AP的变化,⊙P与平行四边形ABCD的边的公共点的个数也在变化,若公共点的个数为4,直接写出相对应的AP的值的取值范围 .
2019-2020学年河北省石家庄十七中九年级(上)期中数学试卷
参考答案与试题解析
一.选择题(本大题共16小题,共42分.1-10小题各3分,11-16小题各2分,小题给出的四个选项中,只有一项是符合题目要求的)
1.(3分)sin30°的值为( )
A. B. C. D.
【分析】根据特殊角三角函数值,可得答案.
【解答】解:sin30°=,
故选:A.
【点评】本题考查了特殊角三角函数值,熟记特殊角三角函数值是解题关键.
2.(3分)方程(x﹣2)2=0的根是( )
A.2 B.﹣2 C.0 D.无解
【分析】根据直接开方法即可求出答案
【解答】解:∵(x﹣2)2=0,
∴x1=x2=2,
故选:A.
【点评】本题考查一元二次方程,解题的关键是熟练运用一元二次方程的解法,本题属于基础题型.
3.(3分)函数y=,当x>0时的图象为( )
A. B.
C. D.
【分析】根据反比例函数的比例系数可得图象在二或四象限,根据自变量的取值可得图象的准确象限.
【解答】解:∵反比例函数的比例系数为﹣4,
∴反比例函数的图象在第二、四象限,
∵x>0,
∴图象在第四象限,
故选:B.
【点评】考查反比例函数的性质;用到的知识点为:反比例函数的比例系数为负数,图象在二四象限;第四象限点的坐标的符号为(+,﹣).
4.(3分)如图,在△ABC中,DE∥BC,若,则AE:AC等于( )
A.3:2 B.2:3 C.4:9 D.1:2
【分析】由DE∥CB,根据平行线分线段成比例定理,可求得AE、AC的比例关系.
【解答】解:∵DE∥BC,AD:DB=2:3,
∴AE:AC=2:3.
故选:B.
【点评】此题主要考查了平行线分线段成比例定理,根据已知得出AE与EC的关系是解题关键.
5.(3分)如图,在⊙O中,点A是的中点,∠AOB=40°,则∠ADC的度数是( )
A.15° B.20° C.25° D.40°
【分析】直接利用圆周角求解.
【解答】解:∵点A是的中点,
∴=,
∴∠ADC=∠AOB=×40°=20°.
故选:B.
【点评】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
6.(3分)在同一平面内,过已知A、B、C三个点可以作圆的个数为( )
A.0个 B.1个 C.2个 D.0个或1个
【分析】分两种情况讨论:①A、B、C三个点共线,不能做圆;②A、B、C三个点不在同一条直线上,有且只有一个圆.
【解答】解:当A、B、C三个点共线,过A、B、C三个点不能作圆;
当A、B、C不在同一条直线上,过A、B、C三个点的圆有且只有一个,即三角形的外接圆;
故选:D.
【点评】本题考查了确定圆的条件,注:过三点作圆,分两种情况:①三点共线;②三点不共线.
7.(3分)某超市一月份的营业额为200万元,第一季度的营业额1000万元,如果平均每月增长率为x元,则由题意列方程应为( )
A.200(1+x)2=1000
B.200+200•2•x=1000
C.200+200•3•x=1000
D.200[1+(1+x)+(1+x)2]=1000
【分析】根据题意可以列出相应的方程,本题得以解决.
【解答】解:由题意可得,
200+200(1+x)+200(1+x)2=1000,
200[1+(1+x)+(1+x)2]=1000,
故选:D.
【点评】本题考查由实际问题抽象出一元二次方程,解题的关键是明确题意,列出相应的方程.
8.(3分)如图,在平面直角坐标系中,以原点O为位似中心,将△ABO扩大到原来的2倍,得到对应的△A′B′O.若点B的坐标是(﹣2,1),则点B′的坐标是( )
A.(4,﹣2) B.(﹣4,2) C.(2,﹣4) D.(﹣2,4)
【分析】根据以原点O为位似中心,将△ABO扩大到原来的2倍,即可得出对应点的坐标应乘以﹣2,即可得出点B′的坐标.
【解答】解:根据以原点O为位似中心,图形的坐标特点得出,对应点的坐标应乘以﹣2,
故点B的坐标是(﹣2,1),则点B′的坐标是(4,﹣2),
故选:A.
【点评】此题主要考查了关于原点对称的位似图形的性质,得出对应点的坐标乘以k或﹣k是解题关键.
9.(3分)a,b是实数,点A(4,a)、B(5,b)在反比例函数y=的图象上,则( )
A.a<b<0 B.b<a<0 C.a<0<b D.b<0<a
【分析】由k=﹣3<0,可得到图象位于二、四象限,y随x的增大而增大,再由A(4,a)、B(5,b)两点横坐标的大小判断出a、b,再由图象的位置进而判断出a、b、0,之间的关系.
【解答】解:∵k=﹣3<0,
∴图象位于二、四象限,在每个象限内,y随x的增大而增大,
∴点A(4,a)、B(5,b)在第四象限内图象上的两点,
∴a<b<0,
故选:A.
【点评】考查反比例函数的图象和性质,掌握反比例函数的图象和性质是正确判断的前提,利用图象法则会更直观.
10.(3分)若⊙P的半径为5,圆心P的坐标为(﹣3,4),则平面直角坐标系的原点O与⊙P的位置关系是( )
A.在⊙P内 B.在⊙P上 C.在⊙P外 D.无法确定
【分析】由勾股定理等性质算出点与圆心的距离d,则d>r时,点在圆外;当d=r时,点在圆上;当d<r时,点在圆内.
【解答】解:由勾股定理,得
OP==5,
d=r=5,
原点O在⊙P上.
故选:B.
【点评】本题考查了对点与圆的位置关系的判断.关键要记住若半径为r,点到圆心的距离为d,则有:当d>r时,点在圆外;当d=r时,点在圆上,当d<r时,点在圆内.
11.(2分)若关于x的方程x2﹣x+sina=0有两个相等的实数根,则锐角a为( )
A.75° B.60° C.45° D.30°
【分析】根据判别式的意义得到△=(﹣)2﹣4sinα=0,从而可求出α的正弦值,然后根据特殊角的三角函数值确定α的度数.
【解答】解:根据题意得△=(﹣)2﹣4sinα=0,
解得sinα=,
所以锐角α=30°.
故选:D.
【点评】本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2﹣4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.也考查了特殊角的三角函数值.
12.(2分)已知圆锥的底面半径为5cm,母线长为13cm,则这个圆锥的侧面积是( )
A.60πcm2 B.65πcm2 C.120πcm2 D.130πcm2
【分析】利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形面积公式计算.
【解答】解:这个圆锥的侧面积=×2π×5×13=65π(cm2).
故选:B.
【点评】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.
13.(2分)如图,三角形纸片ABC的周长为22cm,BC=6cm,⊙O是△ABC的内切圆,玲玲用剪刀在⊙O的左侧沿着与⊙O相切的任意一条直线MN剪下一个△AMN,则△AMN的周长是( )
A.10cm B.12cm
C.14cm D.根据MN位置不同而变化
【分析】设E,F,G,H分别是直线AC,AB,MN,BC与⊙O的切点.根据△AMN的周长=AM+AN+MG+NF=AM+ME+AN+NF=AE+AF,想办法求出AE+AF即可解决问题.
【解答】解:设E,F,G,H分别是直线AC,AB,MN,BC与⊙O的切点.
由切线长定理可知:CE=CH,BH=BF.ME=MG,NG=NF,
∵AC+AB+BC=22cm,BC=6cm,
∴AC+AB=16cm,AE+AF=10cm,
∴△AMN的周长=AM+AN+MG+NF=AM+ME+AN+NF=AE+AF=10cm,
故选:A.
【点评】本题考查三角形的内切圆与内心,切线长定理等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
14.(2分)如图,点A在反比例函数y=(x>0)的图象上,过点A作AB⊥x轴,垂足为点B,点C在y轴上,则△ABC的面积为( )
A.3 B.2 C. D.1
【分析】连结OA,如图,利用三角形面积公式得到S△OAB=S△CAB,再根据反比例函数的比例系数k的几何意义得到S△OAB=|k|,便可求得结果.
【解答】解:连结OA,如图,
∵AB⊥x轴,
∴OC∥AB,
∴S△OAB=S△CAB,
而S△OAB=|k|=,
∴S△CAB=,
故选:C.
【点评】本题考查了反比例函数的比例系数k的几何意义:在反比例函数y=图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.
15.(2分)如图,定点C、动点D在⊙O上,并且位于直径AB的两侧,AB=5,AC=3,过点C在作CE⊥CD交DB的延长线于点E,则线段CE长度的最大值为( )
A.5 B.8 C. D.
【分析】当CD是直径时,CE最长,由AB是直径,得到∠ACB=90°,利用勾股定理得出BC的长度,又因为∠A=∠D,∠ABC=∠ACE=90°,推出△ABC∽△DCE,根据相似三角形的性质列方程求解.
【解答】解:当CD是直径时,CE最长,
∵AB是直径,
∴∠ACB=90°,
∴BC=,
∵∠A=∠D,∠ABC=∠ACE=90°,
∴△ABC∽△DCE,
∴,
即,
∴CE=,
故选:D.
【点评】本题考查了相似三角形的判定和性质,圆周角定理,解直角三角形,勾股定理的应用,确定CE什么时候取最大值是解题的关键.
16.(2分)如图,已知函数y=﹣3x与y=的图象在第二象限交于点A(m,y1),点B(m﹣1,y2)在y=的图象上,且点B在以O点为圆心,OA为半径的⊙O上,则k的值为( )
A.﹣ B.﹣1 C.﹣ D.﹣2
【分析】由题意A(m,﹣3m),因为⊙O与反比例函数y=都是关于直线y=﹣x对称,推出A与B关于直线y=﹣x对称,推出B(3m,﹣m),可得3m=m﹣1,求出m即可解决问题;
【解答】解:∵函数y=﹣3x与y=的图象在第二象限交于点A(m,y1),
∴点A(m,﹣3m)
∵∵⊙O与反比例函数y=都是关于直线y=﹣x对称,
∴A与B关于直线y=﹣x对称,
∴B(3m,﹣m),
∴3m=m﹣1,
∴m=﹣
∴点A(﹣,)
∴k=﹣×=﹣
故选:A.
【点评】本题考查反比例函数与一次函数的交点问题,解题的关键是灵活运用所学知识解决问题,本题的突破点是发现A,B关于直线y=﹣x对称.
二.填空题(本大题共3小题,共11分.17小题3分;18-19小题各有2个空,每个空2分.把答案写在答题卡相应题号中的横线上)
17.(3分)如图,某游乐场一山顶滑梯的高为h,滑梯的坡角为α,那么滑梯长l为 .
【分析】根据三角函数的定义即可求解.
【解答】解:∵sina=,
∴l=.
故答案为:.
【点评】本题考查了解直角三角形﹣坡度与坡角,三角函数的定义,理解定义是关键.
18.(3分)已知正六边形的边长为2,则它的内切圆的半径是 ,扇形AOB的面积 .
【分析】根据题意画出图形,利用正六边形中的等边三角形的性质求解即可.
【解答】解:如图,连接OA、OB,OG;
∵六边形ABCDEF是边长为2的正六边形,
∴△OAB是等边三角形,
∴OA=AB=2,
∴OG=OA•sin60°=2×=,
∴边长为2的正六边形的内切圆的半径;
外接圆半径为2,扇形AOB的面积=,
故答案为,.
【点评】本题考查学生对正多边形的概念掌握和计算的能力.解答这类题往往一些学生因对正多边形的基本知识不明确,将多边形的半径与内切圆的半径相混淆而造成错误计算,记住基本概念是解题的关键,属于中考常考题型.
19.(4分)如图,在矩形ABCD中,AB=4,AD=6,E是AB边的中点,F是线段BC上的动点,将△EBF沿EF所在直线折叠得到△EB′F,连接ED,则DE的长度是 2 ,B′D的最小值是 2﹣2 .
【分析】根据翻折变换可得EB′=EB,∠EB′F=∠B=90°,E是AB边的中点,根据勾股定理可求解.
【解答】解:∵四边形ABCD是矩形,
∴∠A=∠B=90°,AD=6,AB=4,
∵E是AB边的中点,
∴AE=BE==2,
∴根据勾股定理,得
DE===2.
由折叠可知:
点B折叠后对应点B‘应是在以E为圆心,BE为半径的圆上运动,
所以DB'最小值应为B'在DE上时最小.
∴DB′的最小值为DE﹣BE=2﹣2.
故答案为2、2﹣2.
【点评】本题考查了翻折变换、矩形的性质,解决本题的关键是熟练运用翻折的性质.
三.解答题(本大题共7小题,共67分.解答应写出文字说明、证明过程或演算步骤)
20.(8分)(1)解方程:x(x﹣1)=2;
(2)(1﹣sin45°)0﹣tan60°+.
【分析】(1)整理后分解因式,即可得出两个一元一次方程,求出方程的解即可;
(2)先根据零指数幂,特殊角的三角函数值,算术平方根求出每一部分的值,再算加减即可.
【解答】解:(1)x(x﹣1)=2,
x2﹣x﹣2=0,
(x﹣2)(x+1)=0,
x﹣2=0,x+1=0,
x1=2,x2=﹣1;
(2)原式=1﹣+2
=3﹣.
【点评】本题考查了解一元二次方程,特殊角的三角函数值,零指数幂,算术平方根等知识点,能把一元二次方程转化成一元方程是解(1)的关键,能求出每一部分的值是解(2)的关键.
21.(9分)如图,在Rt△AOB中,∠ABO=90°,OB=4,AB=8,且反比例函数y=在第一象限内的图象分别交OA,AB于点C和点D,连结OD,△BOD的面积是4.
(1)求反比例函数解析式;
(2)将△AOB沿x轴向左运动,运动速度是每秒钟3个单位长度,求△AOB与反比例函数图象没有交点时,运动时间t的取值范围.
【分析】(1)根据反比例函数y=(k≠0)系数k的几何意义得到S△BOD=k=4,求出k即可确定反比例函数解析式;
(2)由反比例函数的性质即可判断A点在反比例函数的图象时t的值,即可得到t的取值范围.
【解答】解:(1)∵S△BOD=k,
∴k=4,解得k=8,
∴反比例函数解析式为y=;
(2)当A点移到反比例函数图象上,
∵AB=8,
∴A的纵坐标为8,
代入y=求得x=1,
此时A移到的距离为4﹣1=3,
∵3÷3=1,
∴t>1.
【点评】本题考查了反比例函数y=(k≠0)系数k的几何意义:从反比例函数y=kx(k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|.
22.(10分)已知,如图,==,那么△ABD与△BCE相似吗?为什么?
【分析】先根据三组对应边的比相等的两个三角形相似判断△ABC∽△DBE,得到∠ABC=∠DBE,则∠ABD=∠CBE,再利用比例性质由=得到=,于是根据两组对应边的比相等且夹角对应相等的两个三角形相似可判断△ABD∽△CBE.
【解答】解:∵==,
∴△ABC∽△DBE,
∴∠ABC=∠DBE,
∴∠ABC﹣∠DBC=∠DBE﹣∠DBC,
即∠ABD=∠CBE,
∵=,
∴=,
∴△ABD∽△CBE.
【点评】本题考查了相似三角形的判定:三组对应边的比相等的两个三角形相似;两组对应边的比相等且夹角对应相等的两个三角形相似.
23.(9分)如图,学校打算用16m的篱笆围成一个长方形的生物园饲养小兔,生物园的一面靠墙(如图),面积是30m2.求生物园的长和宽.
【分析】可设宽为x m,则长为(16﹣2x)m,根据等量关系:面积是30m2.列出方程求解即可.
【解答】解:设宽为x m,则长为(16﹣2x)m.
由题意,得 x•(16﹣2x)=30,
解得 x1=3,x2=5.
当x=3时,16﹣2×3=10,
当x=5时,16﹣2×5=6.
答:围成矩形的长为10 m、宽为3 m,或长为6 m、宽为5m.
【点评】考查了一元二次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.
24.(10分)为了计算湖中小岛上凉亭P到岸边公路l的距离,某数学兴趣小组在公路l上的点A处,测得凉亭P在北偏东60°的方向上;从A处向正东方向行走200米,到达公路l上的点B处,再次测得凉亭P在北偏东45°的方向上,如图所示.求凉亭P到公路l的距离.(结果保留整数,参考数据:≈1.414,≈1.732)
【分析】作PD⊥AB于D,构造出Rt△APD与Rt△BPD,根据AB的长度.利用特殊角的三角函数值求解.
【解答】解:作PD⊥AB于D.
设BD=x,则AD=x+200.
∵∠EAP=60°,
∴∠PAB=90°﹣60°=30°.
在Rt△BPD中,
∵∠FBP=45°,
∴∠PBD=∠BPD=45°,
∴PD=DB=x.
在Rt△APD中,
∵∠PAB=30°,
∴PD=tan30°•AD,
即DB=PD=tan30°•AD,
可得:x=(200+x),
解得:x≈273.2,
∴PD≈273.
答:凉亭P到公路l的距离为273m.
【点评】此题考查的是直角三角形的性质,解答此题的关键是构造出两个特殊角度的直角三角形,再利用特殊角的三角函数值解答.
25.(10分)如图,PA是⊙O的切线,切点为A,AC是⊙O的直径,连接OP交⊙O于E.过A点作AB⊥PO于点D,交⊙O于B,连接BC,PB.
(1)求证:PB是⊙O的切线;
(2)求证:E为△PAB的内心;
(3)若cos∠PAB=,BC=1,求PO的长.
【分析】(1)连结OB,根据圆周角定理得到∠ABC=90°,证明△AOP≌△BOP,得到∠OBP=∠OAP,根据切线的判定定理证明;
(2)连结AE,根据切线的性质定理得到∠PAE+∠OAE=90°,证明EA平分∠PAD,根据三角形的内心的概念证明即可;
(3)根据余弦的定义求出OA,证明△PAO∽△ABC,根据相似三角形的性质列出比例式,计算即可.
【解答】(1)证明:连结OB,
∵AC为⊙O的直径,
∴∠ABC=90°,
∵AB⊥PO,
∴PO∥BC
∴∠AOP=∠C,∠POB=∠OBC,
OB=OC,
∴∠OBC=∠C,
∴∠AOP=∠POB,
在△AOP和△BOP中,
,
∴△AOP≌△BOP(SAS),
∴∠OBP=∠OAP,
∵PA为⊙O的切线,
∴∠OAP=90°,
∴∠OBP=90°,
∴PB是⊙O的切线;
(2)证明:连结AE,
∵PA为⊙O的切线,
∴∠PAE+∠OAE=90°,
∵AD⊥ED,
∴∠EAD+∠AED=90°,
∵OE=OA,
∴∠OAE=∠AED,
∴∠PAE=∠DAE,即EA平分∠PAD,
∵PA、PB为⊙O的切线,
∴PD平分∠APB
∴E为△PAB的内心;
(3)解:∵∠PAB+∠BAC=90°,∠C+∠BAC=90°,
∴∠PAB=∠C,
∴cos∠C=cos∠PAB=,
在Rt△ABC中,cos∠C===,
∴AC=,AO=,
∵△PAO∽△ABC,
∴,
∴PO===5.
【点评】本题考查的是三角形的内切圆和内心、相似三角形的判定和性质、切线的判定,掌握切线的判定定理、相似三角形的判定定理和性质定理是解题的关键.
26.(12分)如图1,平行四边形ABCD中,AB⊥AC,AB=6,AD=10,点P在边AD上运动,以P为圆心,PA为半径的⊙P与对角线AC交于A,E两点.
(1)线段AC的长度是 8 .
(2)如图2,当⊙P与边CD相切于点F时,求AP的长;
(3)不难发现,当⊙P与边CD相切时,⊙P与平行四边形ABCD的边有三个公共点,随着AP的变化,⊙P与平行四边形ABCD的边的公共点的个数也在变化,若公共点的个数为4,直接写出相对应的AP的值的取值范围 <AP<或AP=5 .
【分析】(1)在Rt△ABC中,直接由勾股定理可求出结果;
(2)连接PF,则PF⊥CD,由AB⊥AC和四边形ABCD是平行四边形,得PF∥AC,可证明△DPF∽△DAC,列比例式可得AP的长;
(3)有两种情况:①与边AD、CD分别有两个公共点;②⊙P过点A、C、D三点,可分别写出结论.
【解答】解:(1)∵平行四边形ABCD中,AB=6,AD=10,
∴BC=AD=10,
∵AB⊥AC,
∴在Rt△ABC中,由勾股定理得:AC===8,
故答案为:8;
(2)如图2所示,连接PF,
设AP=x,则DP=10﹣x,PF=x,
∵⊙P与边CD相切于点F,
∴PF⊥CD,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∵AB⊥AC,
∴AC⊥CD,
∴AC∥PF,
∴△DPF∽△DAC,
∴=,
∴=,
∴x=,
即AP=;
(3)当⊙P与BC相切时,设切点为G,如图3,
S▱ABCD=×6×8×2=10PG,
∴PG=,
①当⊙P与边AD、CD分别有两个公共点时,<AP<,即此时⊙P与平行四边形ABCD的边的公共点的个数为4;
②⊙P过点A、C、D三点,如图4,⊙P与平行四边形ABCD的边的公共点的个数为4,此时AP=5,
综上所述,AP的值的取值范围是:<AP<或AP=5,
故答案为:<AP<或AP=5.
【点评】本题是圆与平行四边形的综合题,考查了圆的切线的性质、勾股定理、平行四边形性质和面积公式,第2问注意利用分类讨论的思想,并利用数形结合解决问题.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
日期:2020/10/24 9:02:48;用户:钱军华;邮箱:sjhzxyh09@xyh.com;学号:37801999
相关资料
更多








