



初中1 认识一元二次方程示范课课件ppt
展开对于前一课第一个问题,你能设法估计四周未铺地毯部分的宽度x ( m )吗?
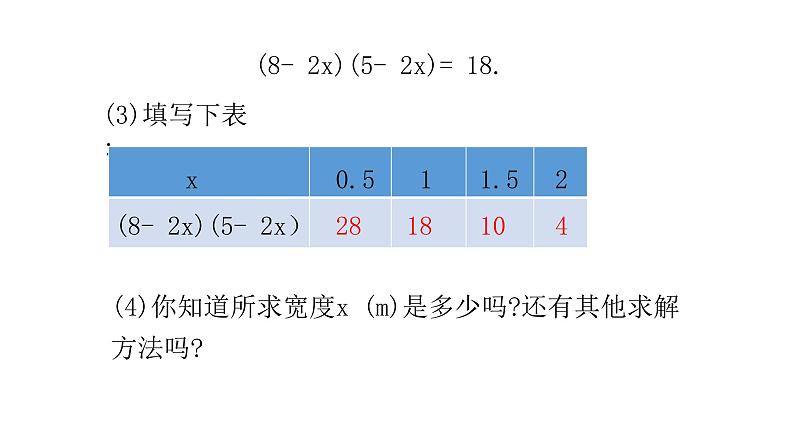
(8- 2x)(5- 2x)= 18.
(1) x可能小于0吗?可能大于4吗?可能大于2.5吗?说说你的理由.
(2)你能确定x的大致范围吗?
x不可能小于0,因为宽度不能为负
有可能大于4,负负得正
(8- 2x)(5- 2x)
(4)你知道所求宽度x (m)是多少吗?还有其他求解方法吗?
在前一课的问题中,梯子底端滑动的距离x (m)满足方程(x+6)2+72=102
也就是x2+12x-15=0.
(1)小明认为底端也滑动了1 m,他的说法正确吗?为什么?
(2)底端滑动的距离可能是2m吗?可能是3m吗?为什么?
因为方程左边不会等于0
不可能是2,也不可能是3,
(3)你能猜出滑动距离x (m)的大致范围吗?
(4) x的整数部分是几?十分位是几?
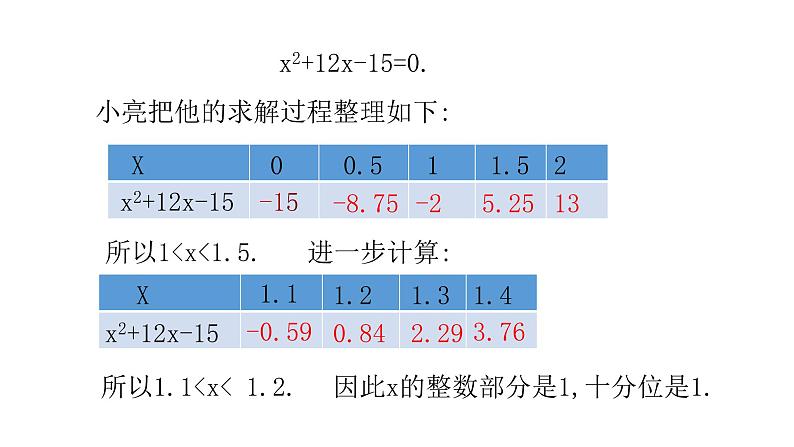
小亮把他的求解过程整理如下:
x2+12x-15=0.
所以1.1
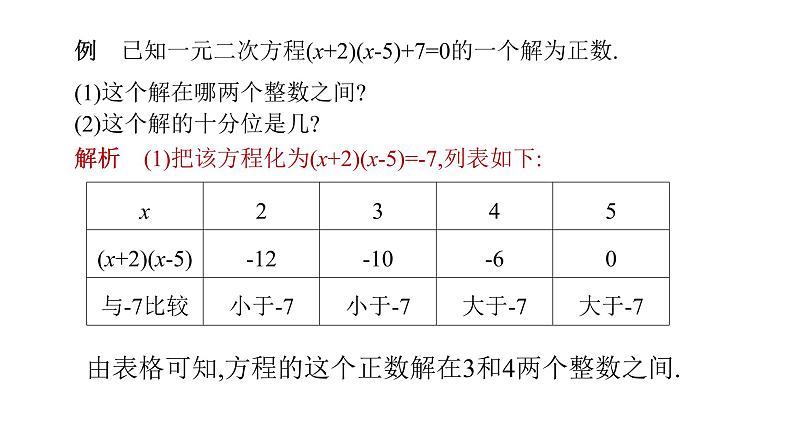
解析 (1)把该方程化为(x+2)(x-5)=-7,列表如下:
由表格可知,方程的这个正数解在3和4两个整数之间.
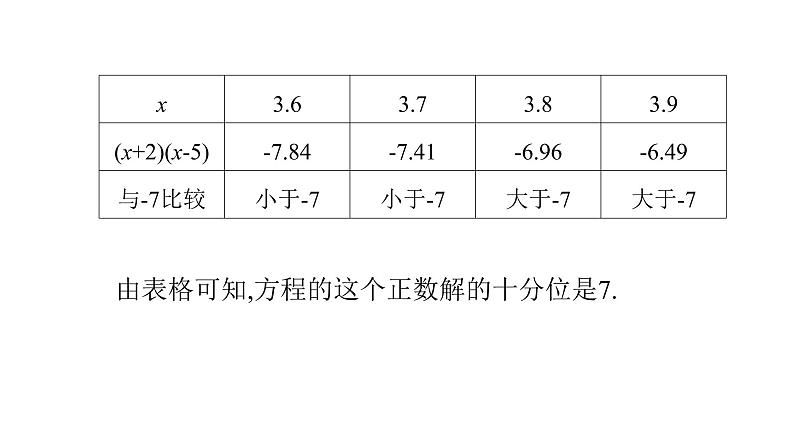
由表格可知,方程的这个正数解的十分位是7.
五个连续整数,前三个数的平方和等于后两个数的平方。您能求出这五个整数分别是多少吗?
设五个连续整数中的第一个数为x,那么后面四个数依次可表示为x+1,x+2,x+3,x+4.根据题意,可得方程:x2+(x+1)2+(x+2)2=(x+3)2+(x+4)2即:x2-8x-20=0
所以,x=-2或x=10
若设五个连续整数中的中间一个数为x,那么其余四个数依次可表示为x-2,x-1,x+1,x+2.根据题意,可得方程:(x-2)2+(x-1)2+x2=(x+1)2+(x+2)2即:x2-12x=0
所以,x=0或x=12
用二分法确定一元二次方程的近似解
本节课,我们通过不断缩小范围得到了一元二次方程的近似解。在数学学习和生产生活中,有很多这样通过缩小范围确定结果的例子。例如,估计、2的近似值,在某段线路上找出发生故障的那个点
缩小范围的常用方法是二分法.具体做法是:找出初始范围的中间点,判断解在中间点的哪一侧,得到一个新的范围,然后对这个新的范围进行类似操直到最终的结果符合实际问题的精确度要求。
比如,一个具体问题中,x满足方程(x-10)(x-20) =140,其中x> 20.
第一步:估计x的大致范围。根据题意,可知x>20,且x越大,方程左边的值就越大。不妨设x=30,可以算出此时方程左边的值是200,200> 140,因此可以确定20
可以看出,用二分法缩小范围时,操作过程是完全类似的,因此可以在计算机中借助程序进行“机械”操作.
不断重复第二步的操作,依次得到x的范围:
27.5
如图,设供电站和医院的所在处分别为点A、B
这样每查一次,就可以把待查的线路长度缩减一半,算一算,要把故障可能发生的范围缩小到50m~100m左右,即一两根电杆附近,大概要查多少次呢?
作业布置:习题2.2 1,2,3,4
1.若关于x的一元二次方程为ax2+bx+5=0(a≠0)的解是x=1,则2015-a-b的值是( ) A.2018 B.2008 C.2014 .2020
2.方程(m+2)x|m|+3mx+1=0是关于x的一元二次方程,则( )A.m = ±2 B.m = 2 C.m = -2 D.m≠±2
3.填写下表,并探索一元二次方程x2-6x+9=0的解的取值范围.从表上可以看出方程的解应介于 和 之间.4.根据下列表格中代数式ax2+bx+c与x的对应值,判断方程式ax2+bx+c=0(a≠0,a、b、c为常数)的一个根x的大致范围是( ) A.6<x<6.17 <x<6.18 <x<6.19 <x<6.20
5.下列关于x的一元二次方程(a-2)x2+x+a2-4=0的一个根是0,则a的值为( ) A.2 B.-2 C.2或-2 D.14
6.方程x2-2x-2=0的一较小根为x1,下面对x1的估计正确的是( ) A.-2<x1<-1 B.-1<x1<0 C.0<x1<1 D.1<x1<2
初中数学北师大版九年级上册1 认识一元二次方程试讲课ppt课件: 这是一份初中数学北师大版九年级上册1 认识一元二次方程试讲课ppt课件,文件包含21认识一元二次方程第2课时教学课件pptx、第二章一元二次方程21认识一元二次方程第2课时教案内含练习docx等2份课件配套教学资源,其中PPT共19页, 欢迎下载使用。
2021学年1 认识一元二次方程说课ppt课件: 这是一份2021学年1 认识一元二次方程说课ppt课件,共15页。
初中数学北师大版九年级上册1 认识一元二次方程集体备课ppt课件: 这是一份初中数学北师大版九年级上册1 认识一元二次方程集体备课ppt课件,共20页。PPT课件主要包含了课前展示,18m2,创境激趣,想一想,自学导航,做一做,合作探究,展示提升,强化训练,归纳总结等内容,欢迎下载使用。













